D2.2 Déterminer et comparer les probabilités théoriques et expérimentales que deux événements indépendants se produisent et que deux événements dépendants se produisent.
HABILETÉ : COMPARER DES PROBABILITÉS THÉORIQUES ET EXPÉRIMENTALES
Au cycle intermédiaire, les élèves apprennent à distinguer les événements indépendants et dépendants et à comparer la probabilité théorique et expérimentale que se produisent plusieurs de ces événements. Les élèves ont aussi recours à divers diagrammes pour déterminer la probabilité théorique de plus d’un événement.
Les expériences de probabilité sont essentielles au développement d’une bonne compréhension du concept de probabilité théorique. Ainsi, lorsque les élèves ont établi la probabilité théorique d’un résultat quelconque, le personnel enseignant peut leur proposer de vérifier cette probabilité de façon expérimentale. Cette activité leur permet aussi de mieux comprendre que l’incertitude est inhérente à toute situation liée au hasard; par exemple, même si elles et ils établissent que la probabilité théorique d’un résultat quelconque est égale à \(\frac{1}{4}\), rien ne garantit qu’elles et ils obtiendront ce résultat le quart des fois au cours d’une expérience.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 142.
La probabilité expérimentale montre que, si l’on effectue une expérience de probabilité suffisamment de fois et que l’on note la fréquence de chaque résultat, cette fréquence peut être utilisée pour déterminer une approximation de la probabilité théorique.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 151.
Pour acquérir une bonne compréhension du concept de probabilité théorique, les élèves doivent recourir à la fois à leur pensée intuitive et à leur pensée analytique. Il est donc important que le personnel enseignant leur présente des situations qui font appel à la théorie et à la pratique afin de favoriser un va-et-vient entre ces deux modes de pensée.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 138.
CONNAISSANCE : PROBABILITÉ THÉORIQUE
La probabilité théorique aide à quantifier le caractère aléatoire et incertain d’un événement ou d’un résultat. Cette quantité peut être représentée à l’aide d’une fraction située entre 0 et 1.
Exemple
Au jeu de pile ou face, la probabilité théorique d’obtenir le résultat pile est égale à \(\frac{1}{2}\). Cette fraction indique que le jeu comporte deux résultats équiprobables et qu’un de ces résultats est pile. Autrement dit, à ce jeu, on a 1 possibilité sur 2 d’obtenir le résultat pile.
Le personnel enseignant doit savoir que, si tous les résultats possibles d’une expérience sont équiprobables, la probabilité théorique d’un résultat A quelconque est définie de façon formelle comme suit.

Ainsi, si nous cherchons à déterminer la probabilité d’obtenir un nombre pair en lançant un dé à six faces, il suffit de reconnaître qu’il y a 6 résultats possibles (1, 2, 3, 4, 5 et 6) et que 3 de ces résultats correspondent à un nombre pair (2, 4 et 6). Nous pouvons donc dire que la probabilité théorique d’obtenir un nombre pair est égale à \(\frac{3}{6}\), c’est-à-dire qu’il y a 3 possibilités sur 6 que le résultat corresponde à un nombre pair. La notation P(A) est couramment employée pour décrire la probabilité d’un résultat A quelconque. Ainsi, dans la situation précédente, nous pourrions écrire P(nombre pair) \(=\frac{3}{6}\).
Dans certaines situations, un résultat souhaité peut ne jamais se produire; par exemple, obtenir un nombre supérieur à 6 en lançant le dé. La probabilité de ce résultat est donc égale à 0. Dans d’autres situations, il est certain que le résultat souhaité va se produire; par exemple, obtenir un nombre inférieur à 7 en lançant le dé. La probabilité de ce résultat est donc égale à 1.
La probabilité théorique nous aide à prendre des décisions réfléchies dans toute situation aléatoire. Puisque, dans de telles situations, il est impossible de prédire le résultat sans risquer de se tromper, nous pouvons diminuer ce risque en déterminant la probabilité théorique de chaque résultat et en choisissant le résultat dont la probabilité est la plus élevée. C’est, en quelque sorte, une façon de « mathématiser le hasard ».
La probabilité théorique est un concept mathématique abstrait qui n’est pas toujours facile à saisir. Cependant, sa compréhension est essentielle au développement de la pensée probabiliste. Afin que cette compréhension ne se résume pas à l’apprentissage d’une formule, elle doit être le fruit d’un long processus au cours duquel le personnel enseignant expose les élèves à diverses situations, jeux ou expériences de probabilité qui les aident à confronter la théorie et la pratique. Cette approche crée souvent un déséquilibre chez celles et ceux qui, devant une situation particulière, se laissent mener par leur intuition ou par une analyse fautive. Même chez les adultes, il est très fréquent de mal analyser une situation aléatoire d’apparence simple.
Développement du concept de probabilité théorique
Au cycle moyen, les élèves acquièrent graduellement une compréhension du concept de probabilité théorique. En 4e année, par exemple, elles et ils peuvent affirmer qu’il y a 1 possibilité sur 6 d’obtenir le nombre 4 en lançant un dé. En 5e année, elles et ils apprennent à exprimer cette probabilité à l’aide d’une fraction, soit \(\frac{1}{6}\). En 6e année, elles et ils peuvent aussi utiliser un nombre décimal ou un pourcentage pour représenter la probabilité d’un résultat. En 7e année, les élèves apprennent à distinguer des événements indépendants d’événements dépendants en expliquant pourquoi leurs probabilités respectives diffèrent.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 137-139.
Note : Si nous connaissons la probabilité théorique d’un résultat quelconque d’une expérience, la Loi des grands nombres stipule que, plus nous faisons l’expérience souvent, plus le rapport entre la fréquence du résultat et le nombre d’essais se rapprochera de la probabilité théorique.
Raisonnement proportionnel
Il y a un lien important entre la pensée probabiliste et le raisonnement proportionnel. Le raisonnement proportionnel aide à reconnaître la relation d’équivalence entre deux situations de probabilité, contribuant ainsi à la compréhension du concept de probabilité théorique. Le personnel enseignant doit proposer aux élèves diverses activités qui les incitent à établir ce lien.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 143-144.
Exemple 1 : deux événements indépendants
Présenter aux élèves la situation suivante :
Véronique aimerait faire une activité avec une de ses amies. Elle hésite entre demander à Astryde, à Hakima, à Sophie ou à Inès, et elle hésite entre aller au parc, faire du vélo ou aller à la piscine. Si elle décide de choisir l’amie et l’activité au hasard, quelle est la probabilité que Véronique :
- se rende à la piscine avec Hakima?
- fasse une activité avec Inès?
- fasse du vélo?
Les élèves peuvent dessiner deux roulettes pour mieux visualiser la situation.

Lorsque nous faisons tourner les deux flèches, nous nous intéressons à la probabilité des résultats combinés. Il faut d’abord déterminer et énumérer les résultats équiprobables possibles. Si la première flèche s’arrête sur le nom Astryde, la seconde flèche peut s’arrêter sur l’activité Parc, Vélo ou Piscine. La même chose se produit si la première flèche s’arrête sur le nom Hakima, Sophie ou Inès. Il y a donc 12 résultats équiprobables qui peuvent être représentés :
- à l’aide d’un diagramme en arbre;

- à l’aide d’un tableau;
| Vélo | Parc | Piscine | |
|---|---|---|---|
| Astryde | Vélo avec Astryde | Parc avec Astryde | Piscine avec Astryde |
| Hakima | Vélo avec Hakima | Parc avec Hakima | Piscine avec Hakima |
| Sophie | Vélo avec Sophie | Parc avec Sophie | Piscine avec Sophie |
| Inès | Vélo avec Inès | Parc avec Inès | Piscine avec Inès |
- à l’aide d’une liste ordonnée.
- Astryde et vélo, parc, piscine
- Hakima et vélo, parc, piscine
- Sophie et vélo, parc, piscine
- Inès et vélo, parc, piscine.
ou
- Vélo avec Astryde, Hakima, Sophie ou Inès
- Parc avec Astryde, Hakima, Sophie ou Inès
- Piscine avec Astryde, Hakima, Sophie ou Inès
Peu importe la représentation utilisée, les élèves peuvent ensuite voir qu’il y a 1 seul résultat parmi les 12 résultats équiprobables possibles qui correspond à la sortie à la piscine avec Hakima. La probabilité que Véronique se rende à la piscine avec Hakima est donc égale à \(\frac{1}{12}\). Pour répondre aux deux autres questions, les élèves peuvent se référer aux 12 résultats possibles ou uniquement à la roulette correspondant à la question. Ainsi, la probabilité que Véronique fasse une activité avec Inès est égale à \(\frac{3}{12}\) ou \(\frac{1}{4}\). La probabilité qu’elle fasse du vélo est égale à \(\frac{4}{12}\) ou \(\frac{1}{3}\).
Après avoir déterminé ces probabilités, les élèves peuvent réaliser une expérience de probabilité pour vérifier la vraisemblance de leurs réponses en utilisant deux roulettes comme celles présentées ci-dessus. Elles et ils peuvent aussi mettre quatre jetons de couleur différente dans un premier sac et trois jetons de couleur différente dans un second sac. Chaque jeton du premier sac est associé à une des quatre amies et chaque jeton du second sac est associé à une des trois activités. L’expérience consiste alors à tirer un jeton de chaque sac et à noter les résultats. Le personnel enseignant doit rappeler aux élèves l’importance d’effectuer l’expérience un nombre de fois suffisant.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 145-147.
Exemple 2 : deux événements dépendants
Présenter aux élèves un sac contenant une bille rouge, une bille verte et une bille bleue. La situation consiste à tirer, à deux reprises, une bille du sac et à noter sa couleur. Entre les deux tirages, la bille ne doit pas être remise dans le sac. Demander aux élèves de déterminer la probabilité d’obtenir :
- deux billes rouges;
- une bille rouge et une bille bleue;
- deux billes de couleur différente.
Pour résoudre ce problème, les élèves doivent énumérer l’ensemble des six résultats équiprobables possibles. Pour ce faire, elles et ils peuvent utiliser :
- un diagramme en arbre;
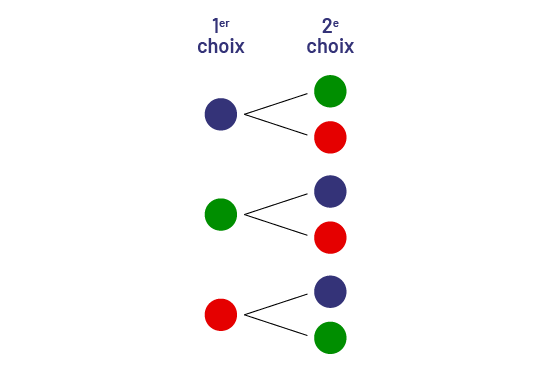
- un tableau;
| Bleue | Verte | Rouge | |
|---|---|---|---|
| Bleue | BV | BR | |
| Verte | VB | VR | |
| Rouge | RB | RV |
- une liste ordonnée.
- bleue, verte
- bleue, rouge
- verte, bleue
- verte, rouge
- rouge, bleue
- rouge, verte
En partant de ces résultats, les élèves peuvent déterminer que la probabilité d’obtenir :
- deux billes rouges est égale à 0;
- une bille rouge et une bille bleue est égale à \(\frac{2}{6}\);
- deux billes de couleur différente est égale à 1.
Les élèves devraient ensuite avoir l’occasion de vérifier la vraisemblance de leurs réponses en effectuant une expérience de probabilité.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 147-149.
CONNAISSANCE : PROBABILITÉ EXPÉRIMENTALE
La probabilité expérimentale est utilisée dans des situations où il est impossible de déterminer la probabilité théorique d’un événement ou d’un résultat en particulier.
Exemple
Les prévisions météorologiques, l’évaluation de l’espérance de vie ou la probabilité de réussir un lancer-franc au basketball.
L’apprentissage de la probabilité expérimentale devrait se faire dans le cadre de situations concrètes; par exemple, le personnel enseignant peut présenter diverses situations impliquant l’activité de tirer plusieurs objets d’un sac dont le contenu exact est inconnu. Il peut aussi présenter des situations où les résultats possibles ne sont pas nécessairement équiprobables. Sans compter qu’il peut présenter des situations dans lesquelles les résultats dépendent l’un de l’autre.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 150.
Exemple 1 : deux événements indépendants
Comparer les probabilités expérimentales avec les probabilités théoriques préalablement déterminées dans la situation suivante :
Véronique aimerait faire une activité avec une de ses amies. Elle hésite entre demander à Astryde, à Hakima, à Sophie ou à Inès, et elle hésite entre aller au parc, faire du vélo ou aller à la piscine. Si elle décide de choisir l’amie et l’activité au hasard, quelle est la probabilité que Véronique :
- se rende à la piscine avec Hakima?
- fasse une activité avec Inès?
- fasse du vélo?
Demander aux élèves d’effectuer l’expérience en utilisant des roulettes ou en utilisant un logiciel de codage par blocs :

En équipes de deux, les élèves font tourner la première roulette, puis la seconde, et notent leurs résultats dans un tableau. Après avoir effectué l’expérience 20 fois, elles et ils comparent leurs résultats avec les probabilités théoriques préalablement déterminées. Elles et ils peuvent noter en quoi leurs résultats diffèrent des résultats théoriques de se rendre à la piscine avec Hakima, de faire une activité avec Inès et de faire du vélo.
Les élèves découvrent que les résultats d’une expérience de probabilité peuvent être très différentes de ce que pourrait laisser croire la probabilité théorique. En effet, tous les résultats sont possibles, même ceux qui semblent peu probables.
Exemple 2 : deux événements dépendants
Comparer les probabilités expérimentales avec les probabilités théoriques préalablement déterminées dans la situation suivante :
Le personnel enseignant présente aux élèves un sac contenant une bille rouge, une bille verte et une bille bleue. La situation consiste à tirer, à deux reprises, une bille du sac et à noter sa couleur. Entre les deux tirages, la bille ne doit pas être remise dans le sac. Elle ou il leur demande de déterminer la probabilité d’obtenir :
- deux billes rouges;
- une bille rouge et une bille bleue;
- deux billes de couleur différente.
Demander aux élèves d’effectuer l’expérience en utilisant un sac brun et des billes rouges, vertes et bleues, ou en utilisant un logiciel de codage par blocs.
En équipes de deux, les élèves tirent une bille du sac, puis, sans remettre cette bille, tirent une deuxième bille du sac. Elles et ils notent leurs résultats dans un tableau. Après avoir effectué l’expérience 20 fois, elles et ils comparent leurs résultats avec les probabilités théoriques préalablement déterminées. Elles et ils peuvent noter en quoi leurs résultats diffèrent des résultats théoriques de tirer deux billes rouges, une bille rouge et une bille bleue et deux billes de couleur différente.
Les élèves découvrent que les résultats d’une expérience de probabilité peuvent être très différentes de ce que pourrait laisser croire la probabilité théorique. En effet, tous les résultats sont possibles, même ceux qui semblent peu probables.
Source : adapté de Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 145-149.
Événements indépendants et dépendants
Notons que, dans l’exemple 1, le résultat de la deuxième expérience ne dépend pas du résultat de la première. En mathématiques, on dit que ce sont des résultats indépendants. C’est là une autre occasion pour les élèves de comprendre l’idée que le hasard n’a pas de mémoire. L’exemple 2 est une situation d’expérience répétée où le résultat de la deuxième expérience dépend du résultat de la première. En mathématiques, on dit que ce sont des résultats dépendants. Si la bille est remise dans le sac à la suite du premier tirage, il y a trois résultats possibles au cours du deuxième tirage. Le nombre total de résultats équiprobables possibles serait ainsi 9. Cependant, puisque la bille n’est pas remise dans le sac à la suite du premier tirage, il ne reste que deux résultats possibles au cours du deuxième tirage. Le nombre total de résultats équiprobables possibles est ainsi 6.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 149.
