At a Glance...

F1.4 Determine the growth of simple and compound interest at various rates using digital tools, and explain the impact interest has on long-term financial planning.

Skill: Determining the Growth of Simple and Compound Interest at Various Rates

---

In any situation where interest is involved, there is money lent, and money borrowed, and the person or organization borrowing the money will have to pay interest on top of the original amount borrowed. There is, however, more than one way to calculate interest, each of which has advantages and disadvantages. The following two examples show borrowing and lending situations, and how both calculations of interest can be beneficial.

Example: Simple Interest

Borrowing to buy a car: When buying a car with a loan, interest is calculated at the outset and added to the principal amount, and this amount is divided by the number of payments.

For example, if a person borrows $1000 at an annual interest rate of 2% for 5 years, the interest is calculated at the beginning of the loan and divided by the number of payments. The person will spend a total of $1100: $1000 for the return of the original loan and $100 in interest ($1000 × 2% = $20 and $20 × 5 = $100).

Since simple interest does not take into account accrued interest (there is no interest calculated on the interest), simple interest has an advantage over compound interest for the person or organization borrowing the money (if the rates are comparable).

Example: Compound Interest

Guaranteed Investment Certificates (GICs): A GIC is a financial product that is like a loan to a financial institution from an individual. The individual agrees not to access a sum of money in exchange for a higher than usual interest rate. The interest is deposited in the current account, contributing to the account balance. This amount is then included in the interest calculation for the next payment. The principal investment and compound interest are paid to the individual at the end of the investment (maturity).

For example, if the individual commits to invest $1000 in a GIC at an annual interest rate of 2% for 5 years, the interest is always calculated from the account balance with accrued interest, each year as shown in the following table:

Since interest is calculated on the interest already paid, compound interest has an advantage over simple interest, for the person lending the money (when comparing two situations where the interest rates are comparable).

These examples could be modeled for the class by projecting or screen-sharing an online interest calculation tool. There are several available. Afterwards, students can use their own financial goals as inspiration to explore the online tools and see the effect of amount, term and interest rate on the value of a loan or investment.

Extensions: Compound interest can be represented by an exponential relationship, as shown in this graph:

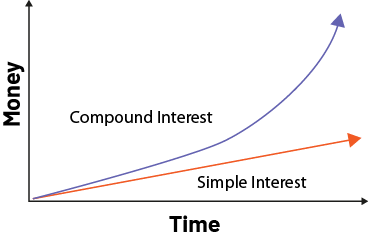
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Without presenting the actual formula for compound interest, which is still quite complex, using manipulatives or technology tools to create a graph like this one can demonstrate the growth of an investment or the value of a loan using both ways of calculating interest.

Example: Compound Interest (Exponential Relationship)

Example: Simple Interest (Linear Relationship)

Knowledge: Borrowing

---

Borrowing is receiving money with an agreement to repay it in future, usually with interest charged.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Knowledge: Simple Interests

---

Simple interest is always calculated on the same amount, that is, on the original amount.

Example

$5000 is invested at an annual rate of 6%; interest is paid at the end of the 3-year period:

Knowledge: Compound Interest

---

Interest calculated on the original principal of a deposit or loan, which takes into account all the accumulated interest from previous periods. Compound interest can be calculated on any schedule, either continuously, daily, or annually.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.

Example

$5000 invested at an annual rate of 6%; compound interest over 3 years:

Knowledge: Loan

---

A loan is an amount of money that is borrowed with the expectation that it will be paid back, usually with interest.

Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.