Fondements généraux du domaine Données
Cycle moyen
INTRODUCTION
« Il est artificiel de fragmenter l’enseignement du traitement des données et de la probabilité. […] Le défi est de créer des liens entre ces deux domaines. » [traduction libre]
(Shaughnessy, 2003, p. 216)
L’application des concepts de données et de probabilité est très fréquente dans notre quotidien. En effet, les journaux, les magazines, la radio, la télévision et Internet ont souvent recours aux diagrammes et aux données statistiques pour communiquer une information ou véhiculer un message; par exemple, des réclames publicitaires, des résultats sportifs, des sondages d’opinion, des tendances démographiques, une évaluation des risques pour la santé et des prévisions météorologiques.
Selon Burns (2000, p. 59-61), une connaissance appropriée des concepts de données et de probabilité est un atout dans la vie des élèves. Les élèves peuvent ainsi :
- se préparer à vivre dans une société de plus en plus axée sur les statistiques;
- éviter d’être induites et induits en erreur par les statistiques;
- développer leur habileté à raisonner;
- diminuer leur incertitude;
- rapporter fidèlement la réalité;
- dissiper certains préjugés;
- formuler convenablement leurs arguments;
- justifier leurs résultats à l’aide de données quantitatives.
Dans le programme-cadre de mathématiques, le traitement des données et la probabilité forment un même domaine. En effet, ces deux sujets sont indissociables, puisque, dans les deux cas, on recueille des données, on les organise, on les analyse et l’on en tire des conclusions. S’il est possible de traiter des données sans avoir recours aux probabilités, le contraire ne l’est pas toujours, les données étant essentielles au calcul des probabilités. Le personnel enseignant devrait donc privilégier une approche intégrée dans l’enseignement des concepts de données et de probabilité; par exemple, il peut demander aux élèves :
- de représenter les données recueillies au cours d’une enquête ou d’une expérience de probabilité au moyen d’un tableau ou d’un diagramme, et de les analyser;
- de communiquer leur interprétation des diagrammes en utilisant la terminologie appropriée;
- d’utiliser des données primaires ou secondaires pour répondre à une question d’intérêt, de formuler une conclusion ou de déterminer la probabilité d’un événement;
- d’exercer un jugement critique quant aux données recueillies, à leur représentation au moyen d’un diagramme et aux conclusions proposées.
Le traitement des données et la probabilité font habituellement partie de la branche des mathématiques appelée statistique. En statistique, un des principaux objectifs de l’enseignement est d’aider les élèves à analyser des données quantifiables et à prendre des décisions dans des situations impliquant la variabilité.
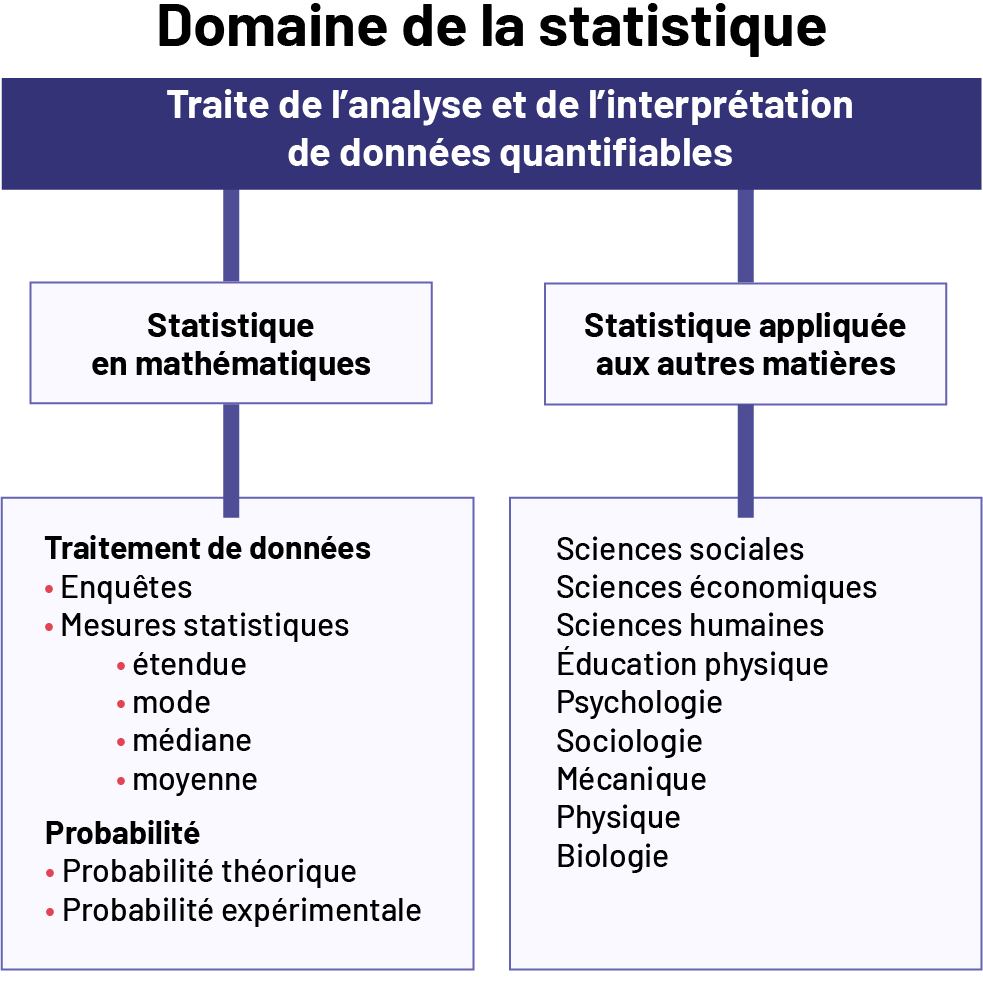 image Titre : Domaine de la statistique; Élément principal : Traite de l’analyse et de l’interprétation de données quantifiables. Deux éléments secondaires liés au premier : Statistique en mathématiques et Statistique appliquée aux autres matières; Sous Statistique en mathématiques : Traitement de données : Enquêtes, Mesures statistiques, étendue, mode, médiane, moyenne. Probabilité : Probabilité théorique, Probabilité expérimentale. Sous Statistique appliquée aux autres matières : Sciences sociales, Sciences économiques, Sciences humaines, Éducation physique, Psychologie, Sociologie, Mécanique, Physique, Biologie.
image Titre : Domaine de la statistique; Élément principal : Traite de l’analyse et de l’interprétation de données quantifiables. Deux éléments secondaires liés au premier : Statistique en mathématiques et Statistique appliquée aux autres matières; Sous Statistique en mathématiques : Traitement de données : Enquêtes, Mesures statistiques, étendue, mode, médiane, moyenne. Probabilité : Probabilité théorique, Probabilité expérimentale. Sous Statistique appliquée aux autres matières : Sciences sociales, Sciences économiques, Sciences humaines, Éducation physique, Psychologie, Sociologie, Mécanique, Physique, Biologie.
ENSEIGNEMENT EFFICACE DES DONNÉES ET DE LA PROBABILITÉ
L’enseignement du domaine Données au cycle moyen vise à accroître les compétences des élèves en matière de littératie statistique et à développer leur pensée probabiliste. Pour atteindre cet objectif, le personnel enseignant doit présenter aux élèves des situations d’apprentissage authentiques qui font appel au processus d’enquête et qui favorisent l’acquisition de certaines habiletés essentielles. Le schéma ci-dessous illustre l’interaction entre chacun de ces éléments.
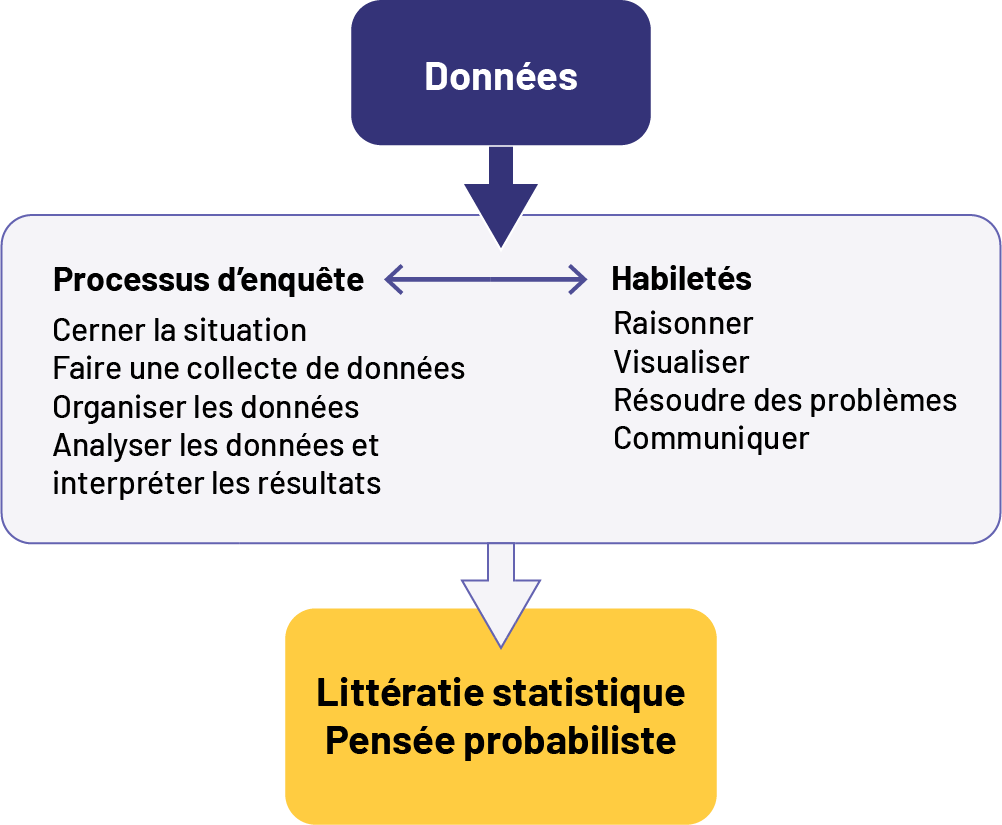 image Premier encadré : DonnéesFlèche pointant vers un autre encadré regroupant deux titres reliés par un droite avec une flèche à chaque extrémité : Processus d’enquête et HabiletésSous Processus d’enquête :Cerner la situationFaire une collecte de donnéesAnalyser les données et interpréter les résultatsSous Habiletés :Raisonner VisualiserRésoudre des problèmesCommuniquerFlèche qui part de cet encadré vers un autre encadré comprenant les titres suivants : Littératie statistiquePensée probabiliste
image Premier encadré : DonnéesFlèche pointant vers un autre encadré regroupant deux titres reliés par un droite avec une flèche à chaque extrémité : Processus d’enquête et HabiletésSous Processus d’enquête :Cerner la situationFaire une collecte de donnéesAnalyser les données et interpréter les résultatsSous Habiletés :Raisonner VisualiserRésoudre des problèmesCommuniquerFlèche qui part de cet encadré vers un autre encadré comprenant les titres suivants : Littératie statistiquePensée probabiliste
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 5-7.
Grandes idées du domaine Données
« Notre monde est de plus en plus centré sur la circulation de l’information, d’où l’importance croissante du domaine Données. Dès leur jeune âge, les enfants doivent savoir comment faire une collecte de données, utiliser ces renseignements pour comprendre leur monde et prendre des décisions qui ont des répercussions sur leur vie. » [traduction libre]
(Small, 2006, p. 1)
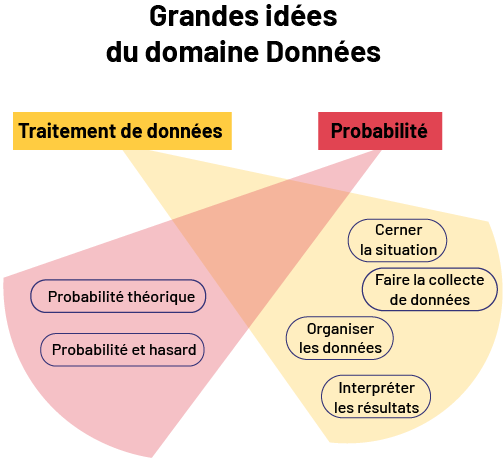 image Le schéma s’intitule « Grandes idées du domaine Données ». L’expression « Traitement de données » est surlignée en orange. À côté, le mot « Probabilité » est surligné de rouge. De chacun d’eux se déploie un faisceau lumineux de la même couleur. Dans le faisceau orange, les quatre expressions suivantes sont encerclées : « Cerner la situation. Faire la collecte de données. Organiser les données. Interpréter les résultats. » Dans le faisceau rouge, les deux expressions suivantes sont encerclées : « Probabilité théorique. Probabilité et hasard. »
image Le schéma s’intitule « Grandes idées du domaine Données ». L’expression « Traitement de données » est surlignée en orange. À côté, le mot « Probabilité » est surligné de rouge. De chacun d’eux se déploie un faisceau lumineux de la même couleur. Dans le faisceau orange, les quatre expressions suivantes sont encerclées : « Cerner la situation. Faire la collecte de données. Organiser les données. Interpréter les résultats. » Dans le faisceau rouge, les deux expressions suivantes sont encerclées : « Probabilité théorique. Probabilité et hasard. »
Aperçu
En mathématiques, le traitement des données et la probabilité forment un même domaine parce que leurs concepts sont liés et font appel aux mêmes habiletés; par exemple, les normes statistiques qui guident le choix de l’échantillon au cours d’un sondage sont fondées sur la probabilité, tout comme les modèles de probabilité théorique sont validés par les expériences de probabilité qui font appel à la collecte et au traitement des données.
Afin d’aider le personnel enseignant à définir et à prioriser les concepts clés de ce domaine, ainsi qu’à mettre en œuvre des stratégies d’enseignement efficaces, deux grandes idées sont proposées. Ces grandes idées renvoient directement aux deux principaux ensembles qui composent le domaine abordé, soit les données et la probabilité.
Grande idée 1 : Traitement des données
Les données permettent de développer les compétences en matière de littératie statistique.
Énoncé 1- Cerner la situation
Bien cerner une situation permet de formuler des questions d'intérêt pertinentes auxquelles on peut répondre en faisant une collecte et une analyse des données.
Énoncé 2 - Faire une collecte de données
La planification et la réalisation d'une collecte de données permettent de recueillir des données significatives.
Énoncé 3 - Organiser les données
L'organisation des données et leur représentation au moyen de tableaux et de diagrammes permettent de communiquer des renseignements en vue de leur interprétation.
Énoncé 4 - Interpréter les résultats
L'interprétation des résultats permet de tirer des conclusions pertinentes afin de répondre à des questions d'intérêt et de prendre des décisions réfléchies.
Grande idée 2 : Probabilité
La pensée probabiliste aide à prendre des décisions en tenant compte de l'incertitude découlant du hasard.
Énoncé 1 - Probabilité et hasard
La compréhension de la probabilité permet de traiter des situations liées au hasard.
Énoncé 2 - Probabilité théorique
L'analyse de données recueillies lors d'expériences aléatoires permet de mieux comprendre le concept de probabilité théorique.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 23-24.
Le processus d’enquête est une démarche de résolution de problèmes axée sur la collecte et l’analyse de données. Or, les données sont au cœur de toute réflexion liée à la littératie statistique et à la pensée probabiliste. Les élèves auront donc l’occasion de développer leurs compétences en matière de littératie statistique ainsi que leur pensée probabiliste dans la mesure où elles et ils seront exposés à diverses situations faisant appel au processus d’enquête.
Le texte ci-dessous résume les quatre étapes du processus d’enquête.
Étapes du processus d'enquête
- Cerner la situation
- Clarifier le problème.
- Formuler une ou plusieurs questions auxquelles on peut répondre en s'appuyant sur des données.
- Faire une collecte de données
- Élaborer un plan pour recueillir des données pertinentes et appropriées.
- Effectuer la collecte des données selon le plan et les enregistrer.
- Organiser les données
- Regrouper les données recueillies.
- Représenter les données de façon appropriée.
- Analyser les données et interpréter les résultats
- Comparer les données et les combiner.
- Attribuer un sens aux données.
Il est important de noter que ces étapes sont très semblables à celles du processus de résolution de problèmes. De plus, ces étapes ne signifient pas nécessairement que le processus est linéaire et séquentiel. En réalité, on va et vient d’une étape à l’autre, selon les besoins; par exemple, lorsqu’on interprète les résultats (étape 4) d’une enquête, présentés dans un tableau, on peut envisager qu’une représentation différente de ces résultats pourrait fournir de nouveaux renseignements. On peut alors revenir à l’étape de l’organisation des données (étape 3) et créer le diagramme en question. On peut même retourner à la question d’intérêt (étape 1) si l’on se rend compte qu’elle était imprécise ou que les résultats ne correspondent pas à l’intention initiale.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 11-12.
« L’utilisation de données authentiques liées à l’expérience personnelle des élèves les motive à apprendre, minimise les conceptions erronées, fonde la formulation d’inférences porteuses de sens et, conséquemment, assure une prise de décision réfléchie. » [traduction libre]
(Connor, Davies et Holmes, 2006, p. 185)
Raisonner, visualiser, résoudre une situation-problème et communiquer sont des habiletés étroitement liées au développement des compétences en matière de littératie statistique et au développement de la pensée probabiliste. Elles aident les élèves non seulement à recueillir et à organiser efficacement des données, ou à déterminer des probabilités, mais également à les comprendre et à les utiliser à bon escient. Le personnel enseignant doit donc continuellement chercher des occasions où les élèves pourront développer ces habiletés et les utiliser.
HABILETÉ À RAISONNER
L’habileté à raisonner aide les élèves à organiser leur pensée.
« En mathématiques, organiser signifie effectuer des activités mentales telles qu’abstraire, coordonner, différencier, intégrer, construire et structurer. »
(Ministère de l’Éducation du Québec, 2001, p. 128)
Dans le domaine Données, l’habileté à raisonner joue un rôle prépondérant à toutes les étapes du processus d’enquête. Le personnel enseignant peut, par son choix de questions, aider les élèves à développer cette habileté; par exemple, lorsque les élèves cherchent à cerner une situation donnée (étape 1), elle ou il peut les inciter à clarifier la situation et à réfléchir à la formulation d’une question d’intérêt appropriée. Au cours de l’étape de l’interprétation des résultats, elle ou il peut aussi les inciter à établir des liens entre les données et à lire au-delà des données.
L’habileté à raisonner est aussi très utilisée en probabilité. En effet, pour prendre des décisions réfléchies dans toute situation où les résultats varient de façon aléatoire, il est important de faire appel à la raison plutôt qu’à l’intuition. C’est là un des fondements de la pensée probabiliste; par exemple, si l’on obtient trois fois de suite un nombre pair lors de lancers d’un dé, notre intuition pourrait nous porter à croire que le prochain lancer donnera presque assurément un nombre impair. Or, en faisant appel à la raison, on constate que la probabilité d’obtenir un nombre pair au cours du quatrième lancer est égale à la probabilité d’obtenir un nombre impair. De telles méprises dues à l’intuition sont très courantes en probabilité, et chez certains adultes, elles sont très ancrées. Le personnel enseignant doit donc recourir à plusieurs situations variées pour aider les élèves à fonder leur évaluation de la probabilité d’un événement ou d’un résultat sur la raison plutôt que sur l’intuition.
HABILETÉ À VISUALISER
« L’habileté à visualiser est un processus qui permet à l’élève de se représenter des concepts abstraits sous forme d’images mentales. Ces images lui permettent de manipuler les concepts, de les rendre signifiants et de se les approprier. » [traduction libre]
(Small, 2006, p. 132)
L’habileté à visualiser correspond à la capacité de rendre visible un phénomène ou un concept qui ne l’est pas. Les élèves peuvent ainsi :
- organiser une foule de renseignements sous la forme d’une image mentale;
- utiliser un réseau d’images mentales pour résoudre des problèmes;
- comprendre des concepts et des processus mathématiques en se référant à leur représentation visuelle.
Pour développer l’habileté à créer ces images mentales, les élèves doivent d’abord avoir eu l’occasion de voir, de créer et d’utiliser des représentations concrètes, semi-concrètes ou symboliques d’un même concept. Le personnel enseignant doit donc s’assurer de les intégrer régulièrement dans diverses situations d’apprentissage.
En traitement des données, l’habileté à visualiser est fort utile au cours du processus d’enquête; par exemple, pour bien cerner une situation donnée (étape 1), les élèves peuvent d’abord organiser leurs idées à l’aide d’une carte conceptuelle. L’image mentale qu’elles et ils se font de cette carte leur permet ensuite d’avoir en mémoire un résumé de la situation qui leur servira à toutes les étapes du processus d’enquête. Elles et ils peuvent aussi créer un diagramme, comme un diagramme à bandes ou un diagramme à ligne brisée, pour représenter des données. Elles et ils peuvent ainsi mieux en visualiser la distribution.
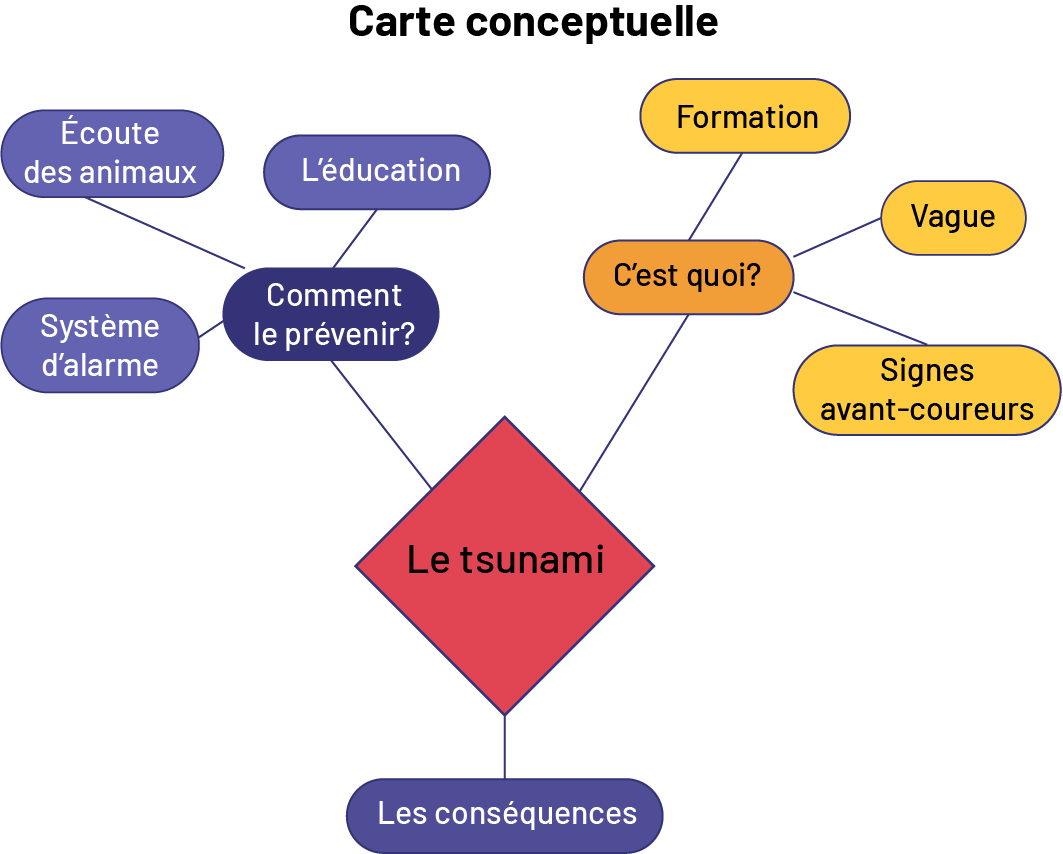 image La carte conceptuelle commence avec l’expression « Le tsunami », placée dans un carré rouge. Trois branches le relient à trois ensembles d’éléments. D’abord, elle est reliée à une bulle dans laquelle il est écrit « Comment le prévenir? ». Celle-ci se lie aux éléments suivants : « Système d’alarme. Écoute des animaux. L’éducation. » La deuxième branche se lie à une bulle dans laquelle il est écrit : « C’est quoi? ». Celle-ci se lie aux éléments suivants : « Formation. Vague. Signes avant-coureurs. » Enfin, sa troisième branche se lie à une bulle isolée, dans laquelle il est écrit : « Les conséquences ».
image La carte conceptuelle commence avec l’expression « Le tsunami », placée dans un carré rouge. Trois branches le relient à trois ensembles d’éléments. D’abord, elle est reliée à une bulle dans laquelle il est écrit « Comment le prévenir? ». Celle-ci se lie aux éléments suivants : « Système d’alarme. Écoute des animaux. L’éducation. » La deuxième branche se lie à une bulle dans laquelle il est écrit : « C’est quoi? ». Celle-ci se lie aux éléments suivants : « Formation. Vague. Signes avant-coureurs. » Enfin, sa troisième branche se lie à une bulle isolée, dans laquelle il est écrit : « Les conséquences ».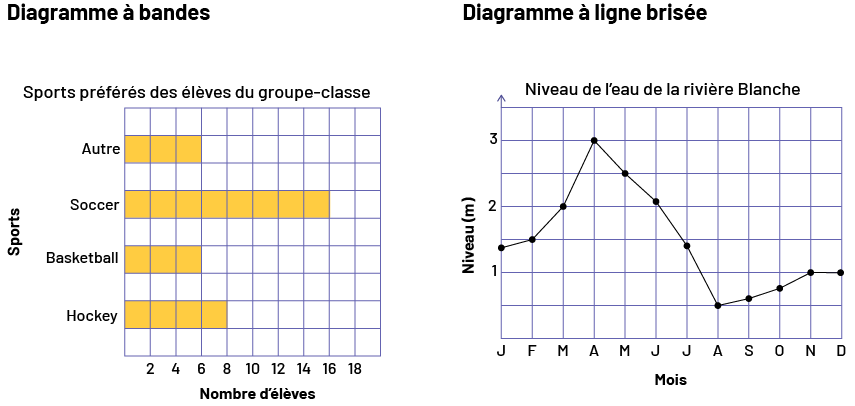 image1 Un diagramme quadrillé à bandes horizontales s’intitule « Sports préférés des filles du groupe-classe ». L’axe horizontal se nomme « Nombre d’élèves », tandis que l’axe vertical se nomme « Sports ». Pour le hockey, la bande remplit quatre cases. Pour le Basketball, la bande remplit trois cases. Pour le soccer, la bande remplit huit cases. Et pour autre, la bande remplit trois cases.image2 Le diagramme à ligne brisée à points reliés s’intitule « Niveau de l’eau de la rivière Blanche ». L’axe horizontal se nomme « Mois » tandis que l’axe vertical, gradué de zéro à trois, se nomme « Niveau en mètres ». À la lettre J, le point se situe légèrement au-dessus d’un. À la lettre F, le point se situe à un et demi. À la lettre M, le point se situe à deux. À la lettre A, le point se situe à trois. À la lettre M, le point se situe à deux et demi. À la lettre J, le point se situe au-dessus de deux. À la lettre J suivante, le point se situe entre un et un et demi. À la lettre A, le point se situe à un demi. À la lettre S, le point se situe sous le chiffre un. À la lettre O, le point se situe légèrement plus près du chiffre un. À la lettre N et à la lettre D, le point se situe à un.
image1 Un diagramme quadrillé à bandes horizontales s’intitule « Sports préférés des filles du groupe-classe ». L’axe horizontal se nomme « Nombre d’élèves », tandis que l’axe vertical se nomme « Sports ». Pour le hockey, la bande remplit quatre cases. Pour le Basketball, la bande remplit trois cases. Pour le soccer, la bande remplit huit cases. Et pour autre, la bande remplit trois cases.image2 Le diagramme à ligne brisée à points reliés s’intitule « Niveau de l’eau de la rivière Blanche ». L’axe horizontal se nomme « Mois » tandis que l’axe vertical, gradué de zéro à trois, se nomme « Niveau en mètres ». À la lettre J, le point se situe légèrement au-dessus d’un. À la lettre F, le point se situe à un et demi. À la lettre M, le point se situe à deux. À la lettre A, le point se situe à trois. À la lettre M, le point se situe à deux et demi. À la lettre J, le point se situe au-dessus de deux. À la lettre J suivante, le point se situe entre un et un et demi. À la lettre A, le point se situe à un demi. À la lettre S, le point se situe sous le chiffre un. À la lettre O, le point se situe légèrement plus près du chiffre un. À la lettre N et à la lettre D, le point se situe à un.Le modèle de partage équitable, utilisé pour déterminer une moyenne, illustre aussi la façon dont l’habileté à visualiser aide à mieux comprendre un concept abstrait. En probabilité, la ligne de probabilité constitue un moyen visuel efficace pour comprendre le concept de probabilité et comparer la probabilité de deux événements.
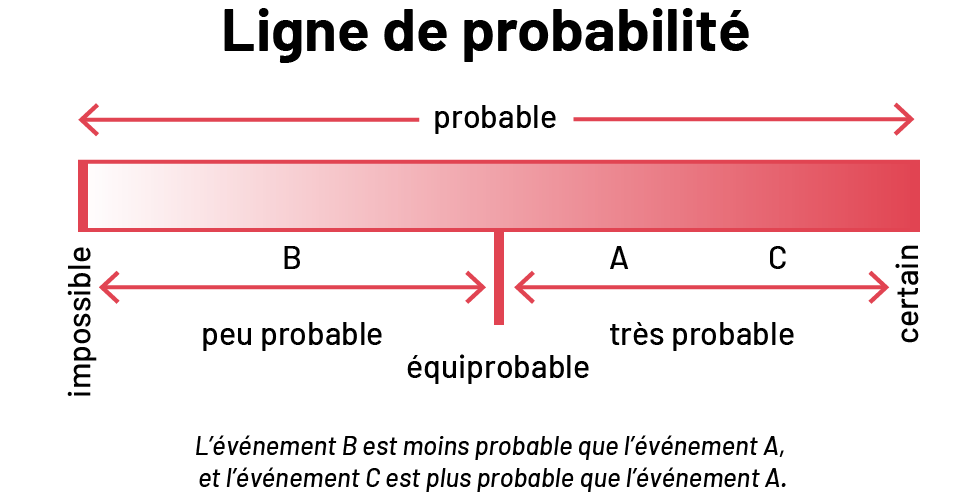 image La ligne de probabilité présente une barre partant du blanc et devenant graduellement rouge. Au-dessus de la barre, il est écrit « Probable », avec deux flèches pointant vers les extrêmes de la barre. À l’extrême gauche de la barre, il est écrit impossible. Au centre de la barre, il est écrit équiprobable. Entre la gauche et le centre, il est écrit peu probable. À l’extrême droite, il est écrit certain. Entre équiprobable et certain, il est écrit très probable. Dans la partie gauche de la barre, il y a la lettre « B ». Dans la partie droite de la barre, il y a la lettre « A » à gauche, et la lettre « C » à droite. Sous la barre, il est écrit : « L’événement B est moins probable que l’événement A, et l’événement C est plus probable que l’événement A. »
image La ligne de probabilité présente une barre partant du blanc et devenant graduellement rouge. Au-dessus de la barre, il est écrit « Probable », avec deux flèches pointant vers les extrêmes de la barre. À l’extrême gauche de la barre, il est écrit impossible. Au centre de la barre, il est écrit équiprobable. Entre la gauche et le centre, il est écrit peu probable. À l’extrême droite, il est écrit certain. Entre équiprobable et certain, il est écrit très probable. Dans la partie gauche de la barre, il y a la lettre « B ». Dans la partie droite de la barre, il y a la lettre « A » à gauche, et la lettre « C » à droite. Sous la barre, il est écrit : « L’événement B est moins probable que l’événement A, et l’événement C est plus probable que l’événement A. »De même, le diagramme en arbre constitue un moyen efficace pour visualiser l’ensemble des résultats possibles d’une expérience.
Exemple
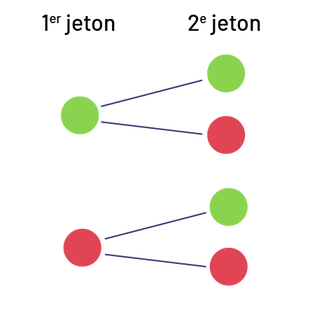
HABILETÉ À RÉSOUDRE UNE SITUATION-PROBLÈME
Dans le domaine Données, la démarche privilégiée pour résoudre une situation-problème est celle qui est habituellement associée au processus d’enquête. Comme en témoigne le tableau ci-dessous, cette démarche suit pratiquement les mêmes étapes que celles utilisées en résolution de problèmes dans les autres domaines d’étude en mathématiques. Le personnel enseignant doit aider les élèves à faire le lien entre ces étapes.
| Étapes de la résolution de problèmes | Étapes du processus d'enquête |
|---|---|
| Comprendre le problème | Cerner la situation
|
| Élaborer un plan | Faire une collecte de données
|
| Mettre le plan en œuvre | Organiser les données
|
| Vérifier les résultats | Analyser les données et interpréter les résultats
|
Comme dans les autres domaines en mathématiques, l’apprentissage des concepts du domaine Données doit se faire en situation de résolution de problèmes. Le personnel enseignant doit donc présenter aux élèves des situations engageantes qui les incitent à recourir au processus d’enquête. Il importe de souligner l’importance accrue du contexte dans ce domaine. En effet, il est pratiquement impossible de résoudre un problème sans tenir compte du contexte; par exemple, les données brutes obtenues à la suite d’une enquête menée par une tierce personne n’ont aucun sens si l’on ne sait rien au sujet de l’enquête elle-même. De même, il est impossible d’interpréter un diagramme à bandes ou un diagramme à ligne brisée si l’on ne sait pas à quoi font référence les données représentées parce que les axes sur le diagramme en question n’ont pas d’étiquettes.
Note : Pour obtenir d’autres renseignements au sujet du rôle de la résolution de problèmes en mathématiques, consulter le Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, fascicule 2 (Ministère de l’Éducation de l’Ontario, 2006, p. 1-75).
HABILETÉ À COMMUNIQUER
« La communication, sous ses multiples formes, est une fenêtre ouverte sur la pensée de l’élève; d’abord, pour comprendre ce qu’il ou elle pense, puis pour évaluer sa compréhension afin de bien orienter l’enseignement. » [traduction libre]
(Small, 2006, p. 178)
L’habileté à communiquer dans le domaine Données, ainsi que dans tous les autres domaines de mathématiques, est un moyen d’apprentissage incontournable. Elle aide, entre autres, les élèves à exprimer leur compréhension et à clarifier leur pensée. Radford et Demers (2004) soulignent que la communication sous tous ses aspects est un moyen de transformation du savoir et qu’apprendre revient à s’approprier ce savoir.
Le personnel enseignant doit favoriser un climat d’engagement au dialogue au sein du groupe-classe. Pour ce faire, il doit présenter des situations d’apprentissage d’envergure qui font en sorte que les échanges entre les élèves sont nécessaires pour comprendre le problème et trouver une solution. La communication, qu’elle soit orale ou écrite, doit faire appel aux symboles, à la terminologie et aux représentations graphiques appropriés, ainsi qu’à des raisonnements et à des arguments mathématiques qui mettent en évidence les concepts visés. Aux cycles primaire et moyen, la communication orale est un préalable à la communication écrite.
Communication orale
Les élèves doivent apprendre à utiliser la communication orale pour atteindre divers objectifs. En leur posant des questions, le personnel enseignant peut susciter des discussions qui visent un objectif en particulier. Le tableau ci-dessous en présente quelques exemples.
| Objectif | Questionnement |
|---|---|
| Relater des expériences antérieures pertinentes | Qu'avez-vous observé dans les diagrammes? Comment ont-ils été créés? Auriez-vous les mêmes résultats si vous répétiez cette expérience 10 autres fois? |
| Formuler et expliquer une prédiction | Pensez-vous qu'il y aura plus d'élèves à l'épreuve des 200 m qu'à la course à obstacles? Justifiez votre réponse. Croyez-vous qu'il est plus probable que l'aiguille s'arrête dans le secteur rouge de la roulette que dans le secteur bleu? Pourquoi? |
| Comparer différentes stratégies ou idées | Parmi la liste de questions, choisissez-en une pour effectuer votre sondage. Justifiez votre choix. Pour réaliser cette expérience de probabilité, est-il plus approprié d'utiliser une roulette ou un dé? |
| Partager une tâche | Quel est le rôle de chacun des membres de votre équipe? |
| Discuter des relations, des ressemblances ou des différences | Quelles sont les ressemblances et les différences entre ces deux tableaux? Quel rapport y a-t-il entre la fréquence de ce résultat et la fréquence de chacun des deux autres résultats? |
| Justifier | Pourquoi avez-vous choisi cette légende? Pourquoi dites-vous qu'il y a probablement plus de billes bleues que de billes rouges ou de billes jaunes dans le sac? |
| Expliquer | Quelle démarche avez-vous suivie pour recueillir vos données et les enregistrer? Quelles modifications devrait-on apporter à ce diagramme? |
Communication écrite
Consigner ses idées par écrit est habituellement plus difficile que de les exprimer oralement. Par contre, il y a des situations où le contraire est vrai; par exemple, les élèves peuvent représenter un ensemble de données statistiques de façon beaucoup plus succincte et efficace à l’aide d’un diagramme à bandes plutôt qu’à l’aide d’une description orale. Elles et ils doivent cependant apprendre à utiliser correctement les diverses représentations usuelles des données, comme un tableau de fréquences, un diagramme à bandes doubles ou un diagramme en arbre, afin de s’assurer que le message transmis sera le bon et qu’il sera bien compris par les autres. Elles et ils peuvent ensuite utiliser ces représentations pour justifier un raisonnement ou appuyer un argument au cours d’un échange mathématique en groupe-classe.
Dans le domaine Données, les élèves ont de multiples occasions d’utiliser la communication écrite. Elles et ils peuvent, par exemple :
- organiser des idées à l’aide d’une carte conceptuelle;
- formuler une question d’intérêt;
- formuler des questions de sondage;
- noter une prédiction, une observation ou une réflexion;
- compiler des données dans un tableau;
- présenter un ensemble de données dans un diagramme;
- exprimer une conclusion ou une décision;
- décrire la probabilité d’un événement.
Note : Pour obtenir d’autres renseignements au sujet du rôle de la communication orale et de la communication écrite en mathématiques, consulter le Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, fascicule 2 (Ministère de l’Éducation de l’Ontario, 2006, p. 77-114).
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 12-19.
« Les élèves ne peuvent pas nécessairement améliorer par eux-mêmes la formulation de leurs questions, identifier différentes méthodes de collecte de données ou choisir la façon la plus appropriée pour organiser et représenter des données; ces habiletés s’acquièrent grâce à la pratique, aux échanges mathématiques et aux interventions du personnel enseignant. » [traduction libre]
(National Council of Teachers of Mathematics, 2000, p. 110)
Les élèves ont besoin d’être guidées et guidés ainsi que d’encadrement pour apprendre à résoudre des problèmes liés aux données et à la probabilité. Le personnel enseignant doit avoir une vue d’ensemble du parcours que doivent suivre les élèves et planifier les activités d’apprentissage en conséquence. Il doit trouver les situations où il est important de recourir à l’enseignement explicite en s’assurant de modeler sa démarche, ses interrogations et son raisonnement. De plus, le personnel enseignant doit :
- proposer aux élèves une variété de situations d’apprentissage engageantes et à un degré de difficulté approprié;
- encourager les élèves à utiliser du matériel concret et semi-concret;
- s’assurer que les élèves utilisent de façon appropriée la terminologie relative au traitement des données et à la probabilité;
- mettre l’accent sur la compréhension des concepts;
- poser des questions qui aident les élèves à franchir une certaine étape ou qui les incitent à réfléchir et à clarifier leur pensée.
Un enseignement efficace dans le domaine Données implique aussi le développement simultané chez les élèves de la pensée probabiliste et des compétences en matière de littératie statistique. Il importe donc d’aider les élèves à établir des liens entre les concepts relatifs au traitement des données et ceux relatifs à la probabilité. Pour ce faire, le personnel enseignant doit choisir des situations d’apprentissage qui les aideront à établir ces liens; par exemple, le personnel enseignant leur demande de déterminer la probabilité d’un événement en partant de données issues d’une enquête (exemple 1) ou de suivre certaines des étapes du processus d’enquête en partant de données issues d’une expérience de probabilité (exemple 2).
Exemple 1
Chaque élève du groupe-classe révèle le mois de son anniversaire de naissance. Elle ou il crée ensuite un diagramme à bandes qui représente ces données. Le personnel enseignant met les noms dans un sac et demande aux élèves d’utiliser ce diagramme pour déterminer la probabilité de tirer le nom d’une ou d’un élève dont l’anniversaire est en novembre. (La probabilité est de 3/25.)
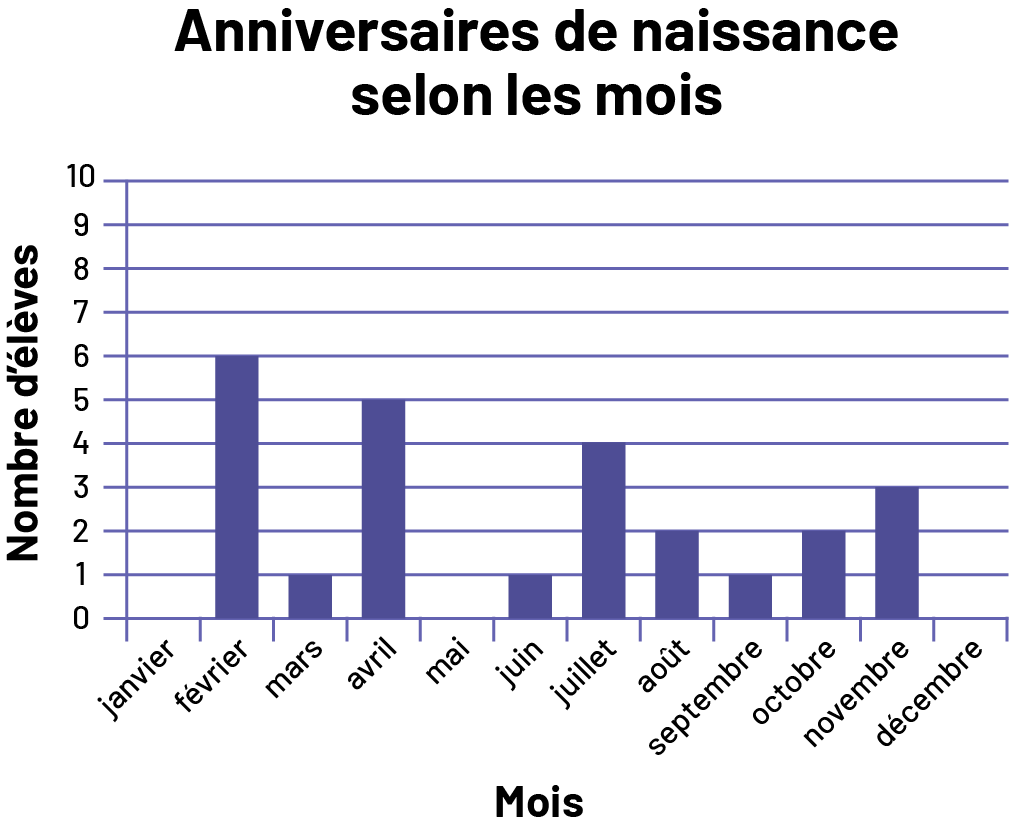 image Le diagramme à bandes s’intitule « Anniversaires de naissance selon les mois ». L’axe vertical correspond aux mois tandis que l’axe vertical, gradué de zéro à dix, correspond au nombre d’élèves. Il n’y a aucune bande en janvier. En février, la bande s’élève à six. En mars, la bande s’élève à un. En avril, la bande s’élève à cinq. En mai, il n’y a aucune bande. En juin, la bande s’élève à un. En juillet, la bande s’élève à quatre. En août, la bande s’élève à deux. En septembre, la bande s’élève à un. En octobre, la bande s’élève à deux. En novembre, la bande s’élève à trois. Et en décembre, il n’y a aucune bande.
image Le diagramme à bandes s’intitule « Anniversaires de naissance selon les mois ». L’axe vertical correspond aux mois tandis que l’axe vertical, gradué de zéro à dix, correspond au nombre d’élèves. Il n’y a aucune bande en janvier. En février, la bande s’élève à six. En mars, la bande s’élève à un. En avril, la bande s’élève à cinq. En mai, il n’y a aucune bande. En juin, la bande s’élève à un. En juillet, la bande s’élève à quatre. En août, la bande s’élève à deux. En septembre, la bande s’élève à un. En octobre, la bande s’élève à deux. En novembre, la bande s’élève à trois. Et en décembre, il n’y a aucune bande. Exemple 2
Le personnel enseignant remet à chaque équipe de deux un sac contenant 50 jetons, dont certains sont rouges et d’autres, bleus. Il leur propose de mener une expérience de probabilité afin de déterminer le nombre probable de jetons de chaque couleur. Chaque équipe doit tirer 100 fois un jeton du sac, noter sa couleur et remettre le jeton dans le sac. Pour compiler les données, les élèves doivent utiliser un tableau de fréquences.
À titre d’exemple, une équipe a construit le tableau suivant.
 image Le tableau de fréquences possède trois colonnes : Couleur, dénombrement et fréquence. Pour la couleur rouge, on dénombre 5 ensembles de 5 traits et deux traits seuls. Il est écrit 37 sous Fréquence. Pour la couleur bleue, on dénombre 12 ensembles de 5 traits et 3 traits seuls. Il est écrit 63 sous Fréquence.
image Le tableau de fréquences possède trois colonnes : Couleur, dénombrement et fréquence. Pour la couleur rouge, on dénombre 5 ensembles de 5 traits et deux traits seuls. Il est écrit 37 sous Fréquence. Pour la couleur bleue, on dénombre 12 ensembles de 5 traits et 3 traits seuls. Il est écrit 63 sous Fréquence.D’après les données représentées dans ce tableau, les élèves pourraient conclure que, dans leur sac, il y a environ 20 jetons rouges et 30 jetons bleus.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 20-21.
ÉCHANGE MATHÉMATIQUE
L’échange mathématique est un temps d’objectivation, pendant ou après l’apprentissage, qui va au-delà du simple échange d’idées et de stratégies qu’utilisent les élèves. Au cours de l’échange, les élèves cherchent à défendre leurs idées et à convaincre les autres du bien-fondé de leurs stratégies et de leurs solutions.
L’échange mathématique est un moment pédagogique fort au cours duquel le personnel enseignant dirige les discussions de façon stratégique afin de faire ressortir des idées mathématiques importantes. Celui-ci se prête bien à une approche pédagogique fondée sur la vision que les élèves forment une communauté d’apprentissage.
Points à considérer
- Afin de faciliter la discussion pendant l’échange mathématique, organiser une aire de rencontre. Les élèves pourront y échanger des idées et présenter des exposés en renforçant leur sentiment d’appartenance à la communauté. L’aire de rencontre doit :
- être spacieuse et bien définie pour que les élèves puissent s’y rassembler pour échanger, discuter et faire des présentations;
- être assez grande pour que chaque élève puisse bouger ou remuer un peu sans déranger les autres;
- être éloignée des étagères de rangement, qui pourraient être une source de distraction pendant la rencontre;
- être près des référentiels pour s’y référer, au besoin;
- être près des outils de présentation.
- Au cours de l’exploration, le personnel enseignant circule parmi les élèves, observe la démarche des équipes et écoute leurs discussions. Ses observations lui permettent de choisir l’ordre des présentations en vue de l’échange. Ce choix est guidé par l’objectif qu’il s’est fixé, comme l’application d’une stratégie et l’utilisation d’un modèle mathématique, pour assurer la compréhension des concepts.
- La présentation du travail de chaque élève n’est pas nécessaire; il est préférable de se limiter à présenter les démarches ou les solutions qui se distinguent. Demander aux élèves de montrer leur solution ou leur démarche si elle est semblable à celle présentée, sans toutefois l’expliquer. S’assurer de choisir des élèves différentes et différents d’un échange à l’autre.
- Pendant l’échange, inviter chaque membre de l’équipe à présenter sa réflexion quant au travail accompli après avoir préparé des arguments clairs et convaincants.
- Pendant l’échange, inviter les élèves à poser des questions sur la démarche et les explications de celles et de ceux qui font une présentation. Ce questionnement favorise la vérification de leur propre compréhension et fait en sorte que les présentatrices et les présentateurs ajustent, elles et eux aussi, leur compréhension.
- Créer, dans la salle de classe, un climat de confiance et de respect où toutes et tous les élèves sont encouragés à prendre part aux activités et où tous les propos sont valorisés; par exemple, une ou un élève doit se sentir à l’aise de présenter une erreur dans son travail à titre de contre-exemple qui aidera à la compréhension de toutes et de tous.
- Poser aux élèves des questions stratégiques afin de les aider à bâtir une bonne compréhension des concepts. En voici quelques exemples :
- Quelqu’un peut-il résumer l’idée présentée?
- Comment as-tu procédé pour...?
- Comment as-tu surmonté cette difficulté?
- Pourquoi as-tu employé cette stratégie?
Pour obtenir de plus amples renseignements au sujet de l’échange mathématique, consulter le Guide d’enseignement efficace des mathématiques, de la maternelle à la 6e année, fascicule 3 (Ministère de l’Éducation de l’Ontario, 2006).
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 283-284.
