F1. Argent et finances
Démontrer sa compréhension de la valeur de la monnaie canadienne.
Situation d’apprentissage : La tirelire mystérieuse
Durée totale : de 45 à 55 minutes
Sommaire
Dans cette situation d’apprentissage, l’élève apprend à regrouper et à compter des pièces de monnaie et des billets en dollar canadien, en formant différentes combinaisons dont la somme sera équivalente à un montant d’argent ciblé.
|
Attente |
Contenus d’apprentissage |
|
F1. Littératie financière Démontrer sa compréhension de la valeur de la monnaie canadienne. |
F1.1 Déterminer différentes façons d’arriver au même montant d’argent en monnaie canadienne jusqu’à 200 ¢ avec diverses combinaisons de pièces de monnaie, et jusqu’à 200 $ avec différentes combinaisons de pièces de 1 $ et de 2 $ et de billets de 5 $, 10 $, 20 $, 50 $ et 100 $. |
| Pratiques pédagogiques à fort impact en mathématiques à privilégier | Description |
|---|---|
|
Résultats d’apprentissage, critères d’évaluation et rétroaction descriptive |
Avant de commencer cette situation d’apprentissage, il est essentiel de rendre explicite le résultat d’apprentissage, déterminé à partir des attentes et des contenus du programme-cadre, afin qu’il soit bien connu et compris de l'ensemble des élèves. Ainsi, elles et ils prennent conscience des objectifs d’apprentissage de la leçon. Les critères d’évaluation peuvent ensuite être élaborés et bien compris grâce à différentes stratégies pédagogiques, telles que des exemples de travaux d’élèves, la coconstruction des critères d’évaluation ou encore une autoévaluation de la compréhension des critères. Ces stratégies permettent un engagement de la part des élèves et une compréhension commune des étapes nécessaires pour atteindre l’objectif ciblé. Il est important de rendre le résultat d’apprentissage et les critères d’évaluation visibles en les affichant dans la salle de classe pour que les élèves s’y réfèrent tout au long de la leçon. La rétroaction descriptive en lien avec les critères ciblés donne les renseignements précis dont les élèves ont besoin pour atteindre le résultat d’apprentissage visé. En donnant, à de multiples occasions, de la rétroaction descriptive, les élèves acquièrent des habiletés pour évaluer leur propre apprentissage au fur et à mesure qu’elles et ils réfléchissent aux critères d’évaluation. Dans cette situation d’apprentissage, un moment propice pour la rétroaction descriptive est lors du déroulement. Les élèves représentent, à l'aide de modèles, différentes combinaisons d'une somme d'argent donnée. Les élèves travaillent et communiquent en petits groupes, et, à l’aide de questions judicieuses, le personnel enseignant vérifie la compréhension des élèves et les dirige vers les critères d’évaluation ciblés pour qu’elles et ils ajustent leur travail ou justification. Lors de l’objectivation, les échanges mathématiques peuvent nécessiter la rétroaction descriptive du personnel enseignant pour s’assurer que l’élève possède les outils nécessaires pour faire un réinvestissement de ses habiletés et ses connaissances dans un autre contexte. |
|
Tâches et expériences de résolution de problèmes |
Cette situation d’apprentissage, où l’élève doit faire plusieurs combinaisons de monnaie canadienne, est une expérience de résolution de problèmes, puisqu’elle donne l’occasion à l’élève de raisonner, de communiquer, de représenter, de faire des liens ainsi que de justifier sa pensée. Cette situation d’apprentissage comporte plusieurs points d’entrée puisque peu importe le degré de préparation, chaque élève pourra participer et proposer des solutions en utilisant ses stratégies, ainsi que sa pensée critique et créative. Cela favorise l’accessibilité pour l'ensemble des élèves ainsi que l’échange d’une variété de stratégies et d’idées mathématiques. Le déroulement de cette situation d’apprentissage peut être différencié avec l’utilisation de nombres différents pour les équipes de travail (nombres plus petits, donc exercice moins complexe ou nombres plus grands pour un exercice plus complexe), cela rend la tâche accessible tout en représentant un défi pour les élèves. |
|
Conversations mathématiques |
En planifiant des situations d’apprentissage comme celle-ci, qui mettent l’accent sur la collaboration et le travail d’équipe, les conversations mathématiques sont continuelles. Celles-ci permettent aux élèves de s’exprimer et de réagir aux idées mathématiques présentées. Le rôle du personnel enseignant se définira par l’habileté à poser des questions ouvertes provoquant des réflexions chez les élèves pour stimuler leur pensée et permettant des réponses multiples. Cette interaction par le questionnement doit être planifiée minutieusement pour mettre en évidence les concepts clés, les habiletés ou des représentations spécifiques pour favoriser la progression des élèves. Le personnel enseignant est encouragé à anticiper les questions et les réponses d’élèves afin de rendre l’exercice encore plus stratégique (par exemple, en anticipant certaines erreurs communes). Dès la mise en situation, des pistes de questionnement accessibles à toutes et à tous encouragent les élèves à échanger leurs idées en groupe-classe. Lors du déroulement, le questionnement envers le travail ou la discussion des élèves favorise leur justification en équipe et développe leur pensée critique. Lors de l’objectivation, les pistes de questionnement aideront la conversation mathématique en groupe-classe et donneront au personnel enseignant une idée de la compréhension des élèves. |
|
Regroupements flexibles |
Les regroupements flexibles peuvent favoriser la collaboration et donner aux élèves l’occasion de participer à de riches conversations mathématiques, d’apprendre les uns des autres et de faire évoluer leur réflexion mathématique. Cela permet aux élèves de travailler indépendamment du personnel enseignant, tout en bénéficiant de l’appui de leurs pairs. C’est la combinaison intentionnelle d’expériences de travail en grands groupes, en petits groupes, en équipes de deux et individuelles qui peut favoriser un milieu d’apprentissage mathématique riche. Pour cette situation d’apprentissage, la mise en situation peut être faite en groupe-classe. Lors du déroulement, de petits groupes de deux ou trois sont préférables pour favoriser la participation de chaque élève lors de l’équivalence monétaire. L’objectivation en groupe-classe permet aux élèves d’entendre les idées des autres, tout en apportant leurs idées à la discussion. Le choix de regroupements flexibles peut être adapté selon les besoins de votre groupe-classe. |
Connaissances et habiletés en développement
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent pouvoir :
- Compter jusqu’à 200 par intervalles de 1, de 2, de 5, de 10, de 25 et de 100.
- Lire, représenter, composer et décomposer les nombres naturels de 0 à 200.
- Utiliser les propriétés de l’addition et se rappeler des faits d’addition de nombres jusqu’à 20.
- Utiliser des égalités pour représenter, décrire et résoudre des situations relatives à l’addition de nombres naturels dont la somme est égale ou inférieure à 100.
Résultat d’apprentissage
À la fin de cette situation d’apprentissage, l’élève pourra trouver différentes combinaisons de pièces de monnaie et de billets de dollars canadiens pour représenter un montant d’argent de différentes façons.
Critères d’évaluation possibles selon les grilles d’évaluation du rendement
| Compétence | Critère(s) d’évaluation |
|---|---|
|
Connaissance et compréhension |
L’élève comprend en quoi consistent les relations d’équivalence entre deux combinaisons de pièces ou de billets qui représentent le même montant d’argent. |
|
Habiletés de la pensée |
L’élève choisit des stratégies pour additionner les pièces de monnaie et les billets. |
|
Communication |
L'élève communique son raisonnement mathématique à l'aide de symboles, de dessins, d'explications et de matériel de manipulation. |
|
Mise en application |
L’élève compte par intervalles de 5, de 10 et de 25 pour regrouper les pièces et les billets de monnaie canadienne. L’élève applique les stratégies pour additionner les pièces de monnaie et les billets afin de représenter une variété de combinaisons possibles, et ce, pour différents montants d’argent. |
Matériel nécessaire
- ensemble de pièces de monnaie et de billets de dollar canadien factices;
- tableau blanc effaçable, papier grand format ou autre surface pour permettre aux élèves de noter leurs combinaisons;
- appui visuel pour afficher la résolution de problème (par exemple, tableau blanc interactif, cartes-éclairs, bandes de papier);
- annexe 1 (Droite ouverte);
- annexe 2 (Modèle vierge);
- annexe 3 (Modèles de pièces de 5 ¢, de 10 ¢ et de 25 ¢);
- annexe 4 (Modèles de billets jusqu’à 50 $ et de pièces de 1 $ et plus);
- annexe (Pièces de la tirelire de Sofia)
Vocabulaire mathématique
acheter, additionner, addition répétée, billets, combinaison, composer, compter par intervalles, décomposer, dollar canadien, économiser, équivalence, nombres repères, pièces de monnaie, quantité, représenter, somme, total, valeur
Mise en situation
Durée : 20 minutes
L’évaluation peut se faire par les…
Présenter la situation suivante aux élèves :
Sofia a économisé assez d’argent pour s’acheter une surprise au magasin Le roi du dollar. Lorsqu’elle fouille dans sa tirelire, elle trouve différentes pièces de monnaie, mais pas de pièce de 2 $. Quelle combinaison de pièces de monnaie peut-elle faire pour obtenir la somme de 2 $?
Demander aux élèves d’observer les pièces qui se trouvent dans la tirelire de Sofia.
Voici les pièces de monnaie dans la tirelire de Sofia :

À l’aide des annexes 1 et 2, demander aux élèves de représenter la valeur des pièces ci-dessus. Cela permet aux élèves d’avoir une représentation concrète de la valeur des pièces.
Poser des questions aux élèves afin de stimuler leur réflexion et les encourager à échanger leurs idées entre elles et eux. Voici des pistes de questionnement possibles :
- En regardant le contenu de la tirelire de Sofia et les modèles, que remarques-tu?
- Qu’est-ce qui se ressemble? Qu’est-ce qui est différent?
- En observant les pièces de monnaie, comment pourrais-tu les regrouper pour les compter? Est-ce que tu connais plus d’une façon de les compter?
- En observant les modèles des pièces de monnaie, comment pourrais-tu les regrouper pour les compter? Est-ce que tu connais plus d’une façon de les compter?
- En observant les modèles, tu vois que 1 $ = 100 ¢ et que 2 $ = 200 ¢. Est-ce possible d’obtenir la somme de 2 $ avec les pièces de monnaie de 5 ¢, 10 ¢, 25 ¢ et la pièce de 1 $? Comment le sais-tu?
- Combien de combinaisons différentes pouvons-nous faire pour obtenir un montant total de 2 $?
- En faisant des combinaisons différentes, comment peut-on varier les pièces (ou les modèles) pour représenter le même montant (par exemple, de quelles façons peut-on échanger une pièce de 25 ¢)?
- Si nous avons des combinaisons comprenant plusieurs pièces de monnaie, est-ce que cela change la valeur totale? Comment le sais-tu?
- Comment pouvons-nous obtenir la somme de 2 $ en combinant le moins de pièces possible? le moins de modèles possible?
- Comment pouvons-nous obtenir la somme de 2 $ en combinant le plus de pièces possible? le plus de modèles possible?
Déroulement
Durée : 25 minutes
L’évaluation peut se faire par les…
Expliquer aux élèves que chaque équipe recevra le contenu d’une tirelire qui n’est pas celle de Sofia. Les pièces de monnaie et de dollars retrouvés dans cette tirelire sera donc un mystère! Pour s’acheter une surprise au magasin Le roi du dollar, les équipes devront représenter un montant qui leur sera assigné par le personnel enseignant (par exemple, 5 $, 12 $, 37 $, 74 $, 65 ¢, 95 ¢).
Former des équipes de deux ou de trois élèves.
Distribuer une quantité d’argent factice aux élèves dans un petit sac pour représenter le contenu d’une des tirelires mystères.
Distribuer une trousse de modèles annexes 1 à 4 aux élèves afin de leur permettre de visualiser la valeur des billets et des pièces.
S’assurer de varier les pièces de monnaie et les billets dans le petit sac à remettre à chaque équipe pour favoriser leur questionnement lors de la résolution de problème.
Inviter les élèves à discuter et à trouver le plus de combinaisons possibles qui équivalent au montant d’argent assigné.
Demander aux élèves de noter leurs différentes combinaisons.
Circuler, observer et poser des questions aux élèves.
Par exemple :
- Quelles pièces de monnaie et quels billets avez-vous regroupés?
- Pourquoi avez-vous choisi de les regrouper de cette façon?
- Comment les avez-vous comptés?
- De quelle autre façon est-ce possible de représenter ce montant?
- Est-ce nécessaire d’utiliser toutes les pièces et tous les billets?
|
Observations possibles |
Interventions possibles |
|
Des élèves ont de la difficulté à compter par intervalles (par exemple, 5 et 25). |
|
|
L’équipe représente la somme d’argent en utilisant les mêmes pièces de monnaie sans les faire varier dans les différentes combinaisons (par exemple, 10 pièces de 10 ¢, 4 pièces de 25 ¢). |
|
|
L’équipe éprouve de la difficulté à additionner les pièces de monnaie ou les billets qui font partie de la combinaison choisie. |
|
Réponse possible
Une équipe reçoit un sac mystère contenant :
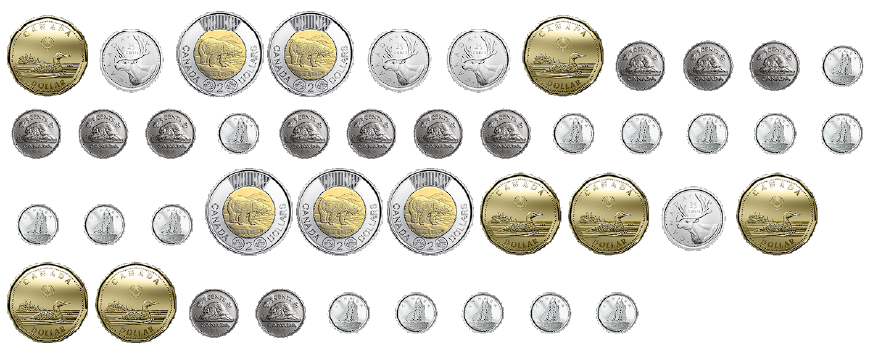
L’équipe doit représenter le montant de 12 $ avec les pièces de monnaie de son sac mystère. L’équipe peut utiliser les modèles pour représenter les pièces.
En discutant, en estimant, en calculant et en utilisant le matériel de manipulation, voici les diverses combinaisons que l’équipe a trouvées :
5 pièces de 2 $ et 2 pièces de 1 $ = 12 $
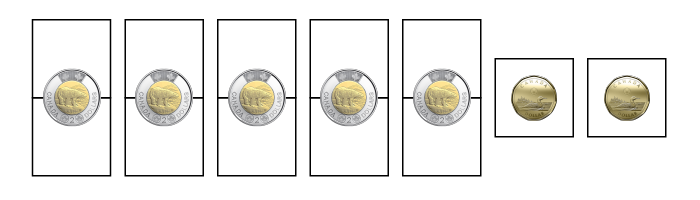
4 pièces de 2 $ et 4 pièces de 1 $ = 12 $
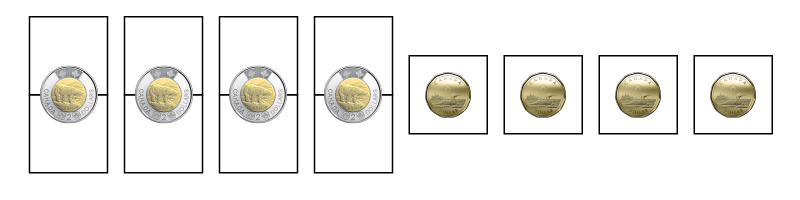
3 pièces de 2 $ et 6 pièces de 1 $ = 12 $
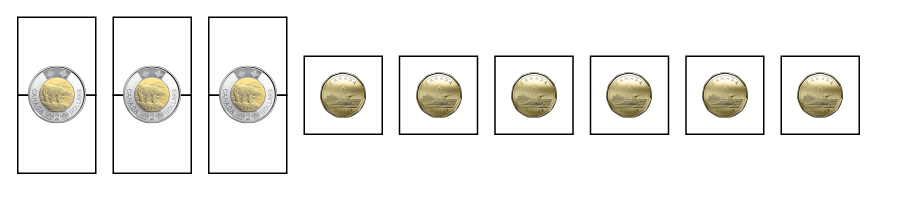
2 pièces de 2 $, 6 pièces de 1 $, 4 pièces de 25 ¢, 10 pièces de 10 ¢ = 12 $
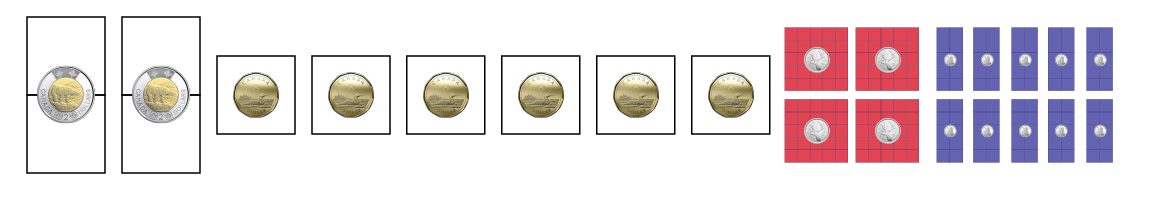
2 pièces de 2 $, 7 pièces de 1 $, 4 pièces de 25 ¢ = 12 $
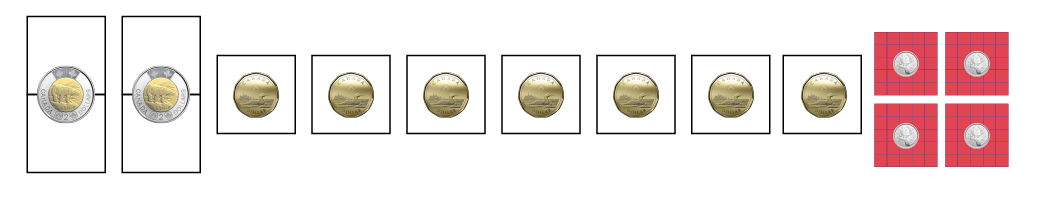
2 pièces de 2 $, 7 pièces de 1 $, 10 pièces de 10 ¢ = 12 $
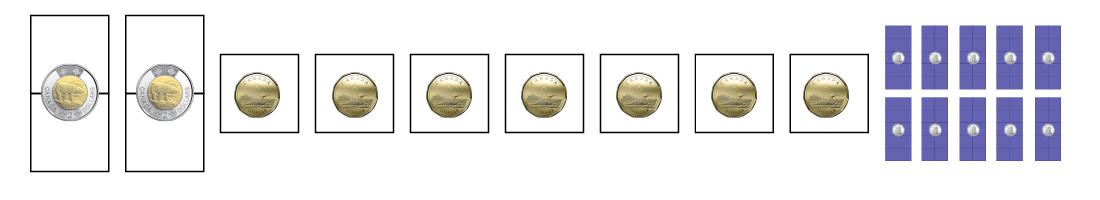
1 pièce de 2 $, 7 pièces de 1 $, 4 pièces de 25 ¢, 15 pièces de 10 ¢ et 10 pièces de 5 ¢ = 12 $.

Note : Amener les élèves à remarquer les régularités dans l’échange de pièces pour créer différentes combinaisons (par exemple, pour remplacer une pièce de 2 $, il me faut 2 pièces de 1 $). Ces relations ont un lien avec le contenu C1.4 du domaine Algèbre.
Objectivation
Durée : 10 minutes
L’évaluation peut se faire par les…
Lorsque les élèves auront épuisé les possibilités, leur demander de circuler pour observer les montants et les combinaisons des autres équipes afin de comparer les représentations.
Poser des questions aux élèves dans le but d’approfondir leur réflexion :
- Selon toi, pourquoi est-ce important de pouvoir faire plusieurs combinaisons pour représenter un montant d’argent?
- Selon toi, lorsqu’on fait l’achat d’un bien ou d’un service, est-ce qu’il est préférable d’utiliser le plus de pièces possible ou le moins de pièces possible?
- En regardant les diverses représentations des autres équipes, quelles sont les ressemblances et les différences?
- Quelle stratégie aimerais-tu utiliser la prochaine fois? Explique pourquoi.
- Quelle représentation ou stratégie te semble la plus efficace? Explique pourquoi.
- En faisant une réflexion personnelle, est-ce que tu penses avoir atteint le résultat d’apprentissage?
- Comment te sentais-tu lors du travail en équipe? Quelles émotions as-tu ressenties? Lors des prochains travaux d’équipe, quelles stratégies pourrais-tu mettre en place pour vivre une expérience plus positive?
Faire un retour avec les élèves afin de leur expliquer que la valeur totale reste toujours la même, peu importe le nombre de pièces qui sont combinées. L’important est de reconnaître la valeur des pièces de monnaie et de voir comment on peut les regrouper pour obtenir le même montant. L’utilisation des modèles permet à l’élève de visualiser les valeurs des pièces et donc le montant d’argent à représenter.
Consolidation
- Demander à chaque groupe d’élèves de remplir un petit sac représentant une tirelire et de choisir un montant pour qu’un autre groupe puisse le représenter avec de l’argent factice. Demander aux groupes de faire quelques combinaisons d’abord afin de s’assurer que les pièces mises dans la tirelire soient suffisantes et variées pour le montant donné.
- Montrer de la nourriture ou des objets que les élèves connaissent au tableau interactif, par exemple des fruits, des collations, des jeux éducatifs ou autres. Demander aux groupes d’élèves tout d’abord de deviner le prix de l’objet, puis de demander aux élèves de choisir les pièces et les billets d’argent factice nécessaires pour le payer. Montrer le prix de la nourriture ou de l’objet. Demander aux groupes de faire plus d’une combinaison pour arriver au prix. Demander aux élèves de se promener dans la classe pour voir les différentes combinaisons possibles pour le même montant.
Liens avec les autres domaines mathématiques
Nombres
B1.1 Lire, représenter, composer et décomposer les nombres naturels de 0 jusqu’à 200, à l’aide d’une variété d’outils et de stratégies, dans divers contextes, et décrire de quelles façons ils sont utilisés dans la vie quotidienne.
B1.4 Compter jusqu’à 200, y compris par intervalles de 20, 25 et 50, à l’aide d’une variété d’outils et de stratégies.
B2.2 Se rappeler les faits d’addition et de soustraction de nombres jusqu’à 20 et les faits de la soustraction associés, et démontrer sa compréhension de ces faits.
B2.4 Utiliser des objets, des schémas et des équations pour représenter, décrire et résoudre des situations relatives à l’addition de nombres naturels dont la somme est égale ou inférieure à 100 et à la soustraction de nombres égaux ou inférieurs à 100.
Algèbre
C1.4 Créer et décrire des suites comprenant des nombres naturels jusqu’à 100, et représenter des relations entre ces nombres.
C2.3 Déterminer et utiliser des relations d’équivalence comprenant des nombres naturels jusqu’à 100, dans divers contextes.
Différenciation pédagogique et conception universelle de l’apprentissage
- Fournir un appui visuel (référentiel) aux élèves pour identifier avec plus de facilité les pièces de monnaie et leur valeur.
- Modéliser la tâche avec un petit groupe en représentant les équivalences monétaires.
- Mettre à la disposition de l’élève une grille de 100, un Rekenrek ou tout autre matériel de manipulation lui permettant de dénombrer plus facilement.
- Selon les champs d’intérêt des élèves, adapter la situation d’apprentissage, changer le nom du magasin et les achats à faire.
- Dans un premier temps, n’offrir que des pièces de 5 ¢ et de 10 ¢ à certaines équipes ou des pièces de 1 $, des billets de 5 $ et de 10 $ pour faciliter la tâche de compter par intervalles, en offrant la référence aux points d’ancrage de 5 et de 10.
Pour un défi supplémentaire
- N’offrir que certaines pièces de monnaie ou que certains billets pour représenter les différents montants d’argent (développer l’habileté de la pensée chez les élèves).
- Encourager le calcul mental chez les élèves et les inviter à valider leurs réponses à l’aide du matériel concret.
- Inciter les élèves à explorer et à utiliser du matériel de manipulation divers pour représenter un même montant d’argent.
Source : Guide d’enseignement efficace des mathématiques, Littératie financière, p. 99-107.
