B1.7 Reconnaître l’équivalence entre un tiers et deux sixièmes d’un même tout, dans des contextes de partage équitable d’une quantité.
Activité 1 : quelle partie? (représenter les fractions équivalentes)
Démarche
Remettre 12 jetons bicolores à chaque élève ou à chaque équipe de deux.
Demander aux élèves de diviser les jetons en quatre groupes égaux de la même couleur.
Poser aux élèves les questions suivantes :
- Si je divise les jetons en quatre groupes égaux, comment appelle-t-on ces groupes?
- Que représente chacun de ces groupes égaux?
- Comment écrirais-tu la fraction pour représenter chacun de ces groupes?
Demander aux élèves de diviser les jetons en quatre groupes égaux : deux groupes d’une couleur et deux groupes d’une autre couleur.
Poser aux élèves les questions suivantes :
- Si je divise les jetons en quatre groupes égaux, que représente chacun de ces groupes?
- Quelle fraction de l’ensemble représente un groupe de trois jetons?
- Comment écrirais-tu la fraction pour représenter ce groupe?
- Quelle fraction de l’ensemble chaque groupe rouge représente-t-il?
- Quelle fraction de l’ensemble les deux groupes rouges représentent-ils?
- Comment écrirais-tu la fraction pour représenter ces deux groupes?
Note : Pour identifier les différents groupes, écrire le nom de la fraction en lettres (par exemple, un quart). Il est important que les élèves associent le nom de la fraction (par exemple, un quart) au nombre de groupes ou de parties avant de les exposer à sa forme écrite en chiffres (par exemple, \(\frac{1}{4}\)).
Reprendre l’activité, cette fois-ci avec les tiers et les sixièmes.
Intervention
Au moment de l’objectivation, poser aux élèves des questions telles que :
- Que représente le nombre au-dessus de la barre de fraction?
- Que représente le nombre sous la barre de fraction?
- En combien de parties égales l’ensemble est-il divisé, si une partie se nomme un tiers? un quart? un sixième?
Inspiré de Marilyn Burns, « Fractions with Two Color Counters », About Teaching Mathematics, p. 225-226.
Source : Guide d'enseignement efficace des mathématiques de la 1re à la 3e année, p. 54.
Activité 2 : comparaison de fractions
Présenter aux élèves la situation suivante.
Arturri et Sophie jouent à un jeu vidéo. Pour gagner, ils doivent franchir 12 niveaux. Les 12 niveaux représentent le tout. Arturri a réussi un tiers des niveaux. Sophie en a réussi deux sixièmes. À présent, qui a réussi le plus de niveaux?
Représentation de fractions équivalentes à l’aide d’un modèle de longueur
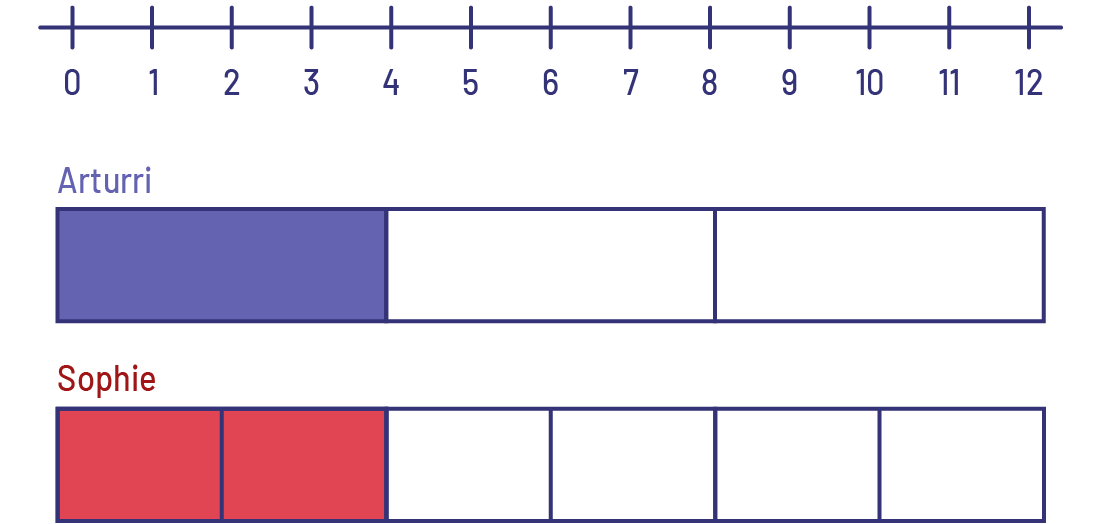
La droite numérique est numérotée de zéro à douze. En dessous, il y a une barre associée au nom Arturri. Elle est divisée en trois parties égales, donc va de zéro à quatre, de quatre à huit et de huit à douze. La première partie est colorée en violet. En dessous, il y a une barre associée au nom Sophie. Elle est divisée en six parties égales, donc suit les bonds de deux. Les deux premières parties sont colorées en rouge et équivalent à la partie violette d’Arturri.
Je dessine 1 un tiers du tout sur une bande fractionnaire pour représenter les niveaux qu’a réussis Arturri.
Je dessine 2 un sixième du tout sur une bande fractionnaire pour représenter les niveaux qu’a réussis Sophie.
En observant les deux bandes fractionnaires, je comprends qu’Arturri et Sophie ont réussi le même nombre de niveaux. Alors, un tiers et 2 un sixième (deux sixièmes) sont des fractions équivalentes.
Source : En avant les maths!, 2e année, CM, Nombres, p. 3.
