À vue d'oeil...

Habileté : se rappeler des faits d’addition de nombres jusqu’à 20 et des faits de soustraction associés

---

Il existe de nombreuses stratégies pouvant aider les élèves à développer leur sens des opérations arithmétiques. Les élèves n’utilisent pas tous l’éventail complet des stratégies; certaines et certains en utilisent une, par exemple, la stratégie des doubles. Les élèves abandonnent les stratégies dont elles et ils n’ont plus besoin au fur et à mesure qu’elles et ils en découvrent et en créent d’autres encore plus efficaces.

Aux cycles préparatoire et primaire, les élèves utilisent d’abord des objets ou leurs doigts pour se représenter les problèmes. Puis, tirant avantage de ces expériences, elles et ils commencent à utiliser des stratégies de dénombrement plus avancées.

Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6^e année, p. 11 et 12.

Représentation des faits numériques de base

Utiliser des modèles pour représenter les faits numériques de base peut aider les élèves à comprendre le sens des opérations fondamentales et à en amoindrir le caractère abstrait. De nombreux modèles peuvent être élaborés à l’aide du matériel ci-dessous pour amener les élèves à comprendre l’addition et la soustraction :

• des objets, comme les jetons ou les carreaux;
• du matériel visuel, comme des illustrations;
• le cadre à cinq cases;
• le cadre à dix cases;
• les tapis de réunion;
• les carreaux de deux couleurs;
• la droite numérique;
• les grilles de nombres.

Les modèles aident les élèves à établir des relations et ainsi à mieux comprendre ce que les symboles représentent dans les opérations. Ainsi, les élèves peuvent utiliser un algorithme d’addition ou de soustraction, selon leur façon de se représenter le problème. Il est possible d’aider les élèves à comprendre le problème d’abord avec du matériel de manipulation, puis avec des symboles comme les signes =, + et –.

Les modèles aident les élèves à établir des liens entre les dessins ou les illustrations, les symboles et les mots. On trouvera ci-dessous différents modèles pouvant représenter pour des élèves le fait de base 6 + 3. Chacune des quatre représentations est appropriée. Cependant, les élèves éprouveront moins souvent le besoin de recourir aux représentations visuelles à mesure qu’elles et ils développeront certains automatismes pour résoudre les faits numériques de base.

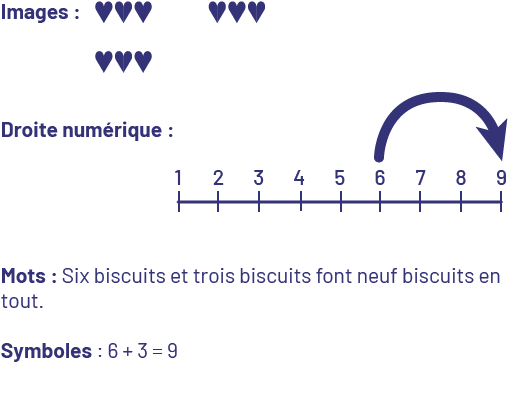
À côté du mot « Images », il y a trois ensembles de trois cœurs. À côté de l’expression « Droite numérique », il y a une droite numérotée d’un à neuf. Une flèche courbe part du chiffre six et pointe vers le neuf. À côté du terme « Mots », il y a la phrase suivante : Six biscuits et trois biscuits font neuf biscuits en tout. À côté du mot « Symboles », on trouve l’équation suivante : six plus trois égale neuf.

Stratégies pour apprendre les faits numériques de base

Il est essentiel d’aider les élèves à élaborer des stratégies efficaces pour apprendre les faits numériques de base en faisant appel à leur raisonnement et en les encourageant à chercher des régularités et des relations entre les nombres. Les stratégies relatives aux faits numériques de base décrites ci-dessous s’appuient sur des connaissances que les élèves ont déjà acquises pour déterminer des faits inconnus. Le fait de savoir, par exemple, ce que font \(2 + 2\) aide les élèves à trouver ce que font \(2 + 3\) (puisque 3 est 1 de plus que 2, la réponse doit aussi être 1 de plus), ce qui dénote une importante habileté de raisonnement. Les stratégies devraient être enseignées dans un contexte de résolution de problèmes. À cet égard, il faut :

• choisir des problèmes se prêtant à l’utilisation des stratégies enseignées;
• donner aux élèves des occasions de modéliser la stratégie à l’étude;
• faire en sorte que les élèves s’exercent à appliquer la stratégie dans un contexte signifiant.

Les élèves ont besoin de nombreuses expériences pour se familiariser avec le regroupement par dizaines et pour établir des relations entre le nombre 10 et les autres nombres avant de pouvoir élaborer des stratégies relatives aux faits numériques de base. Reconnaître le nombre 10 comme point d’ancrage et définir les relations entre ce repère et les nombres de 0 à 10 est un concept de base pour toutes et tous les élèves. Une solide compréhension de la façon dont les nombres sont reliés à 10 (par exemple, 8 est 2 de moins que 10 et 13 est 3 de plus que 10) leur permettra de découvrir les régularités et les relations entre les nombres lorsqu’on leur présentera les stratégies axées sur les faits numériques de base. Connaître les façons dont les nombres sont reliés les uns aux autres facilitera l’apprentissage des stratégies fondées sur la décomposition des nombres.

Un cadre à dix cases est un outil important qui permet aux élèves de représenter concrètement des nombres de 0 à 10 et leur donne la possibilité d’établir la relation entre 10 et les autres nombres. En remplissant certaines cases du cadre, il est possible de voir les cases vides et de reconnaître globalement le nombre représenté. Les élèves peuvent utiliser un ou deux cadres à dix cases et des jetons pour illustrer des nombres de 0 à 20 (deux cadres à dix cases remplis). En utilisant des jetons de différentes couleurs, les élèves peuvent définir des relations de réunion et voir la façon dont elles se rapportent au nombre 10. S’il y a, par exemple, 8 jetons bleus sur un cadre à dix cases et 6 jetons rouges sur un autre cadre à dix cases, les élèves peuvent saisir que 8 jetons bleus plus 2 jetons rouges donnent 10, plus 4 autres jetons rouges donnent 14. Cette façon de faire permet aux élèves de voir concrètement la décomposition du nombre 6 en \(2 + 4\) et d’effectuer des additions plus facilement (\(8 + 2 = 10\) et \(10 + 4 = 14\)).

Les stratégies présentées plus loin visent à aider les élèves à apprendre les faits numériques de base. Les élèves peuvent s’appuyer sur leurs connaissances antérieures (regroupement par dizaines, utilisation des doubles, 10 comme point d’ancrage) lorsqu’on leur présente ces stratégies et qu’on leur donne des occasions de les appliquer. Les activités et les jeux offrent aux élèves des possibilités d’apprentissage interactif tout en leur procurant un cadre pour s’exercer à appliquer une stratégie particulière. En prenant part à un jeu, elles et ils utilisent des stratégies et les intègrent à leur répertoire.

Les stratégies ci-après ne sont pas présentées selon un ordre particulier. Il arrive que des élèves trouvent certaines stratégies plus utiles que d’autres ou ignorent certaines stratégies au profit de leurs stratégies personnelles. D’autres trouvent plus facile de mémoriser les faits plutôt que de s’appuyer sur une stratégie. Quel que soit le cas, l’objectif premier est d’amener les élèves à bien comprendre l’addition et la soustraction.

Stratégies

« 1 de plus » et « 2 de plus »

Dans les faits numériques de base \(5 + 1 = 6\), \(5 + 2 = 7\), \(7 + 1 = 8\), \(7 + 2 = 9\), l’un des termes de chaque addition est 1 ou 2. La stratégie repose sur l’hypothèse que les élèves se rappellent facilement le nombre qui suit et celui qui vient après.

Au-dessus de la grille onze par onze, il est écrit « un de plus, deux de plus ». Dans le coin en haut à gauche, il y a le symbole plus. Les colonnes et les rangées se chiffrent respectivement de zéro à neuf. La rangée et la colonne zéro se chiffrent de zéro à neuf. La rangée et la colonne un se chiffrent d’un à dix. La rangée et la colonne deux se chiffrent de deux à onze. La rangée et la colonne trois se chiffrent de trois à douze. La rangée et la colonne quatre se chiffrent de quatre à treize. La rangée et la colonne cinq se chiffrent de cinq à 14. La rangée et la colonne six se chiffrent de six à 15. La rangée et la colonne sept se chiffrent de sept à 16. La rangée et la colonne huit se chiffrent de huit à 17. Et la rangée et la colonne neuf se chiffrent de neuf à 18. Les chiffres des colonnes et des rangées de zéro à deux inclusivement sont en caractères gras.

Faits numériques avec 0 (\(1 + 0 = 1\), \(1 - 0 = 1\))

Dans ces faits numériques de base, 0 est l’un des termes de chaque addition et de chaque soustraction. Les élèves généralisent souvent en pensant que la réponse à une addition est nécessairement plus grande et que la réponse à une soustraction est nécessairement plus petite. On peut renforcer la compréhension du concept de la neutralité du zéro dans l’addition et dans la soustraction à l’aide de jeux où l’on fait usage de cartes-éclair et de cubes numérotés.

La grille chiffrée s’intitule Faits numériques de base avec zéro. Dans le coin en haut à gauche, il y a le symbole plus. Les colonnes et les rangées se chiffrent respectivement de zéro à neuf. La rangée et la colonne zéro se chiffrent de zéro à neuf. La rangée et la colonne un se chiffrent d’un à dix. La rangée et la colonne deux se chiffrent de deux à onze. La rangée et la colonne trois se chiffrent de trois à douze. La rangée et la colonne quatre se chiffrent de quatre à treize. La rangée et la colonne cinq se chiffrent de cinq à 14. La rangée et la colonne six se chiffrent de six à 15. La rangée et la colonne sept se chiffrent de sept à 16. La rangée et la colonne huit se chiffrent de huit à 17. Et la rangée et la colonne neuf se chiffrent de neuf à 18. Les chiffres de la colonne et de la rangée zéro sont en caractères gras.

Utilisation des doubles

Dans ces faits numériques de base, le premier terme et le deuxième terme (ou les deux termes) sont les mêmes. Il est avantageux pour les élèves de reconnaître et d’apprendre les doubles. Il n’y a que dix faits numériques liés aux doubles. On peut faire appel à des trucs simples de mémorisation pour apprendre plusieurs doubles :

Double de 3 : un insecte a 3 pattes d’un côté et 3 pattes de l’autre (6)

Double de 4 : une araignée a 4 pattes d’un côté et 4 pattes de l’autre (8)

Double de 5 : les 5 doigts d’une main et les 5 doigts de l’autre main (10)

Double de 6 : une boîte contenant une douzaine d’œufs coupée en deux, 6 d’un côté et 6 de l’autre (12)

Double de 7 : dans un calendrier, il y a 7 jours dans une semaine et 14 jours dans deux semaines

Double de 8 : il y a 8 crayons de couleur dans une rangée de boîte de crayons de couleur et 16 crayons de couleur dans deux rangées.

La grille chiffrée s’intitule Utilisation des doubles. Dans le coin en haut à gauche, il y a le symbole plus. Les colonnes et les rangées se chiffrent respectivement de zéro à neuf. La rangée et la colonne zéro se chiffrent de zéro à neuf. La rangée et la colonne un se chiffrent d’un à dix. La rangée et la colonne deux se chiffrent de deux à onze. La rangée et la colonne trois se chiffrent de trois à douze. La rangée et la colonne quatre se chiffrent de quatre à treize. La rangée et la colonne cinq se chiffrent de cinq à 14. La rangée et la colonne six se chiffrent de six à 15. La rangée et la colonne sept se chiffrent de sept à 16. La rangée et la colonne huit se chiffrent de huit à 17. Et la rangée et la colonne neuf se chiffrent de neuf à 18. Tous les chiffres suivant la diagonale à partir de zéro sont en caractères gras.

Les voisins des doubles ou les doubles plus 1 (\(5 + 4\) peut être perçu comme \(4 + 4\), et 1 de plus)

Dans ces faits numériques de base, un des termes de l’addition est 1 de plus que l’autre terme. Les élèves peuvent apprendre à reconnaître que, dans ces additions, la réponse est la même que le double du nombre le moins élevé plus 1 (\(5 + 4 = 4 + 4 + 1\)). Les élèves doivent bien maîtriser les doubles avant de pouvoir utiliser cette stratégie de manière efficace.

Regroupement par dizaines (\(8 + 4 = 8 + 2 + 2 = 12\), \(9 + 5 = 9 + 1 + 4 = 14\))

Dans ces faits numériques de base, l’un des termes est 8 ou 9. Selon le cas, les élèves ajoutent 1 ou 2 provenant de l’autre terme pour obtenir 10, et ajoutent ce qui reste de cet autre terme. On devrait donner aux élèves de nombreuses occasions d’utiliser un cadre à dix cases afin que le regroupement devienne un automatisme.

Dans une question comme \(8 + 5\), par exemple, les élèves peuvent obtenir 10 en additionnant 8 plus 2 (pris du 5), et additionner ensuite le 3 qui reste pour faire 13. Une fois que ces faits sont solidement acquis, il devient beaucoup plus facile pour les élèves de se servir de plus grands nombres, comme \(18 + 5\). En sachant que \(18 + 2\) font 20, il ne leur reste qu’à ajouter le 3 restant pour faire 23. (Cette propriété de l’addition se nomme l’associativité.)

Commutativité (\(1 + 2 = 2 + 1\))

Les élèves qui reconnaissent la propriété de commutativité de l’addition peuvent réduire de moitié la quantité de faits numériques à apprendre. La représentation visuelle de faits comme \(3 + 2\) et \(2 + 3\) aide les élèves à saisir cette relation.

La soustraction comme opération inverse de l’addition pour les faits numériques de base ayant une somme allant jusqu’à 20

Les élèves qui connaissent bien les additions et qui comprennent que la soustraction est l’opération inverse de l’addition, peuvent utiliser ces connaissances pour maîtriser les soustractions correspondantes (si \(5 + 2 = 7\), il s’ensuit que \(7 - 5 = 2\)). Prenons, par exemple, le problème suivant : Julien a 6 billes dans son sac. Georges lui en donne d’autres. Julien a maintenant 14 billes. Combien de billes Georges a-t-il données à Julien? En voyant ce problème, l’élève pense : Quel nombre additionné à 6 donne 14? Ainsi, les faits d’addition qui lui sont familiers l’aident à trouver le terme inconnu dans la phrase mathématique.

La soustraction sous l’angle de l’addition

Les élèves ont plus de difficulté à soustraire les grands nombres. Il peut leur être utile de se rendre compte que des faits comme \(17 - 13\) peuvent être résolus en comptant à partir de 13 jusqu’à 17.

« 1 de moins » et « 2 de moins »

Ces faits de soustraction ont un terme de 1 ou de 2 de moins que l’autre terme. Les élèves peuvent habituellement compter à rebours pour les faits numériques les plus faciles, comme n’importe quel nombre auquel on soustrait 0, 1 ou 2.

Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6^e année, p. 14 à 20.