B1.6 Utiliser des schémas pour représenter et résoudre des problèmes de partage équitable d’un tout pouvant comprendre jusqu’à 20 éléments entre 2, 3, 4, 5, 6, 8 et 10 personnes, incluant des problèmes dont le résultat est un nombre naturel, un nombre fractionnaire ou une fraction, et comparer les résultats.
Activité 1 : la collation spéciale
Les élèves de la classe doivent préparer une délicieuse collation spéciale. À chaque table, le personnel enseignant a placé différents aliments avec des bols et des couteaux en plastique pour les couper en portions si nécessaire. Il doit y avoir un partage équitable des aliments dans chaque bol. En partageant les aliments entre un certain nombre de bols, que remarques-tu?
Exemple 1
Jonas et Hadi sont responsables de partager de façon équitable les bananes. Il y a 6 bols et 8 bananes.
Stratégies
Modèle de surface
Il y a 6 bols et 8 bananes, donc sur une feuille quadrillée je trace 8 rectangles. Ces rectangles représentent 1 banane complète. Je distribue les bananes dans les bols.

Il reste 2 rectangles, soit 2 bananes complètes. Je dois couper les 2 bananes et partager les morceaux dans les 6 bols. Si je partage les bananes en 3 parties égales, soit en tiers, je pourrai déposer un morceau dans chaque bol.
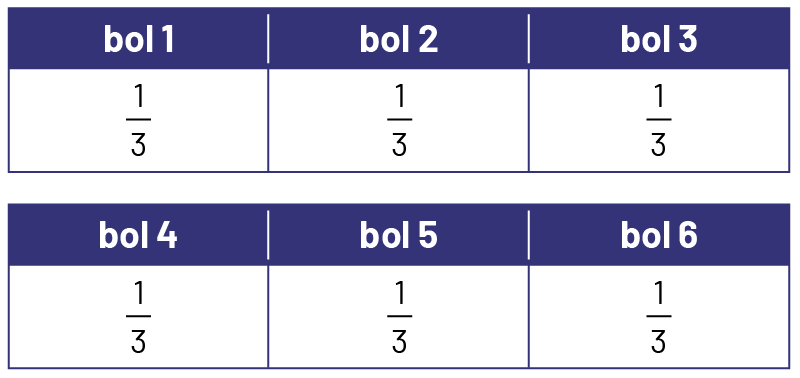
Le partage sera équitable si dans chaque bol, Jonas et Hadi déposent les parties équivalentes de 1 banane complète et \(\frac{1}{3}\) de 1 autre banane.
Exemple 2
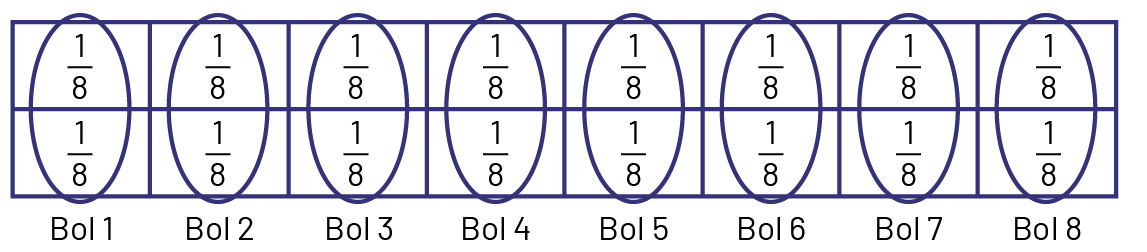
Kamal et Maria sont responsables de partager de façon équitable 2 réglisses dans 8 bols. Par la suite, les 2 élèves aideront à assembler toute la collation spéciale.
Stratégies
Modèle de longueur
2 réglisses doivent être partagées en 8 parties égales. Je plie une bande de papier pour représenter les huitièmes d’une réglisse en la pliant en demis à 3 reprises.
Ceci fait 8 parties égales, ou \(\frac{8}{8}\). Ensuite, on coupe la réglisse en 8 parties égales. En tout, il y a 8 fois \(\frac{1}{8}\) de réglisse. Je répète ceci avec une autre bande de papier, car il y a 2 réglisses. Chaque bol aura \(\frac{2}{8}\) de réglisse.
Source : En avant, les maths!, 3e année, CM, Nombres, p. 3-5.
Activité 2 : la fraction comme division
Exemple 1
Lors d’une fête de fin de saison, les 8 joueurs d’une équipe de soccer doivent se partager 5 sous-marins. Si le partage doit être équitable, quelle portion de sous-marin chaque joueur recevra-t-il?
Réponse possible :
Chaque sous-marin est séparé en 8 morceaux.

On donne un 1er morceau (\(\frac{1}{8}\) de sous-marin) à chacun des 8 joueurs. Puis, on leur donne un 2e morceau (\(\frac{1}{8}\) de sous-marin), et ainsi de suite, jusqu’au 5e morceau. Donc, chacun des joueurs recevra \(\frac{5}{8}\) d’un sous-marin.
Exemple 2
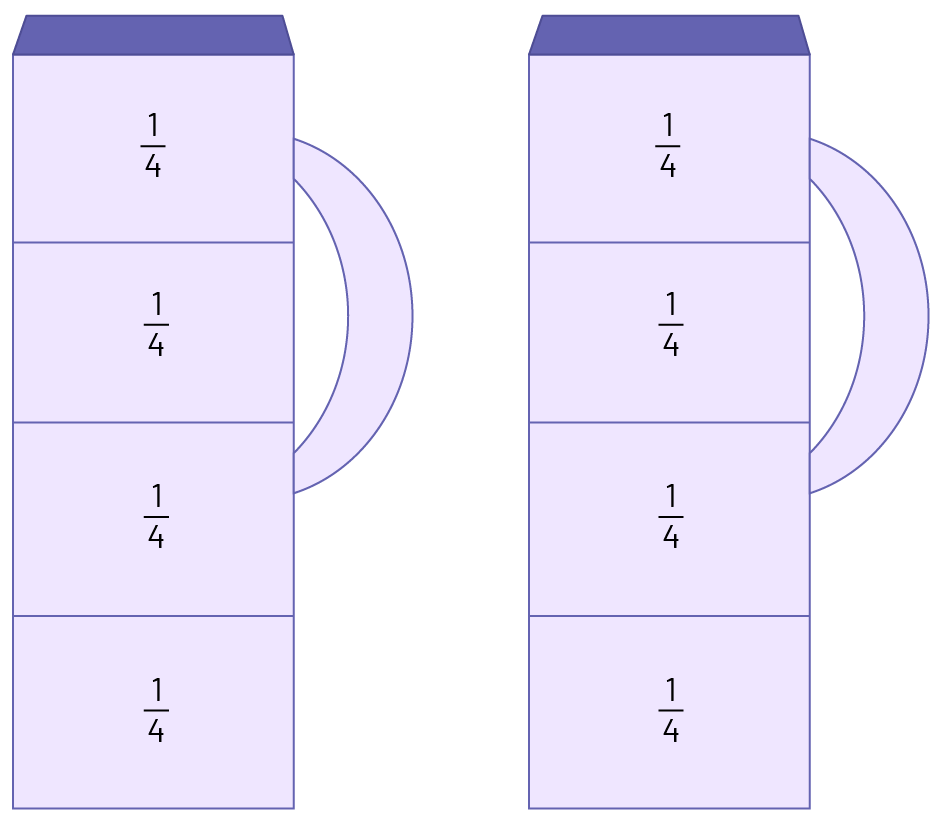
Au restaurant de Lili, 2 litres de sirop d’érable doivent être partagés équitablement dans 8 contenants. Quelle quantité de sirop y aura-t-il dans chaque contenant?
Réponses possibles :
2 litres partagés en 8 contenants, ça veut dire 2 litres divisés par 8 ou \(\frac{2}{8}\).
1re stratégie :
Séparer chacun des 2 litres en 4 parties (en quarts) pour en avoir 8. Donc, chaque contenant contiendra \(\frac{1}{4}\) de litre de sirop.
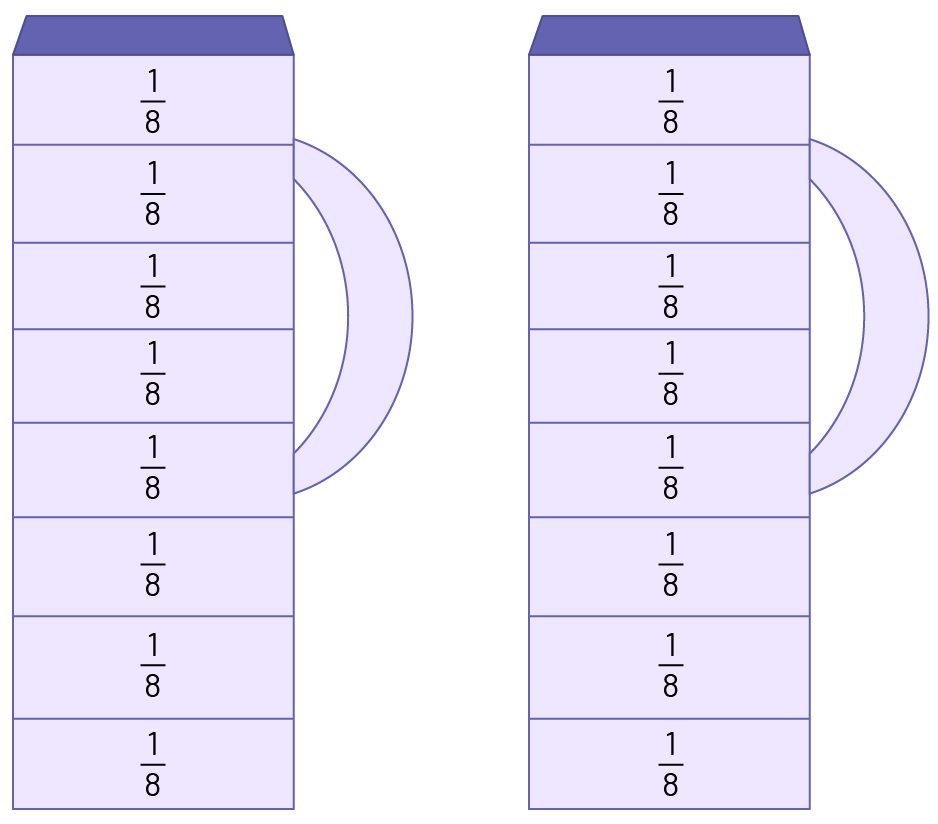
2e stratégie :
Séparer chacun des 2 litres en 8 parties (en huitièmes). Verser \(\frac{1}{8}\) de litre (du 1er litre) dans chacun des contenants. Verser à nouveau \(\frac{1}{8}\) (du 2e litre) dans chacun des contenants. Donc, chaque contenant contiendra \(\frac{2}{8}\) de litre de sirop.
Source: L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
