B1.6 Compter jusqu’à 10 par intervalle de un demi, de un tiers, de un quart, de un cinquième, de un sixième, de un huitième et de un dixième avec ou sans l’aide d’outils.
Habileté : compter jusqu’à 10 par intervalles de un demi, de un tiers, de un quart, de un cinquième, de un sixième, de un huitième et de un dixième avec ou sans l’aide d’outils
Les activités qui requièrent de compter les parties d’un tout, une à une, et de les mettre en relation avec le tout développent la compréhension du rôle du numérateur et du dénominateur. De plus, les élèves apprennent que le nom donné à chaque partie est déterminé par le nombre de parties retrouvées dans le tout. Ainsi, lorsqu’un tout est divisé en deux parties équivalentes, il s’agit de demis; lorsqu’il est divisé en trois parties équivalentes, il s’agit de tiers; lorsqu’il est divisé en quatre parties équivalentes, il s’agit de quarts. À partir de cinq parties équivalentes, on ajoute le suffixe ième au nombre de parties pour obtenir des cinquièmes, des vingtièmes, etc. L’élève qui maîtrise le concept de partie d’un tout n’a pas besoin de recréer l’image de la « tarte » pour comprendre, par exemple, que six sixièmes (\(\frac{6}{6}\)) forment un tout. Ainsi, afin d’identifier la fraction représentée ci-dessous, son raisonnement pourrait être le suivant : « Je compte les morceaux (1, 2, 3, 4, 5 et 6) et j’en conclus qu’il s’agit de sixièmes. Puisque cinq (5) parties sont ombrées, je peux affirmer que cinq sixièmes (\(\frac{5}{6}\)) de la figure sont ombrées. »
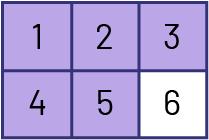
Ce processus les amène aussi à reconnaître qu’une fraction peut correspondre à la somme de fractions unitaires.
Exemple
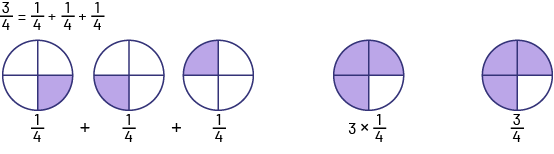image 3 sur 4 est égal à un sur 4 plus un sur 4 plus un sur 4.Un cercle est divisé en 4 quarts dont celui en bas à droite est mauve. Un sur 4.À droite du premier cercle on voit le symbole plus.Un deuxième cercle divisé en 4 quarts dont le quart en bas à gauche est mauve. Un sur 4.À droite du deuxième cercle on voit le symbole plus.Un troisième cercle divisé en 4 quarts dont le quart en haut à gauche est mauve. Un sur 4.À droite de ces 3 premiers cercles, il y a un autre cercle divisé en 4 quarts dont les quarts du haut et celui du bas à gauche sont mauves. 3 multiplié par un sur 4.Il y a un dernier cercle divisé en 4 quarts dont les quarts du haut et celui du bas à gauche sont mauves. 3 sur 4.
Les élèves qui ont compté, par exemple, des parties équivalentes de touts peuvent expliquer que le dénominateur représente ce qui est compté (par exemple, des sixièmes) et que le numérateur représente le nombre de parties.
Il est important pour les élèves de comprendre que plus le tout est fractionné, plus ses parties sont petites.
Exemple
Les quarts d’un tout sont plus gros que les dixièmes du même tout.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 33-35.
Les fractions peuvent décrire des quantités plus grandes qu’un tout. Par exemple, 5 tiers signifie qu’il y a 1 tout (ou 3 tiers) et 2 tiers supplémentaires.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Connaissance : fraction unitaire
Toute fraction dont le numérateur est 1 (par exemple, \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{4}\)). Chaque faction peut être décomposée en des fractions unitaires (par exemple, \(\frac{3}{4}\) est trois fois un quart, ou \(\frac{3}{4} = \frac{1}{4} + \frac{1}{4} + \frac{1}{4}\)).
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.