B1.6 Arrondir les nombres décimaux au dixième près, dans divers contextes.
Activité 1 : le raccourci
Partager la mise en situation suivante aux élèves :
Youssef déménage dans un nouveau quartier et débute à une nouvelle école. Il vit près de l’école et se rendra à pied. Afin de trouver le trajet le plus court, il parcourt différentes routes.
Demander aux élèves d’arrondir les kilomètres parcourus pendant les 4 trajets au dixième près afin de déterminer la meilleure route à prendre.
Trajet 1 : 1,88 km
Trajet 2 : 1,79 km
Trajet 3 : 1,96 km
Trajet 4 : 1,85 km
Exemple
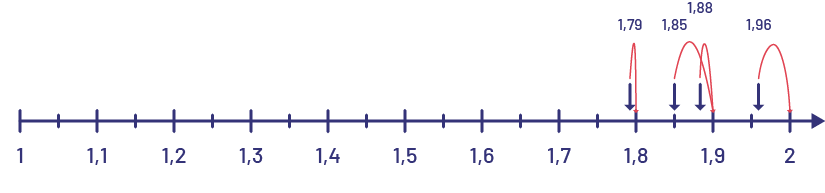image Une droite numérique de un à 2, à intervalles réguliers de zéro virgule un.Une flèche part du tiret un virgule 9 et fait un bond jusqu’à un virgule 88.Une flèche part du tiret un virgule 8 et fait un bond jusqu’à un virgule 79.Une flèche part de 2 et fait un bond jusqu’à un virgule 96.Une flèche part de un virgule 9 et fait un bond jusqu’à un virgule 85.
J’estime que la meilleure route est le trajet 2 puisqu’elle est environ 0,1 ou 0,2 km plus courte que les 3 autres trajets.
Source : adapté de En avant, les maths!, 5e année, CM, Nombres, p. 3.
Activité 2 : la station-service
Présenter la mise en situation suivante aux élèves :
Yassim travaille dans une station-service. Il doit afficher le prix de l’essence sur le panneau extérieur.
Voici les prix de la semaine qu’il a reçus de la propriétaire de la station :
Lundi : 149,84 / l
Mardi : 148,59/ l
Mercredi : 149,85/ l
Jeudi : 151,21/ l
Vendredi : 150,38/ l
Samedi : 148,02/ l
Dimanche : 150,66/ l
Présenter l’exemple du panneau extérieur ci-dessous et générer une discussion à ce sujet avec les élèves.
Demander aux élèves de répondre à la question qui suit :
Quel prix Yassim devra-t-il afficher sur le panneau extérieur chaque jour de la semaine?
Amener les élèves à observer que les prix d’essence sont arrondis au dixième près.
Permettre aux élèves d’utiliser la stratégie de leur choix pour résoudre le problème.
Poser des questions aux élèves telles que :
- Quelle stratégie peut-on utiliser pour arrondir les nombres décimaux ci-dessus? Comment le sais-tu?
- Pourquoi arrondir les nombres? Justifie ta réponse.
- Selon toi, devrait-on arrondir les nombres à la hausse ou à la baisse dans cette mise en situation? Pourquoi?