La vue d'ensemble

À vue d'oeil...

Un remaniement des guides d'enseignement efficace en mathématiques

FrançaisEnglish

B1.3 Comparer et ordonner des nombres entiers, des nombres décimaux et des fractions, séparément et en les combinant, dans divers contextes.

Habileté : comparer et ordonner des nombres entiers

Le signe positif ou négatif indique si le nombre est supérieur ou inférieur à 0. Ainsi, si le nombre est positif, ce dernier sera placé à la droite du 0 sur une droite numérique horizontale ou par-dessus le 0 sur une droite numérique verticale. Si le nombre est négatif, il sera placé à la gauche du 0 sur une droite numérique horizontale ou sous le 0 sur une droite numérique verticale. Le nombre repère pour les nombres entiers est donc toujours 0.

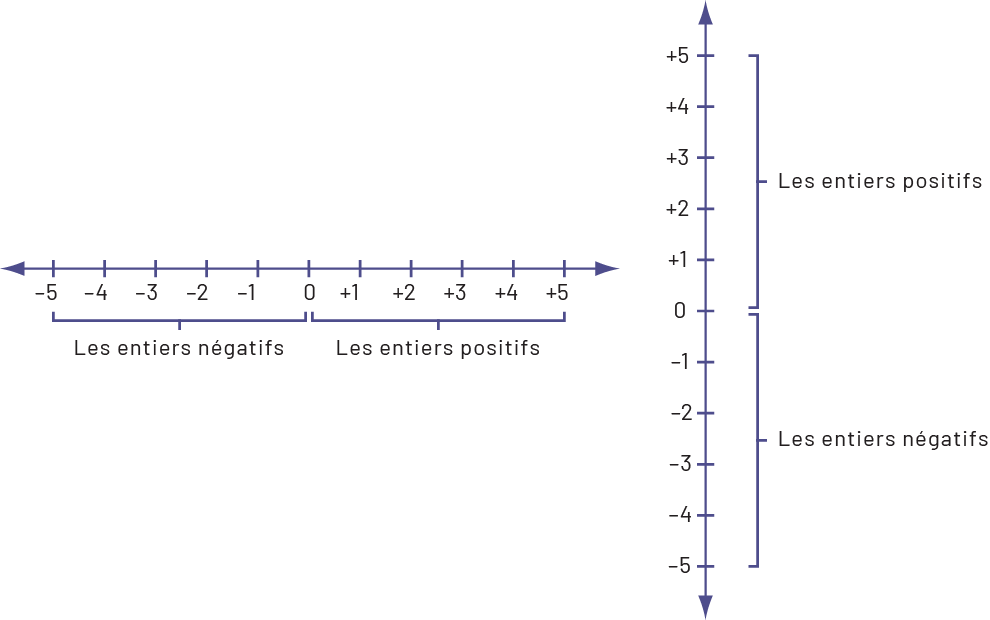Deux droites Deux droites numériques sont présentées côte à côte : l’une est horizontale, l’autre est verticales. Toutes deux sont graduées de moins cinq à plus cinq. Les chiffres de moins cinq à zéro sont les entiers négatifs, tandis que les chiffres de zéro à plus cinq sont les entiers positifs.

Un nombre entier est plus grand qu’un autre nombre entier s’il est placé à sa droite sur une droite numérique horizontale ou au-dessus de celui-ci sur une droite numérique verticale.

Par exemple, \( 8 > 2\) et \((- 2)\; > (- 6)\).

Une droite numérique est graduée de moins sept à plus neuf. Les chiffres suivants sont encerclés en rouge : moins six, moins deux, plus deux, plus huit.

À l’aide de la droite numérique, il est plus facile de comparer et d’ordonner les nombres entiers puisqu’un nombre ayant plusieurs chiffres ne signifie pas nécessairement qu’il est plus grand (par exemple, (−584) est plus petit que 8). En analysant la droite ci-dessus, on peut placer les nombres en ordre croissant ((−6), (−2), 2 et 8) ou en ordre décroissant (8, 2, (−2) et (−6)).

Sur la droite numérique, la valeur absolue d’un nombre est sa distance par rapport à zéro. Par exemple, la valeur absolue de (−3) et 3 est 3 puisque 3 unités séparent les deux nombres de 0.

Une droite numérique est graduée de moins six à six. Au-dessus, il y a deux accolades : la première va de moins trois à zéro et indique trois, et la deuxième va de zéro à trois et indique trois.

Source : Réduction des écarts de rendement, 9e année, p. 11.

Habileté : comparer et ordonner des nombres décimaux

La relation d’ordre est basée sur la comparaison de nombres. Une des grandes forces de la notation décimale, c’est la rapidité avec laquelle il est possible, grâce au concept de valeur de position, de comparer et d’ordonner des quantités. Par exemple, il est beaucoup plus facile de comparer les nombres \(\frac{1}{8}\)et \(\frac{3}{{40}}\)lorsqu’ils sont exprimés en notation décimale, soit 0,125 et 0,075.

En général, les élèves ont peu de mal à comparer des nombres décimaux ayant le même nombre de décimales (par exemple, \(0,341 < 0,462\)). Ils ont plus de difficulté à comparer des nombres ayant un nombre différent de décimales (par exemple, 1,34 et 1,275). Certains ont tendance à comparer ces nombres sans la virgule (par exemple, \(134 < 1275\)) et conclure que \(1,34 < 1,275\). D’autres arrivent à la même conclusion erronée en comparant seulement les nombres à droite de la virgule (par exemple, \(34 < 275\)). Ainsi, un nombre qui comporte plus de chiffres n’est pas nécessairement plus grand.

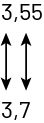
La relation d’ordre doit être abordée en comparant des nombres décimaux dans des situations contextualisées. Par exemple : « Rémi a fait un saut de 3,55 m et Samantha en a effectué un de 3,7 m. Lequel des deux a réussi le plus long saut? » Les élèves peuvent répondre et justifier leur choix s’ils comprennent la valeur de position. La droite numérique est un modèle visuel puissant pour comparer des nombres décimaux. Pour placer 3,7 sur une droite numérique, les élèves peuvent représenter les dixièmes de 3,0 à 4,0. Pour situer 3,55, ils doivent diviser l’intervalle entre 3,5 et 3,6 en dix parties égales, chaque espace représentant un centième. Ils peuvent alors conclure que \(3,55 < 3,7\), donc que Samantha a effectué un plus long saut que Rémi.

Droite Une droite numérique est graduée de trois virgule zéro à quatre virgule zéro par intervalles de dixièmes. L’intervalle entre trois virgule cinq et trois virgule six est gradué par centièmes. Au-dessus de la droite se trouve le chiffre trois virgule 55 qui pointe avec une flèche à l’endroit correspondant sur la droite. Il y a également le chiffre trois virgule sept qui pointe à l’endroit correspondant sur la droite.

Les élèves qui ont acquis un bon sens du nombre peuvent aussi comparer 3,55 m et 3,7 m en remarquant d’abord qu’ils représentent deux sauts supérieurs à 3 m. Ensuite, ils peuvent comparer les dixièmes pour remarquer que le premier nombre compte 5 dixièmes, soit 5 décimètres, tandis que le deuxième en compte 7.

Deux chiffres sont écrits l’un sous l’autre : trois virgule 55 et 3 virgule sept. Une flèche double sens de haut en bas relie les trois, et une flèche double sens de haut en bas relie les décimales.

Le deuxième saut est donc plus long que le premier. Les élèves peuvent aussi, après avoir comparé les unités, penser à 3,7 comme étant 3,70, soit 3 mètres et 70 centimètres. Le nombre 3,55 représente 3 mètres et 55 centimètres. Le saut de 3,7 m est donc plus long que le saut de 3,55 m.

Traditionnellement, on enseignait une procédure où il fallait ajouter un zéro à la fin de 3,7 pour donner deux nombres ayant un même nombre de décimales. Il fallait ensuite comparer les parties décimales, soit 55 et 70, pour conclure que 3,70 était plus grand que 3,55. Certes, l’enseignement de la méthode était accompagné d’une explication, mais on mettait tellement l’accent sur la procédure que l’explication et le concept étaient vite perdus. Il n’est pas surprenant que les jeunes répondent souvent de façon erronée à ce genre de questions. Par exemple, lors d’un test international réalisé auprès d’élèves de 6e année, 87 % ont indiqué que 6 987 est plus grand que 6 879, alors que seulement 52 % ont conclu que 1,05 est plus grand que 1,015 (Brissiaud, 1998). Les élèves qui comprennent le concept de valeur de position n’ont pas besoin d’appliquer une procédure pour comparer des nombres décimaux.

Les problèmes ouverts, qui offrent plus d’une réponse et qui suscitent la réflexion, permettent aux élèves d’approfondir leur compréhension des relations d’ordre. Par exemple :

  • Déterminer trois nombres décimaux situés entre \(\frac{3}{{40}}\) et \(\frac{1}{8}\).
  • Déterminer trois nombres décimaux situés entre 0,555 et 0,623.
  • Déterminer deux nombres situés à un millième de 2,869.

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 54-55.

Habileté : comparer et ordonner des fractions

Relations d’ordre

Il est important que les élèves apprennent à ordonner des fractions en les comparant. L’habileté à ordonner et l’habileté à comparer doivent reposer sur les représentations des fractions que les élèves ont construites. Elles doivent découler de situations de résolution de problèmes qui permettent aux élèves de développer un sens de la valeur d’une fraction. C’est ce sens de la fraction qui permet aux élèves de comparer deux fractions et de conclure qu’une est plus grande que l’autre. Par opposition, l’enseignement qui se fait hors contexte tend à favoriser un apprentissage d’algorithmes qui néglige le sens de la fraction.

Les élèves du cycle moyen ont déjà des idées bien ancrées en ce qui a trait aux propriétés des nombres naturels. Or, lorsqu’ils ou elles commencent à travailler avec des fractions, les élèves font souvent face à un déséquilibre cognitif, c’est-à-dire une impression que ce qui était vrai ne l’est plus. Par exemple, ils ou elles ont appris qu’en présence de deux nombres naturels, le plus grand nombre indique une quantité plus grande. Ils ou elles tentent de transférer leurs connaissances et leurs compétences aux fractions. Ainsi, en voulant comparer \(\frac{1}{6}\) et \(\frac{1}{3}\), certains élèves croient que \(\frac{1}{6}\)est plus grand que \(\frac{1}{3}\), puisque 6 est plus grand que 3. Ils se sentent en déséquilibre s’ils se font dire qu’ils ont tort. Pour éviter de telles situations, l’apprentissage doit reposer sur un regard analytique de la fraction plutôt que sur un automatisme ou un algorithme.

Les activités qui amènent les élèves à comparer et à ordonner les fractions doivent favoriser la construction du sens de la fraction. Pour comparer des fractions, il est rarement nécessaire de chercher un dénominateur commun. Ainsi, il existe de nombreuses stratégies qui permettent de comparer des fractions. Généralement, la première stratégie apprise consiste en l’utilisation d’une représentation concrète ou semi-concrète des fractions en jeu. On peut recourir à cette stratégie, peu importe l’occasion. On peut aussi comparer les numérateurs si les dénominateurs sont identiques, ou comparer les dénominateurs si les numérateurs sont identiques. L’utilisation de fractions repères est une autre stratégie efficace.

Il est important de travailler à fond la comparaison des fractions avant l’équivalence des fractions. En effet, celle-ci est très complexe et la comparaison sert d’élément catalyseur à la compréhension des fractions équivalentes.

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 44-45.

Habileté : comparer des nombres exprimés sous différentes formes

Les élèves du cycle moyen doivent comprendre les relations entre diverses notations d’une quantité, par exemple, les liens qui unissent des nombres décimaux équivalents et des fractions équivalentes. Les élèves doivent reconnaître qu’un nombre décimal est une fraction ou un nombre fractionnaire dont le dénominateur est un multiple de 10 (10, 100, 1 000, 10 000, etc.). Par exemple, le nombre 0,5 est équivalent à la fraction \(\frac{5}{{10}}\) et le nombre 2,63 est équivalent au nombre fractionnaire 2 \(\frac{{63}}{{100}}\). Des modèles tels que les grilles de \(10\; \times \;10\) permettent aux élèves de visualiser les liens entre la fraction correspondante et le nombre décimal correspondant.

Exemple

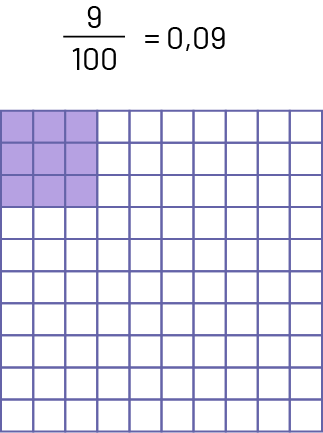
Une grille de cent carrés unitaires présente les neufs carrés du coin supérieur gauche en violet, tandis que les autres carrés sont blancs. Au-dessus de la grille il est écrit : neuf sur cent égale zéro virgule zéro neuf.

En maîtrisant bien cette relation, les élèves sont en mesure d’identifier des fractions et des nombres décimaux équivalents et de choisir la forme la plus propice au contexte. Par exemple, un marchand doit commander la quantité exacte de farine pour répondre à la demande de ses clients. Le premier client nécessite 12,5 kg de farine, le deuxième \(11\frac{3}{4}\) kg, le troisième \(\frac{{15}}{{10}}\) kg et le quatrième \(5\frac{3}{6}\) kg. L’élève qui maîtrise la relation pourrait décider de convertir les fractions en nombres décimaux afin de simplifier le calcul. Donc, \(11\frac{3}{4}\) kg est l’équivalent de 11,75 kg, \(\frac{{15}}{{10}}\) kg est l’équivalent de 1,5 kg et \(5\frac{3}{6}\) kg est l’équivalent de 5,5 kg. Encore une fois, il importe de mettre l’accent sur l’utilisation de modèles pour bien voir les relations entre les fractions et les nombres décimaux plutôt que sur l’apprentissage formel d’une procédure pour effectuer la conversion d’une forme en une autre.

Au cycle moyen, les interventions pédagogiques doivent viser le développement, chez les élèves, d’une plus grande polyvalence avec les nombres. Pour ce faire, le personnel enseignant doit présenter des situations d’apprentissage qui mettent en jeu divers nombres et doit mettre l’accent sur les diverses façons d’écrire ces nombres, tout en faisant réfléchir sur les avantages d’une notation par rapport à une autre. Cette façon de procéder permet aux élèves de développer leur sens du nombre et leur expertise à utiliser les nombres. Il est alors souhaitable que les élèves aient l’occasion de mettre en relation des nombres présentés sous diverses formes, soit des nombres fractionnaires, des nombres décimaux, des fractions, etc.

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 55-56.

Des modèles, particulièrement s’ils sont proportionnels comme la droite numérique, peuvent permettre d’ordonner des nombres, en révéler l’ordre de grandeur et faire ressortir les équivalences entre des fractions, des nombres décimaux et des nombres naturels.

Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.

Connaissance : nombre décimal

Ensemble des nombres décimaux (𝔻)

L’ensemble des nombres décimaux est formé des nombres qui peuvent être exprimés sous forme décimale avec une partie décimale finie (par exemple, 3,72; (–5,1); 0; (–7,0); 12,135 64). Cet ensemble inclut tous les entiers (\(\mathbb{Z}\)), car ils peuvent être exprimés avec une partie décimale (par exemple, \(3\; = \;3,0\)). Il inclut aussi certaines fractions, comme \(\frac{2}{5}\) et \(\frac{3}{{16}}\), puisque \(\frac{2}{5}\; = \;0,4\) et \(\frac{3}{{16}}\; = \;0,187\;5\). Cependant, un grand nombre de fractions sont exclues, comme \(\frac{1}{3}\) et \(\frac{7}{{11}}\), car leur développement décimal nécessite un nombre infini de décimales (\(\frac{1}{3}\; = 0,333\;33\)… et \(\frac{7}{{11}}\; = \;0,636\;363\)…). Il est intéressant de constater que tous les nombres décimaux peuvent être exprimés sous forme de fraction dont le dénominateur est une puissance de 10. (Les puissances de 10 sont 1, 10, 100, 1000… On inclut 1 comme puissance de 10, car, par définition, \(10^{0} \; = \;1\).)

Exemples

\(3,72\; = \;3\;\frac{{72}}{{100}}\; = \;\frac{{372}}{{100}}\)

\( ^- 5,1\; = \; ^- 5\;\frac{1}{{10}}\; = \;\frac{{ ^- 51}}{{10}}\)

\(5\; = \;5,0\; = \;\frac{5}{1}\)

Puisque les nombres naturels sont tous des nombres entiers et que les nombres entiers sont tous des nombres décimaux, on peut représenter la relation entre les ensembles de nombres par le diagramme de Venn ci-dessous.

Dans un cercle vert, on trouve la lettre D, ainsi qu’un plus petit cercle bleu contenant la lettre Z et lequel contient également un plus petit cercle bleu contenant la lettre N.

Note : Il n’existe pas d’ensemble de nombres à virgule. L’appellation nombre à virgule signifie simplement que l’expression du nombre contient une virgule. Ainsi, un nombre à virgule peut être un nombre décimal (par exemple, 0,45), un nombre périodique (par exemple, 0,333…) ou un nombre irrationnel (par exemple, 3,141 5…).

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 42.

La virgule joue un rôle significatif dans la notation décimale. Elle sépare la partie entière de la partie décimale et, de ce fait, indique la position des unités.

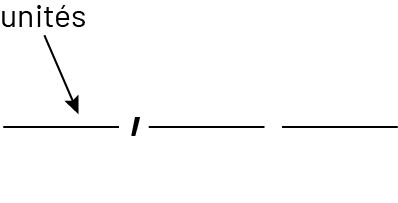
Le schéma se présente comme suit : tiret souligné, virgule, tiret souligné, tiret souligné. Le mot « Unités » pointe avec une flèche vers le premier tiret souligné.

La position des unités définit le tout en fonction duquel sont formés d’une part les dixièmes, les centièmes et les millièmes et d’autre part, les dizaines, les centaines et les milliers. On peut donc dire que l’unité, identifiée par la virgule, est au cœur du système décimal.

schéma Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le mot « unités » est encadré. Les mots « milliers » et « millièmes » sont réunis par un trait, de même que les mots « centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».

Cette reconnaissance du rôle de l’unité est mise en évidence par les préfixes des noms donnés à la valeur de position des chiffres de chaque côté de l’unité. Ainsi, les dixièmes représentent une quantité dix fois plus petite que l’unité.

shéma Le schéma se présente comme suit : milliers, centaines, dizaines, unités, virgule, dixièmes, centièmes, millièmes. Le mot « dixièmes » est encadré. Les mots « milliers » et « millièmes » sont réunis par un trait, de même que les mots « centaines » et « centièmes », ainsi que « dizaines » et « dixièmes ».

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 51.

Connaissance : fraction

Le mot fraction vient du latin fractio qui veut dire « rupture ». Une partie d’un objet brisé peut donc représenter une fraction, car c’est une partie d’un tout. Toutefois, pour déterminer une fraction d’un objet divisé en plusieurs parties, il faut que les parties soient équivalentes. Précisons que lorsqu’il est question de parties équivalentes, il ne s’agit pas nécessairement de formes identiques, bien que celles-ci soient plus faciles à utiliser. Les représentations de un quart \(\left( {\frac{1}{4}} \right)\) dans l’exemple ci-dessous sont basées sur l’aire du tout. Puisque chaque tout a une aire de 16 unités carrées, chaque quart \(\left( {\frac{1}{4}} \right)\) a une aire de 4 unités carrées. Malgré leurs formes différentes, chacun de ces quarts représente une partie équivalente d’un même tout.

Exemple

Six représentations équivalentes de un quart \(\left( {\frac{1}{4}} \right)\) du même tout.

Six grilles de cinq points par cinq points sont disposées en deux rangées de trois. Nous pouvons imaginer que les points sont reliés horizontalement et verticalement pour former des carrés et faciliter la description. Dans la première grille, quatre carrés dans le coin supérieur gauche sont verts. Dans la deuxième grille, les quatre carrés de la première rangée sont en vert. Dans la troisième grille, le premier carré en haut à gauche est en vert, le carré d’à côté est aux trois quarts vert et le carré d’à côté est au quart vert. Le premier carré de la deuxième rangée est vert. Le premier carré de la troisième rangée est aux trois quarts vert et le premier carré de la quatrième rangée est au quart vert. Dans la quatrième grille, le deuxième et le troisième carré de la rangée du haut sont pleinement verts. Le premier et le dernier carré de la rangée du haut sont à moitié vert, et le deuxième et le troisième carré de la deuxième rangée sont à moitié vert. Le tout forme un triangle. Dans la cinquième grille, les trois premiers carrés de la rangée du haut et le premier carré de la deuxième rangée sont verts. Dans la sixième grille, les deux premiers carrés de la rangée du haut et le deuxième de la deuxième rangée sont pleinement verts. Le troisième carré de la rangée du haut et le premier carré de la deuxième rangée sont à moitié verts.

Il est important pour les élèves de comprendre que plus le tout est fractionné, plus ses parties sont petites.

Exemple

Les quarts d’un tout sont plus gros que les dixièmes du même tout.

Deux rectangles sont placés côte à côte. Le premier rectangle est séparé en quatre parties égales, tandis que le deuxième rectangle est séparé en dix parties égales.

Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 33.