E1.2 Construire des solides et décrire les figures planes qui les composent.
Habileté : construire des solides
L’enfant en bas âge s’amuse à construire (avec des Lego, des blocs de bois, etc.), à assembler (des casse-têtes, des formes, etc.) et à décomposer (découpe, plie, déchire des dessins, etc.) différentes formes géométriques. L’enfant se rend compte assez jeune qu’en superposant des blocs, elle ou il crée une tour et qu’en alignant des blocs, elle ou il crée un mur. L’enfant parle de ses constructions comme étant une tour et un mur, car elle ou il les voit comme un tout.
De même, en observant les objets de son environnement, l’élève les décrit d’abord comme un tout et graduellement en nomme les parties et les caractéristiques de certains attributs.
Exemple 1
L’élève dira d’abord : « C’est une maison d’oiseau. » Ensuite, elle ou il dira : « C’est une maison d’oiseau avec un toit pointu, une fenêtre ronde et des murs rugueux. » Lorsqu’on lui demande de reproduire la maison d’oiseau avec des solides, l’élève se rend compte qu’il lui faut différentes sortes de solides. Un peu plus tard, l’élève apprendra à les nommer.
Dans un premier temps, l’enfant construit des maisons sans nommer les solides utilisés. Plus tard, elle ou il construit une copie d’un modèle donné à l’aide de solides. Elle ou il pourra peut-être identifier d’abord les cubes, ensuite les prismes. L’élève pourra ultérieurement identifier tous les solides utilisés.
Voici quelques possibilités de solides qui peuvent être utilisés pour construire la maison d’oiseau :
- un prisme à base triangulaire et un prisme à base rectangulaire;
- deux cubes et deux prismes à base triangulaire;
- cinq prismes à base triangulaire.
Le nombre variera selon la grosseur des solides.
Il est important de laisser les élèves expérimenter et créer librement lorsqu’elles et ils construisent, assemblent ou décomposent des formes géométriques pour la première fois. Il est en outre important de leur permettre d’utiliser divers matériaux ou objets tels que :
- des blocs de bois ou de plastique de formes et de tailles différentes;
- de la pâte à modeler;
- des pailles, des cure-dents, des cure-pipes;
- des tuiles;
- des tangrams;
- des mosaïques géométriques;
- de la ficelle;
- des journaux.
Exemple 2
Pendant les activités guidées, l’élève se rend compte :
- que certaines formes peuvent être assemblées pour créer la même forme, mais de taille différente, par exemple :
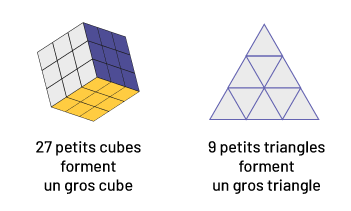
- que certaines formes peuvent être assemblées pour former de nouvelles formes, par exemple :
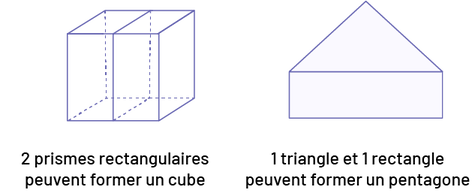image Deux figures. La première image est : « un prisme rectangulaire. » Sous l’image est écrite: « 2
prismes rectangulaires peuvent former un cube. » La deuxième image est un : « pentagone. » Sous le pentagone est écrit
: « un triangle et un rectangle peuvent former un pentagone. »
Les activités de construction, d’assemblage et de décomposition aident l’élève à comprendre plusieurs concepts relatifs au raisonnement géométrique. Par exemple, l’élève approfondit sa compréhension des concepts d’arête et de sommet en construisant des charpentes de solides, et sa compréhension du concept de face en construisant leurs coquilles.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 38-40.
Habileté : décrire les figures planes qui composent un solide
À la maternelle et au jardin d’enfants, l’enfant reconnaît certaines formes géométriques. Elle ou il les reconnaît en les montrant du doigt et en déterminant leur nature. Dès la 1re année, l’élève peut nommer les formes géométriques découvertes à la maternelle ou au jardin d’enfants et plusieurs autres. Elle ou il peut tracer, à l’aide d’un pointeur, d’une baguette ou de son doigt, la ligne fermée qui entoure une figure plane et l’identifier comme étant une ligne brisée ou courbe. De même, elle ou il peut montrer les sommets et les côtés d’une figure plane ainsi que les sommets, les arêtes, les faces et les surfaces d’un solide. L’élève montre ainsi qu’elle ou il associe le vocabulaire approprié aux éléments de la forme géométrique.
Relations entre les formes géométriques
Les activités où les élèves manipulent, construisent et décomposent des objets à trois dimensions leur permettent de voir les relations entre les solides et leurs faces à deux dimensions (par exemple, un cube est composé de faces carrées). Lorsqu’elles et ils comprennent que les figures planes sont des composantes des solides, les élèves sont en mesure de décomposer les objets de leur environnement, d’assembler leurs propres objets et de représenter des objets de façon iconique ou graphique.
Classer des solides permet aux élèves de se concentrer sur les faces à deux dimensions qui les composent. Pendant leurs premières expériences, les élèves utiliseront leurs propres critères ou des critères proposés par le personnel enseignant et découvriront que les solides peuvent être constitués de parties « planes » ou « courbes ». Cette découverte les aidera à comprendre les faces des solides.
La construction de modèles de solides, comme des prismes et des pyramides, constitue une autre expérience d’apprentissage précieuse qui aide les élèves à comprendre que les solides sont faits de faces à deux dimensions. Quand les élèves construisent un modèle, par exemple avec de la pâte à modeler, elles et ils doivent penser à la forme du solide, c’est-à-dire aux formes des différentes faces ou surfaces. Plus tard dans leur parcours scolaire, lorsqu’elles et ils construiront des modèles, les élèves devront visualiser les formes géométriques composant le modèle et l’orientation de celles-ci.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 15-16.