E2.3 Mesurer et tracer des longueurs en centimètres et en mètres en utilisant un instrument de mesure, et reconnaître les conséquences du choix d’un point de départ autre que zéro.
HABILETÉ : MESURER ET TRACER DES LONGUEURS EN CENTIMÈTRES ET EN MÈTRES
« Le nombre de fois que l’unité de mesure est contenue dans la grandeur est la mesure. C’est donc un nombre abstrait qui exprime le rapport entre la grandeur de l’objet et l’unité choisie. »
(Roegiers, 2000, p. 115)
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 86.
Déterminer la longueur au moyen d’un instrument de mesure
L’objet est plus court que l’instrument :
- Zéro comme point de départ : la mesure est la marque sur l’instrument qui est au bout de l’objet.
- Point de départ supérieur à zéro : la mesure est la différence entre la marque sur l’outil et la distance entre zéro et le point de départ.
L’objet est plus long que l’instrument : déplacer l’instrument à répétition sur toute la longueur de l’objet ou de la distance entre deux points (sans espacement ni chevauchement).
- Tous les instruments de mesure, comme les règles et les rubans à mesurer éliminent le besoin de placer et de dénombrer concrètement des unités. Un instrument de mesure répète l’unité sans créer de chevauchement ni laisser d’espaces, et il est gradué (comporte une échelle) pour permettre de garder le compte des unités.
- Une échelle, y compris l’échelle d’une règle, commence au début de la première unité, qui correspond à 0 parce qu’aucune unité n’a encore été mesurée. Au bout de la première unité, l’échelle correspond à 1, car la longueur d’une unité complète a été mesurée. Les nombres sur l’échelle continuent d’augmenter à mesure que chaque unité complète est comptée.
- Une fois le 0 aligné sur l’extrémité d’un objet, l’échelle de l’instrument de mesure garde le compte des unités avec exactitude. Toutefois, la longueur peut être mesurée à partir de n’importe quel point, tant que l’échelle est placée en fonction du point de départ et que le nombre d’unités représente avec exactitude la longueur de l’objet.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
L’exactitude de la mesure dépend de la manière dont on se sert de l’instrument de mesure, c’est-à-dire du respect des modalités d’utilisation de l’instrument. Si l’instrument n’est pas utilisé correctement, la mesure obtenue ne sera pas exacte; elle sera supérieure ou inférieure à la grandeur mesurée. Pour aider les élèves à bien comprendre la bonne façon d’utiliser un instrument de mesure donné, le personnel enseignant peut d’abord modeler son utilisation et déterminer certaines difficultés que certaines et certains élèves pourraient rencontrer. Dans ce qui suit, on présente quelques précisions relatives aux modalités d’utilisation de certains instruments. Pour utiliser correctement une règle, il faut :
- aligner une des extrémités de l’objet sur le zéro ou au début des graduations;
- s’assurer que la ligne de vision de l’autre extrémité de l’objet forme un angle de 90 degrés avec la règle (voir Erreur de parallaxe ci-dessous);
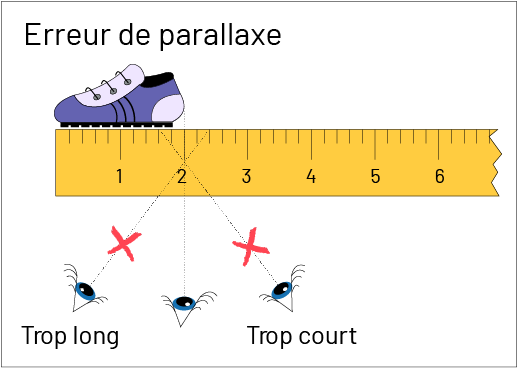
- dénombrer, sur la règle, les unités qui vont d’une extrémité à l’autre de l’objet.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 95.
HABILETÉ : RECONNAÎTRE LES CONSÉQUENCES DU CHOIX D’UN POINT DE DÉPART AUTRE QUE ZÉRO
La distance entre deux extrémités ou la longueur d’un objet reste constante, peu importe où le compte commence sur l’échelle. La mesure correspond au nombre d’unités du début de la longueur et de la fin de la longueur, donc entre les deux extrémités d’une longueur.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Structure associée aux unités de mesure
Le concept de structure associée aux unités de mesure désigne la façon dont ces unités sont organisées pour déterminer la grandeur d’un espace donné, qu’il soit à une, à deux ou à trois dimensions. Il est lié de près au concept d’itération et est à la base de la stratégie de juxtaposition utilisée pour déterminer une mesure. L’exemple ci-dessous précise le sens de ce concept à l’aide d’une situation concrète.
Exemple
Pour déterminer la longueur d’un objet, les unités de mesure doivent être juxtaposées dans un espace à une dimension, sans espace ni chevauchement, de façon à recouvrir la distance entre deux extrémités de l’objet. Le personnel enseignant peut vérifier si les élèves ont bien compris ce concept en leur demandant, par exemple, d’estimer la longueur d’un crayon, puis d’en déterminer la mesure en utilisant un segment de règle.
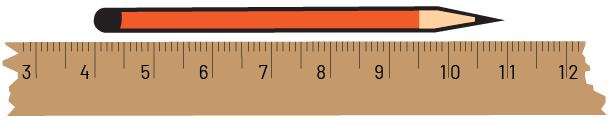
Les élèves qui n’ont pas compris la structure associée aux unités de longueur ont de la difficulté à utiliser cette règle comme instrument de mesure. Plusieurs ont tendance à simplement lire le nombre sur la règle qui correspond à une des extrémités du crayon (11 cm), sans tenir compte du nombre véritable d’unités de longueur que l’on peut dénombrer entre les deux extrémités. Par contre, les élèves qui ont compris ce concept peuvent visualiser une unité de mesure linéaire (le centimètre) disposée plusieurs fois sur toute la longueur du crayon et déterminer le nombre de fois qu’elles et ils la voient. La mesure ainsi obtenue (7 cm) prend alors tout son sens.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 55.
CONNAISSANCE : INSTRUMENT DE MESURE
Instruments de mesure linéaire
- règle, mètre, ruban à mesurer
- règle ou mètre construit à l’aide de cubes emboîtables de 1 cm
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : UNITÉS CONVENTIONNELLES (CENTIMÈTRES ET MÈTRES)
Des unités sont dites conventionnelles parce qu’elles sont employées couramment par un grand nombre de personnes et qu’elles ont, par le fait même, l’avantage de rendre la communication de la mesure claire. Les unités de mesure conventionnelles choisies doivent aussi refléter l’attribut à mesurer. Par exemple, le centimètre ou le mètre pour mesurer des longueurs.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 86.
