E1. Raisonnement géométrique et spatial :
Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure.
Situation d’apprentissage : situe-moi!
Durée totale : 2 h 30 minutes
|
Contexte/Connaissances préalables |
|
Pour décrire les objets, l’élève doit pouvoir les situer en donnant leur position les uns par rapport aux autres. On doit l’amener à voir les relations entre les déplacements possibles dans notre monde ou sur un plan (par exemple, un jeu de dames ou d’échecs, une grille). Pour réaliser l’activité, l’élève doit pouvoir :
L’activité a pour but de permettre à l’élève d’utiliser les expressions à la droite de, à la gauche de, au-dessus de, en dessous de et entre pour décrire la position de figures planes. |
|
Attente |
Contenus d’apprentissage |
|
E1. Raisonnement géométrique et spatial Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.4 Créer et interpréter des cartes simples représentant des lieux familiers. E1.5 Décrire la position relative d’objets divers et les déplacements nécessaires pour passer d’un objet à l’autre. |
Vocabulaire mathématique
à la droite de, à la gauche de, au-dessus de, en-dessous de, entre, grille, case, colonne, rangée
Matériel
- exemples de grilles : jeu de dames, calendriers, grille de 100 (cases 10×10), papier quadrillé
- annexe 2I.1
- annexe 2I.2
Avant l’apprentissage (mise en train)
Projeter l’annexe 2I.1.
Demander à une ou à un élève de montrer une case, une colonne de cases, une rangée de cases. Poser les questions suivantes :
- Peux-tu identifier la figure plane sur la grille?
- Comment peux-tu décrire la position de l’octogone?
- Puisque la figure est seule, faire remarquer que l’on doit décrire sa position en dénombrant les cases, les rangées ou les colonnes.
Dessiner un triangle dans la case à la gauche de l’octogone en disant : « Je dessine un triangle dans la case à la gauche de l’octogone. »
Poser la question : « Comment peux-tu décrire la position de l’octogone sur la grille, maintenant que l’on a ajouté un triangle? »
Souligner que, lorsqu’il y a plus d’une figure, on peut décrire la position d’une figure par rapport à l’autre.
Demander à une ou à un élève de dessiner un cercle dans la case au-dessus du triangle.
Demander à une ou à un autre élève de décrire la position du cercle par rapport au triangle.
Demander à une ou à un élève de dessiner un hexagone dans la case à la droite de l’octogone.
Demander à une ou à un autre élève de décrire la position de l’hexagone par rapport à l’octogone.
Demander à une ou à un élève de dessiner un rectangle dans la case au-dessus de l’hexagone.
Demander à une ou à un autre élève de décrire la position du rectangle par rapport à l’hexagone.
Demander à une ou à un élève de dessiner un carré dans la case au-dessus de l’octogone.
Demander à une ou à un autre élève de décrire la position du carré :
- par rapport à l’octogone;
- par rapport au cercle;
- par rapport au rectangle;
- par rapport au cercle et au rectangle.
Tracer le contour de la figure ainsi formée par l’ensemble des figures planes et demander aux élèves d’identifier la figure mystère.
Exemple de réponse
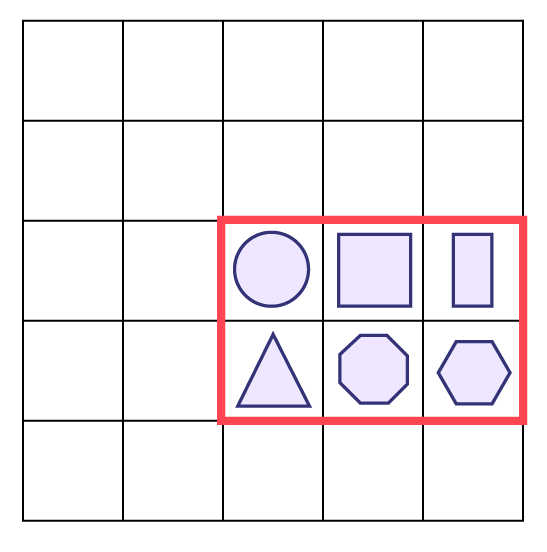 image Une grille de 5 colonnes et 5 rangées. On obtient 25 cases. Dans
la troisième case de la troisième colonne, il y a un cercle, dans la case du dessous, il y a un triangle. Dans la
troisième case de la quatrième colonne, il y a un carré, dans la case en dessous, il y a un octogone. Dans la
troisième case de la cinquième colonne, il y a un rectangle, dans la case en dessous, il y a un hexagone.Une ligne
rouge forme un rectangle autour des cases qui ont une figure.
image Une grille de 5 colonnes et 5 rangées. On obtient 25 cases. Dans
la troisième case de la troisième colonne, il y a un cercle, dans la case du dessous, il y a un triangle. Dans la
troisième case de la quatrième colonne, il y a un carré, dans la case en dessous, il y a un octogone. Dans la
troisième case de la cinquième colonne, il y a un rectangle, dans la case en dessous, il y a un hexagone.Une ligne
rouge forme un rectangle autour des cases qui ont une figure.
La figure mystère est un rectangle.
Pendant l’apprentissage (exploration)
Remettre une copie de l’annexe 2I.2 à chaque élève.
Donner les directives ci-dessous aux élèves :
- Trace, sur ta grille, le contour d’une figure mystère qui contient de quatre à six cases.
- Le rectangle doit être à l’intérieur de la figure mystère.
- Dessine dans chaque case une figure plane.
Leur allouer le temps nécessaire pour accomplir la tâche.
Circuler parmi les élèves et intervenir au besoin en posant des questions. Par exemple :
- Quelle directive peux-tu donner pour que ta ou ton partenaire situe cette figure?
- As-tu une figure qui est entre deux figures?
- As-tu une figure qui est à la fois au-dessus d’une figure et à la droite d’une autre?
- Peux-tu ajouter des figures afin d’avoir une plus grande variété de directives à donner?
Former des équipes de deux élèves et remettre à chaque élève une autre copie de l’annexe 2I.2.
Préciser qu’une ou un élève donne les directives qui permettront à sa ou à son partenaire de reproduire les figures sur la nouvelle grille et de découvrir sa figure mystère.
Directives de l’élève à sa ou à son partenaire :
- Dessine un hexagone dans la case au-dessus du rectangle.
- Dessine un octogone dans la case en dessous du rectangle.
- Dessine un triangle dans la case à la gauche de l’octogone.
- Trace le contour de la figure formée par l’ensemble des figures planes et identifie la figure mystère.
Ensuite, l’autre élève procède de la même façon pour faire découvrir sa figure mystère.
Exemple de réponse
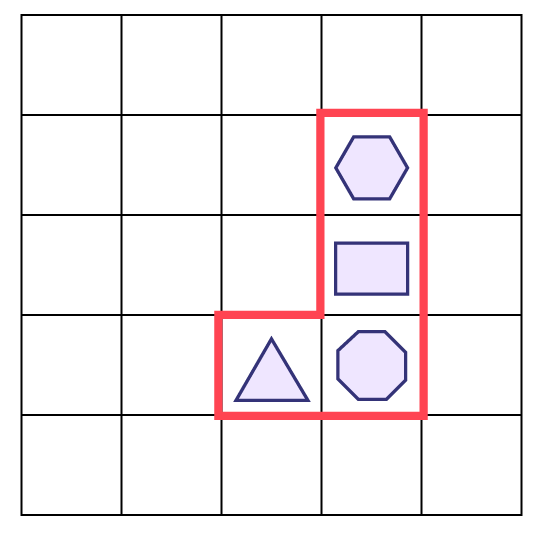 image Une grille de 5 colonnes et de 5 rangées, on obtient 25 cases. Dans
la deuxième case de la quatrième colonne, il y a un hexagone. Dans la case en dessous, il y a un rectangle. Dans la
case en dessous il y a un octogone. À la gauche de l’octogone, il y a un triangle.Une ligne rouge fait le contour de
toutes les cases qui ont une figure, cela forme un « L » à l’envers.
image Une grille de 5 colonnes et de 5 rangées, on obtient 25 cases. Dans
la deuxième case de la quatrième colonne, il y a un hexagone. Dans la case en dessous, il y a un rectangle. Dans la
case en dessous il y a un octogone. À la gauche de l’octogone, il y a un triangle.Une ligne rouge fait le contour de
toutes les cases qui ont une figure, cela forme un « L » à l’envers.
La figure mystère de l’élève est un hexagone.
Après l’apprentissage (objectivation/transfert des connaissances)
Projeter l’annexe 2I.2.
Demander à une ou à un élève de donner ses directives à une ou à un élève d’une autre équipe qui reproduira les figures sur la grille projetée.
S’assurer que l’élève utilise des expressions précises telles que :
- dans la case à la droite de,
- dans la case à la gauche de,
- dans la case au-dessus de,
- dans la case en dessous de,
- entre deux figures, pour décrire avec précision la position de chaque figure plane.
Lorsque les élèves ont trouvé la figure mystère, poser des questions telles que :
- Quelle figure est à la droite de...?
- Quelle figure est à la gauche de…?
- Si une figure est à la droite d’une figure et à la gauche d’une autre, quelle autre expression puis-je utiliser pour décrire sa position?
- Dans quelle autre situation peux-tu utiliser le mot entre pour décrire la position d’une figure?
Laisser des copies des annexes 2I.1 et 2I.2 dans le centre de mathématiques afin que les élèves puissent créer d’autres figures mystères et les présenter à la classe.
Exemples de critères d’évaluation
L’élève :
- décrit de façon précise la position des figures planes;
- nomme la figure qui est à la droite, à la gauche, au-dessus ou en dessous d’une autre figure;
- nomme la figure qui est entre deux figures.
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
Réduire le nombre de cases à remplir ou placer plus de figures planes dans la grille. |
Augmenter le nombre de cases à remplir et exiger que toutes les expressions soient utilisées dans les directives. |
Suivi à la maison
Faire parvenir les expressions étudiées aux parents et leur demander de les utiliser dans des devinettes ou dans des directives.
Exemples
- Tamara, pourrais-tu me nommer l’ustensile qui est à la gauche de l’assiette?
- Jean, pourrais-tu m’apporter la serviette qui est en dessous de la serviette bleue?
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 103-111.
