E1.1 Identifier les propriétés géométriques des rectangles, y compris le nombre d’angles droits, de côtés parallèles et perpendiculaires et d’axes de symétrie.
HABILETÉ : DÉTERMINER LE NOMBRE D’ANGLES DROITS DANS UN RECTANGLE
Les élèves commencent à explorer le concept d’angle dans le contexte d’un angle formé par deux segments sécants. On peut décrire l’angle entre deux segments de droite sécants en tant qu’inclinaison d’un des deux segments par rapport à l’autre à leur point d’intersection.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 22.
L’angle droit est donc une inclinaison perpendiculaire d’un segment par rapport à l’autre segment à leur point d’intersection. L’élève doit repérer l’intersection de deux côtés perpendiculaires d’un rectangle pour découvrir un angle droit. C’est un angle qui a une mesure de 90°. Les élèves peuvent déterminer le nombre d’angles droits dans un rectangle en explorant la rotation d’un des angles droits dans le rectangle. La rotation démontre chaque intersection de deux côtés perpendiculaires du rectangle.

Les élèves peuvent repérer quatre angles droits dans un rectangle.

HABILETÉ : DÉTERMINER LE NOMBRE DE CÔTÉS PARALLÈLES DANS UN RECTANGLE
Les élèves peuvent déterminer le nombre de côtés parallèles dans un rectangle en prolongeant les lignes des paires de côtés opposés. Si la distance qui sépare les lignes d’une paire de côtés opposés reste constante, c’est-à-dire, si les lignes d’une paire de côtés opposés ne se touchent pas, les côtés sont parallèles.
Les élèves peuvent relever deux paires de côtés opposés parallèles.

HABILETÉ : DÉTERMINER LE NOMBRE DE CÔTÉS PERPENDICULAIRES DANS UN RECTANGLE
Les élèves peuvent déterminer le nombre de côtés perpendiculaires dans un rectangle en comptant le nombre de paires de côtés qui se rencontrent ou se coupent à angle droit. Puisque des côtés perpendiculaires forment un angle droit de 90°, il est aussi possible de déterminer le nombre d’angles droits. Ces nombres seront identiques.
Les élèves peuvent repérer quatre paires de côtés perpendiculaires ou quatre angles droits.

HABILETÉ : DÉTERMINER LE NOMBRE D’AXES DE SYMÉTRIE DANS UN RECTANGLE
Les rectangles ont des angles droits de 90º qui permettent la formation de deux axes de symétrie. Les élèves peuvent révéler les axes de symétrie en pliant un rectangle par rapport à un axe de symétrie pour créer des figures identiques. La détermination du nombre d’axes de symétrie peut aussi se faire en créant deux figures identiques à l’aide d’un Mira.
Les élèves peuvent relever deux axes de symétrie dans un rectangle.

CONNAISSANCE : RECTANGLE
Forme géométrique de la famille des trapèzes et des parallélogrammes, qui a les propriétés géométriques suivantes :
- deux paires de côtés congrus;
- quatre angles droits (90°);
- deux paires de côtés opposés parallèles;
- deux diagonales qui se coupent en leur milieu;
- deux axes de symétrie.
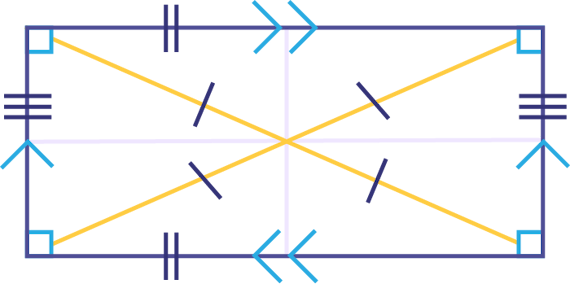 image Un quadrilatère formé de deux ensembles de segments parallèles qui s’intersecte.Les segments
parallèles congrus ,les plus courts, sont identifiés par une seule fléchette, alors que les parallèles congrus les
plus longs sont identifiés par deux fléchettes. La forme est divisée en 8 triangles par deux ensembles de diagonales
marqués par une petite ligne et une ligne verticale et une ligne horizontale.
image Un quadrilatère formé de deux ensembles de segments parallèles qui s’intersecte.Les segments
parallèles congrus ,les plus courts, sont identifiés par une seule fléchette, alors que les parallèles congrus les
plus longs sont identifiés par deux fléchettes. La forme est divisée en 8 triangles par deux ensembles de diagonales
marqués par une petite ligne et une ligne verticale et une ligne horizontale.
Source: Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 36.
CONNAISSANCE : ANGLE DROIT
L’angle droit est une inclinaison perpendiculaire d’un segment par rapport à un autre segment à leur point d’intersection. Les angles sont classés selon les degrés de rotation, puisqu’ils sont essentiellement la mesure d’une rotation autour d’un point.
Un angle droit est un angle qui mesure exactement 90°. L’élève de 4e année n’a pas à connaître la mesure de 90°, cette notion sera introduite formellement en 5e année.

Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 16.
CONNAISSANCE : CÔTÉS PARALLÈLES
Deux côtés parallèles sont des côtés d’une forme géométrique dont la distance qui les sépare reste constante. Les côtés parallèles d’une forme géométrique sont des côtés opposés. Pour représenter une paire de côtés parallèles sur une forme géométrique, une flèche est placée sur chacun des deux côtés. Une deuxième paire de côtés parallèles est représentée par deux flèches, et ainsi de suite.
 image Un quadrilatère formé de deux ensembles de segments parallèles
qui s’intersecte. Les coins sont marqués par des petits carrés. Les segments congrus parallèles, les plus courts, sont
identifiés par une seule fléchette, alors que les parallèles congrus les plus longs sont identifiés par deux
fléchettes.
image Un quadrilatère formé de deux ensembles de segments parallèles
qui s’intersecte. Les coins sont marqués par des petits carrés. Les segments congrus parallèles, les plus courts, sont
identifiés par une seule fléchette, alors que les parallèles congrus les plus longs sont identifiés par deux
fléchettes.
CONNAISSANCE : CÔTÉS PERPENDICULAIRES
Deux côtés perpendiculaires sont des côtés d’une forme géométrique qui se rencontrent ou se coupent à angle droit. Pour représenter deux côtés perpendiculaires, ou un angle droit, sur une forme géométrique, un carré est placé à l’intersection des deux côtés.

CONNAISSANCE : AXE DE SYMÉTRIE
Une figure a une symétrie de réflexion si une moitié de la figure est une réflexion de l’autre moitié par rapport à un axe appelé l’axe de symétrie. Les figures peuvent avoir un ou plusieurs axes de symétrie.
- Un axe de symétrie
- Deux axes de symétrie (ou plus)
- Aucun axe de symétrie
