E1.2 Construire des objets à trois dimensions à partir de vues de face, de côté et de dessus.
HABILETÉ : VISUALISER DES SOLIDES SELON DIFFÉRENTES PERSPECTIVES
Afin de se construire une bonne représentation mentale des solides, les élèves doivent être en mesure de les visualiser aussi bien dans l’espace bidimensionnel des figures planes que dans l’espace tridimensionnel des solides.
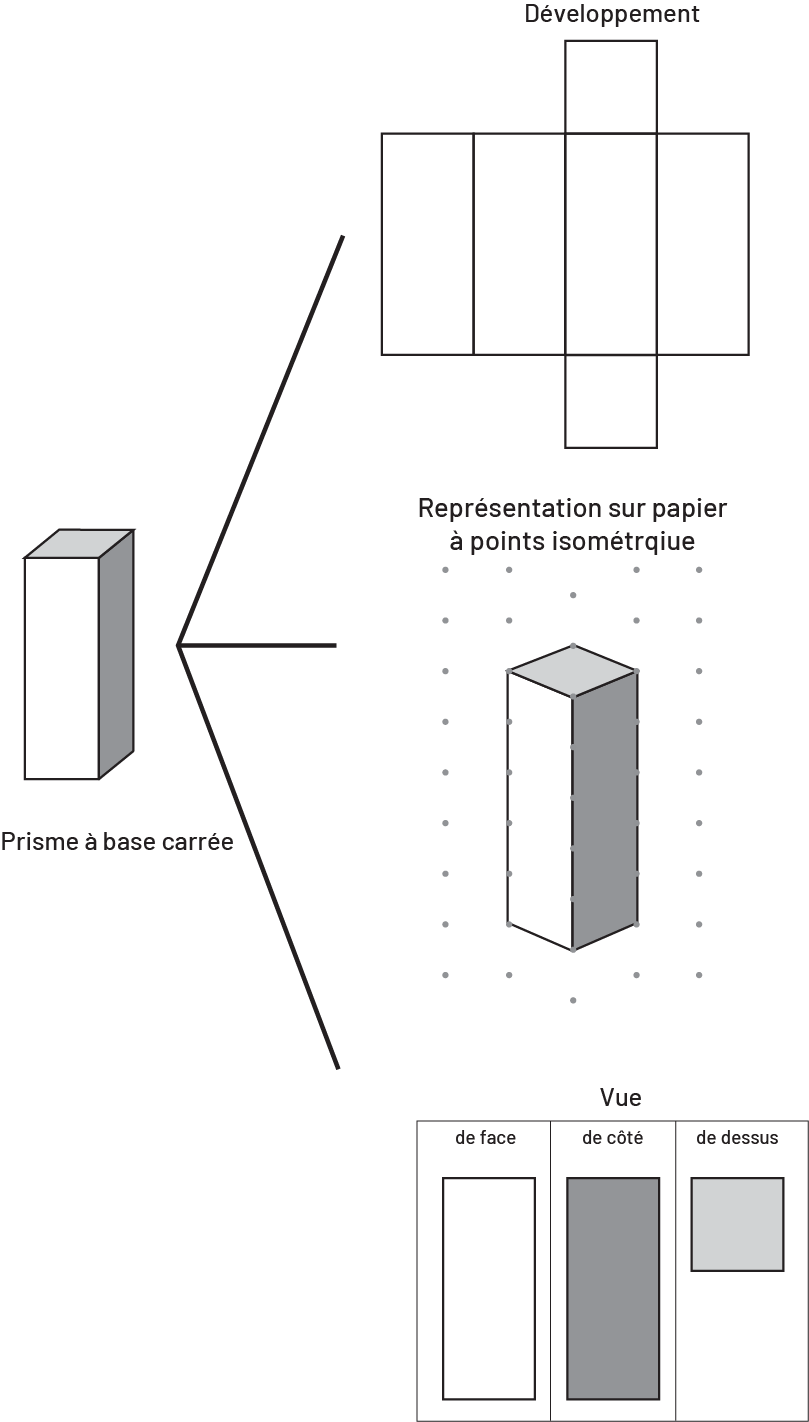Image Il y a un prisme à base carrée. Trois lignes pointent du prisme à un figure différente. La
première est constituée de trois rectangle et deux carrés. Au-dessus de la figure est écrit: développement. La
deuxième est constituée d’un prisme entouré de petits points. Au-dessus de la figure est écrit: représentation sur
papier à points triangulé. La troisième est constitué des trois colonnes. La première contient un rectangle
représentant la figure de face; La deuxième contient un rectangle représentant la vue de côté; La troisième contient
un carré représentant la vue de dessus.
Pour les aider à développer l’habileté à passer d’un espace à l’autre et à consolider leurs connaissances des propriétés des solides, le personnel enseignant peut avoir recours à diverses activités de construction (par exemple, construire un modèle à l’aide de cubes, construire la coquille d’un solide à partir d’un développement donné) et à diverses activités de représentation (par exemple, tracer le développement d’un solide, associer un solide à son développement ou à ses vues de face, de côté et de dessus).
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 29-30.
HABILETÉ : CONSTUIRE DES OBJETS À TROIS DIMENSIONS À PARTIR DE VUES DE FACE, DE CÔTÉS ET DE DESSUS
Les cubes emboîtables peuvent être utilisés pour construire un objet à trois dimensions. En premier, l’élève construit la base du solide à l’aide de la vue de dessus.
Vue de dessus
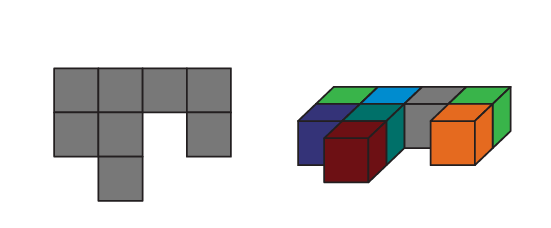
Par la suite, en regardant la vue de côté, l’élève détermine le nombre maximal d’étages de cubes.
Vue de côté
La vue de face permet de déterminer le nombre exact d’étages.
Vue de face
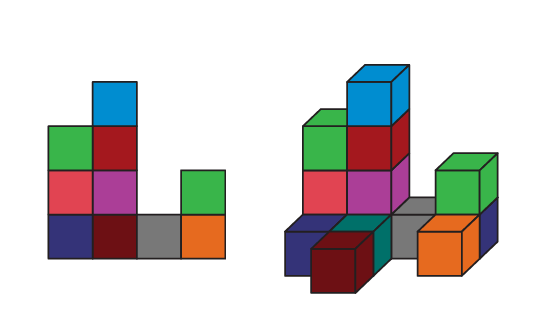
Solide construit à partir des vues de face, de côté et de dessus.
Source : En avant les maths!, 6e année, CM, Sens de l’espace, p.3.
CONNAISSANCE : OBJET À TROIS DIMENSIONS
Un solide géométrique tridimensionnel peut être représenté à l’aide d’une vue de face, d’une vue de côté et d’une vue de dessus.
Source : En avant les maths!, 6e année, CM, Sens de l’espace, p.3.
CONNAISSANCE : VUE DE DESSUS, VUE DE FACE, VUE DE CÔTÉ
Les vues de dessus (plans) ainsi que les vues de face et de côté (élévations) sont des « dessins plats » sans perspective. Ces vues sont utilisées dans le cadre des dessins techniques pour assurer l’exactitude des reproductions en trois dimensions et placer les images dans un tableau.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
Vue de dessus du solide
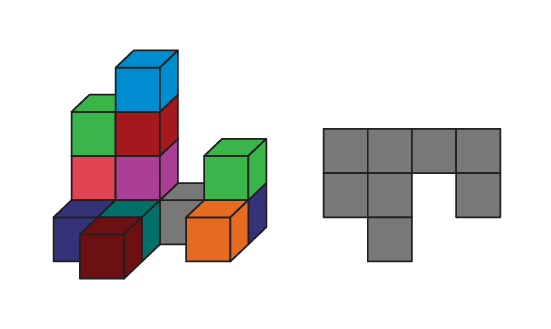
Vue de face du solide
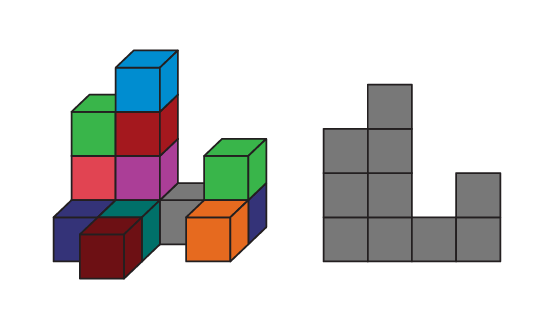
Vue de côté du solide
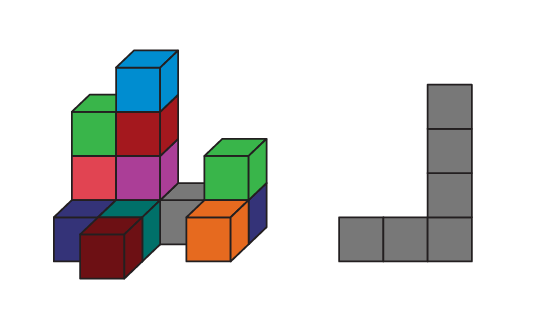
Source : En avant les maths!, 6e année, CM, Sens de l’espace, p.3.