La vue d'ensemble

À vue d'oeil...

Un remaniement des guides d'enseignement efficace en mathématiques

FrançaisEnglish

E1.1 Déterminer les propriétés géométriques des polygones qui forment des dallages ainsi que les transformations géométriques qui se produisent.

ACTIVITÉ 1 : LES DALLAGES AUTOUR DE NOUS

Des planches pour poser du plancher de bois franc.Des gens qui planifient la rénovation d’une cuisine.Un mur de briques.

Cette activité permet aux élèves d’analyser divers dallages et de reconnaître une utilisation pratique et esthétique des propriétés des figures planes et des transformations.

Quelques jours avant l’activité, le personnel enseignant demande aux élèves de reproduire, sur une feuille, un dallage qu’elles et ils voient à la maison (par exemple, carrelage de la salle de bain ou de la cuisine, mur de briques, pavé de l’entrée ou du trottoir). Sur une autre feuille, les élèves dessinent un des motifs du dallage grandeur nature. Le jour de l’activité, le personnel enseignant demande aux élèves de se grouper en équipes de quatre et de comparer les dallages en discutant des figures planes qui les composent, des motifs présents, de la taille des motifs (à l’aide de la deuxième feuille préparée à la maison) et des transformations utilisées pour créer ces motifs. Afin d’alimenter l’échange entre les membres des équipes, le personnel enseignant invite les élèves à discuter des raisons qui peuvent avoir motivé la création de ces dallages (par exemple, formes, couleurs, transformations, matériaux, esthétique, originalité). Par la suite, il demande à chaque équipe de faire part au groupe-classe de certaines constatations en utilisant le mode de présentation de leur choix (par exemple, affiche, présentation orale, discussion).

Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 39-40.

ACTIVITÉ 2 : TOURNE, TOURNE!

Demander aux élèves de vérifier s’il est possible de créer un dallage à partir d’un triangle de l’annexe 6.1 (Les paires de triangles) en utilisant seulement des rotations dont le centre est situé sur un des sommets du triangle.

Note : C’est parfois possible, soit avec les triangles C, D ou E.

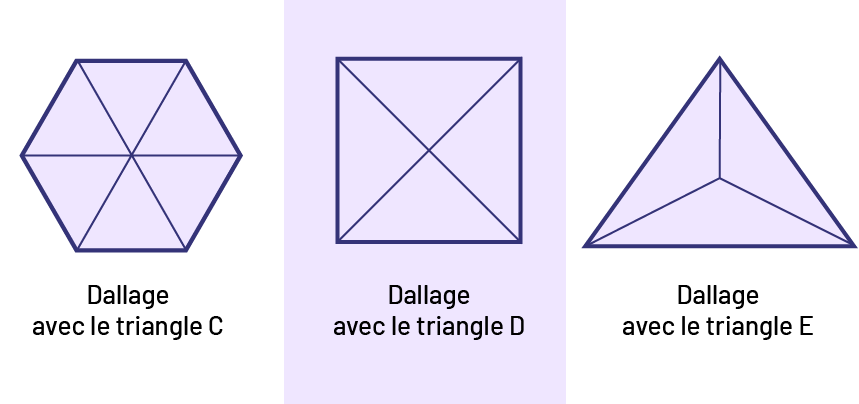Image Un hexagone formé d’un dallage de triangles. « Dallage avec le triangle « C ». »Un carré formé d’un dallage de triangles. « Dallage avec le triangle « D ». »Un triangle formé d’un dallage de triangles. « Dallage avec le triangle « E ».

Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 90.

ACTIVITÉ 3 : Cher Escher

Note : Maurits Cornelis Escher (1898-1972) est un artiste néerlandais rendu célèbre, entre autres, en raison de ses mosaïques qui donnent l’illusion d’une métamorphose (par exemple, Reptiles, 1943) et de ses représentations de mondes impossibles (par exemple, Montée et descente, 1960). Ces œuvres, fondées sur les propriétés des transformations géométriques et sur les lois de la perspective, ont particulièrement fasciné et inspiré les mathématiciennes et les mathématiciens.

Montrer aux élèves quelques-unes des œuvres d’Escher et leur demander d’observer la façon dont l’artiste a réussi à recouvrir le plan. Souligner qu’elles et ils auront l’occasion de créer une œuvre semblable en utilisant les mêmes principes. Demander aux élèves de tracer un grand triangle quelconque sur un carton d’environ 10 cm x 10 cm, de le découper et de déterminer le point milieu de chacun des côtés. Montrer aux élèves la façon de modifier leur triangle pour obtenir une forme originale à partir de laquelle elles et ils pourront créer un dallage :

  • tracer une figure quelconque en partant d’un sommet du triangle et en terminant au point milieu d’un côté adjacent à ce sommet;
Une figure quelconque est tracée en parant d’un sommet d’un triangle
  • découper la figure;
Une figure quelconque est tracée en parant d’un sommet d’un triangle.Cette figure est ensuite découpée.
  • faire subir une rotation à cette figure, en utilisant le point milieu du côté comme centre de rotation, jusqu’à ce que les deux moitiés du côté du triangle soient superposées, et coller les deux morceaux avec du ruban gommé.
Image Une figure quelconque est tracée en parant d’un sommet d’un triangle.Cette figure est ensuite découpée et placée de façon a se qu’elle a subit une rotation.

Si les élèves le désirent, elles et ils peuvent répéter cette démarche en partant de chacun des deux autres sommets. Demander ensuite aux élèves de créer un dallage à partir de la forme obtenue en utilisant des rotations à partir d’un centre de rotation situé sur le point milieu de l’un des côtés. Suggérer d’ajouter des traits à l’intérieur de chacune des formes afin de faire ressortir davantage ce à quoi elles ressemblent (par exemple, oiseau, poisson, feuille) et de colorier leur dallage pour créer un plus bel effet.

Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 91.

ACTIVITÉ À FAIRE À LA MAISON : UN DALLAGE FANTASTIQUE!

Crée un dallage sur lequel on peut voir toutes les figures suivantes :

  • des triangles rectangles congruents;
  • des rectangles congruents;
  • des trapèzes congruents;
  • des losanges;
  • des hexagones.

Colorie ton dallage pour que ta création soit vraiment unique.

Source: L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).