E2.4 Expliquer le théorème de Pythagore en utilisant divers modèles géométriques et se servir du théorème pour calculer la mesure de longueur manquante d’un côté d’un triangle rectangle donné.
Activité 1 : Pythagore : tout un casse-tête!
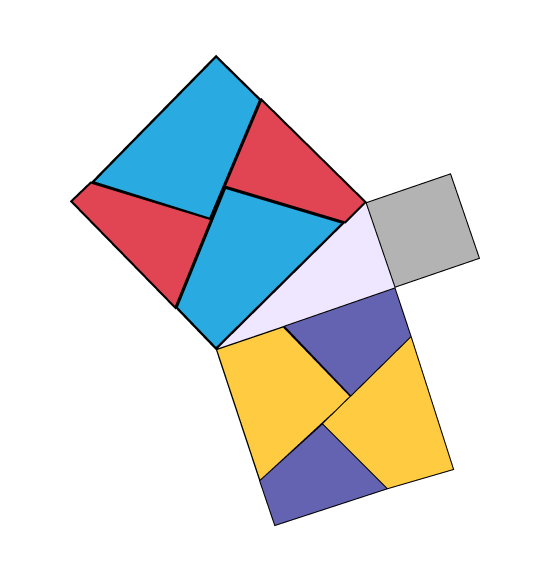Image Un casse-tête composé de divers polygones.Le casse se compose de 2 grands carrés, qui sont
eux-mêmes faits de trapèzes irréguliers. Les 2 carrés sont joints par un triangle et au bout du triangle il y a un
carré.
Distribuer aux élèves le casse-tête ci-dessous ou créer un casse-tête dans un logiciel de géométrie dynamique. Téléverser un document sur une plateforme Web afin que les élèves puissent y consigner leurs observations.
Demander aux élèves d’assembler les pièces du casse-tête en tenant compte des consignes suivantes :
- Choisis le triangle, puis place-le au milieu de ton pupitre.
- Assemble certaines pièces du casse-tête autour du triangle de manière à former un carré sur chacun des côtés de la figure.
- Quelles sont tes observations?
- Fais part de tes observations à une ou à un autre élève ou consigne-les dans le document téléversé.
- Quelles sont les caractéristiques du triangle?
- Si les dimensions du triangle étaient 3 cm, 4 cm et 5 cm, quelle relation pourrais-tu établir en partant de tes observations?
- Si les dimensions du triangle étaient 5 cm, 8 cm et 10 cm, serais-tu en mesure d’établir une relation en partant de tes observations?
- Quelles conclusions peux-tu tirer à la suite de cette activité?
Habiletés à développer relatives à la visualisation spatiale :
- Perception de plans
- Constance des formes
- Perception des positions
- Discrimination visuelle
- Rotation mentale
Source : Guide d’enseignement efficace des mathématiques, de la 7e à la 10e année, p. 14
Activité 2 : problème en lien avec le théorème de Pythagore
- Au moment de préparer la foire régionale, Amarok veut installer un fil de fer à l’extrémité supérieure du poteau principal d’une grande tente de façon qu’il soit bien ancré dans le sol. Si le poteau mesure 16 mètres et qu’elle veut ancrer le fil à 5 mètres de sa base, quelle devra être la longueur minimale du fil de fer?
- Pedro dépose le haut de son échelle de 6 mètres de façon qu’elle arrive directement sur le haut d’un mur. Quelle est la hauteur du mur si le bas de l’échelle est à 3 mètres du bas du mur?
- Maria tient la corde de son cerf-volant qui est 18 mètres au-dessus du sol. Si la corde mesure 23 mètres, à quelle distance se trouve un point qui est directement sous le cerf-volant?