E1.2 Construire des objets et des modèles selon des échelles appropriées, à partir de leurs vues de face, de côté et de dessus, ou de diverses perspectives.
HABILETÉ : CONSTRUIRE DES OBJETS ET DES MODÈLES SELON DES ÉCHELLES APPROPRIÉES, À PARTIR DE LEURS VUES DE FACE, DE CÔTÉ ET DE DESSUS, OU DE DIVERSES PERSPECTIVES
Les représentations bidimensionnelles, si elles sont conçues avec précision et exactitude, peuvent montrer comment des choses sont faites et peuvent être utilisées pour reproduire fidèlement en trois dimensions des objets, petits ou grands, en grandeur réelle ou des modèles à l’échelle.
Les dessins techniques sont des exemples de représentations bidimensionnelles. Dans la vie de tous les jours, la lecture et l’interprétation de ces dessins permettent, par exemple, de parcourir une carte routière, de suivre des instructions d’assemblage d’un meuble ou de construire une composante électronique.
Pour assurer l’exactitude des reproductions en trois dimensions de ces dessins techniques en deux dimensions, dessins qui se doivent d’être à l’échelle, on utilise les vues de dessus (plans) ainsi que les vues de face et de côté (élévations).
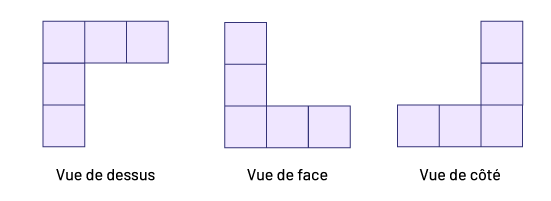Image Vue de dessus:5 blocs sont placés de façon à former un « L » à l’envers.Vue de face :5 blocs
sont placés de façon à former un « L ».Vue de côté :5 blocs sont placés de façon à former un « L » dont l’ouverture
est vers la droite.
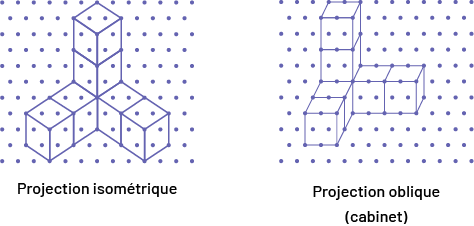
Un dessin en perspective montre trois vues (vues de dessus, de face et de côté) au sein d’une même illustration. Les dessins en perspective sont plus faciles à comprendre que les dessins en élévation et sont privilégiés pour les illustrations dans les domaines technique et scientifique. Cependant, ces vues peuvent déformer les angles et des éléments arrière peuvent être cachés. Le papier isométrique (ou papier triangulé) est utile pour tracer différents types de dessins en perspective, y compris les projections isométriques et les projections obliques (ou cabinet).
Image
Projection isométrique dessinée sur du papier pointillé. Le solide a 7 cubes.Projection oblique d’un solide de 7
cubes, dessiné sur du papier pointillé.
Lorsque l’on veut construire des objets ou des modèles qui sont de bonnes reproductions d’objets déjà existants ou d’objets que l’on examine, comprendre et utiliser les différentes perspectives est un élément essentiel. Mais la maîtrise de l’utilisation d’une échelle appropriée est ce qui permet de faire des reproductions précises et exactes, et de s’assurer d’avoir les longueurs et les proportions voulues.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : ÉCHELLE
Une échelle est un rapport de grandeur qui compare les dimensions réelles aux dimensions du dessin. Selon le type de dessin, les angles peuvent être représentés avec exactitude ou non.
- Les vues de dessus, de face et de côté d’un objet ou d’un espace (dessins en plan et en élévation) présentent les angles réels dans le dessin et montrent toutes les longueurs à l’aide d’une échelle commune. Par exemple, un angle de 60° dans un dessin est de 60° dans un exemple en grandeur réelle, et une échelle de 1 : 100 signifie que 1 cm dans un dessin équivaut à 100 cm dans un exemple en grandeur réelle (ou 1 mm dans le dessin équivaut à 100 mm en contexte réel).
- Les projections isométriques, dessinées sur du papier isométrique, utilisent la même échelle pour toutes les dimensions, y compris la profondeur. Cependant, les angles sont déformés pour créer l’effet de perspective. Ainsi, un angle de 90° dans un exemple en grandeur réelle apparaît comme un angle de 60° dans une projection isométrique.
- Les projections obliques déforment aussi les angles, mais elles utilisent deux échelles pour créer l’effet de perspective. L’échelle « de profondeur » correspond à la moitié de l’échelle « de longueur et de hauteur ». Donc, avec une échelle de 1 : 100, un cube de 1 cm de côté aurait pour dimension, dans une projection oblique, une longueur et une hauteur de 1 cm, mais une profondeur de 0,5 cm.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : VUE DE FACE
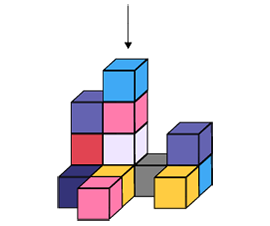
La vue de face (élévation) est un « dessin plat » sans perspective. Cette vue est utilisée dans le cadre des dessins techniques pour assurer l’exactitude des reproductions en trois dimensions.
Vue de face du solide
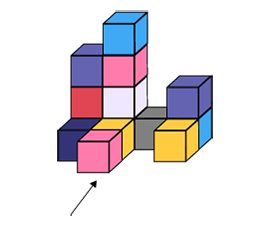
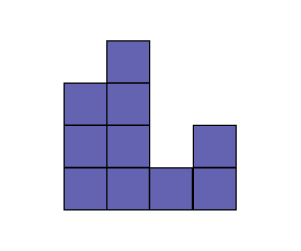
Source : inspiré du CFORP, En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2.
CONNAISSANCE : VUE DE CÔTÉ
La vue de côté (élévation) est un « dessin plat » sans perspective. Cette vue est utilisée dans le cadre des dessins techniques pour assurer l’exactitude des reproductions en trois dimensions.
Vue de côté du solide
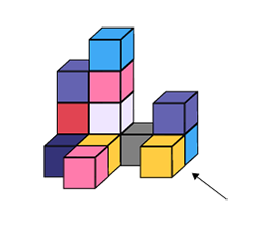
Source : inspiré du CFORP, En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2.
CONNAISSANCE : VUE DE DESSUS
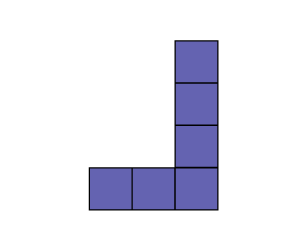
La vue de dessus (plan) est un « dessin plat » sans perspective. Cette vue est utilisée dans le cadre des dessins techniques pour assurer l’exactitude des reproductions en trois dimensions.
Vue de dessus du solide
Source : inspiré du CFORP, En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2.
CONNAISSANCE : PERSPECTIVES
Dessin en perspective
Un dessin en perspective montre trois vues (vues de dessus, de face et de côté) au sein d’une même illustration. Les deux types de dessin en perspective sont la projection isométrique et la projection oblique (ou cabinet).
Projection isométrique
La projection isométrique représente un objet en perspective selon une « vue de coin », de manière que les arêtes principales de l’objet (c’est-à-dire les trois dimensions de l’objet) forment des angles égaux. Dans une projection isométrique, une échelle est appliquée de façon constante à toutes les dimensions de l’objet, par exemple 1 cm = 2 cm pour la longueur, la hauteur et la profondeur.
Projection oblique (projection cabinet)
La projection oblique représente un objet en perspective selon une « vue directe » de l’une de ses faces, de manière que la profondeur soit représentée par des droites obliques (c’est-à-dire selon un angle). Dans une projection oblique, l’échelle « de profondeur » est la moitié de l’échelle « de longueur et de hauteur » (par exemple, si l’échelle pour la hauteur et la longueur est 1 : 2, soit 1 cm = 2 cm, alors l’échelle pour la profondeur est 0,5 : 2, soit 0,5 cm = 2 cm).
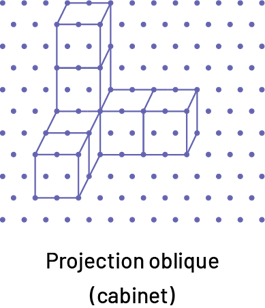
Source : En avant, les maths!, 7e année, CM, Sens de l’espace, p. 2-3.