E1. Raisonnement géométrique et spatial
Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure.
SITUATION D’APPRENTISSAGE 1 : MYSTÉRIEUSES RUINES
Durée totale : 90 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves utilisent des cubes emboîtables pour construire une maquette de ruines qui correspond à un ensemble de vues données.
|
Attente |
Contenu d’apprentissage |
|
E1 Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.2 Construire des objets et des modèles selon des échelles appropriées, à partir de leurs vues de face, de côté et de dessus, ou de diverses perspectives. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à développer leur sens de l’espace et leur habileté à visualiser les objets en trois dimensions;
- à construire la maquette d’un solide à partir de ses vues;
- à établir des liens entre les représentations bidimensionnelles et tridimensionnelles d’un solide;
- à développer et à utiliser des stratégies de résolution de problèmes.
|
Contexte pédagogique |
Préalables |
|
Au cours des années d’études précédentes, les élèves ont exploré, manipulé et classé des solides. Elles et ils ont construit des structures à l’aide de solides à partir d’un modèle donné et construit la charpente et la coquille d’un solide à partir de son développement. Toutes ces activités leur ont permis de développer le sens de l’espace ainsi que l’habileté à visualiser un solide quelconque en deux et en trois dimensions, et à établir des liens entre ses représentations bidimensionnelles et tridimensionnelles. En 8e année, les élèves continuent à développer cette habileté, notamment en explorant les différentes vues (de face, de côté et de dessus) d’un solide. |
La présente situation d’apprentissage permet aux élèves d’approfondir, dans un contexte de résolution de problèmes, leur compréhension des vues et de parfaire leur habileté à visualiser un objet en trois dimensions à partir de ses vues. Les élèves doivent analyser les vues des côtés est, ouest, nord et sud des ruines d’un ancien monument et construire avec le moins de cubes possible une maquette qui correspond à ces vues. Il s’agit d’une tâche d’analyse et de déduction assez complexe qui leur permet de travailler au niveau de l’analyse et de cheminer vers le niveau de la déduction informelle de la pensée géométrique, niveaux décrits par les Hollandais van Hiele. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
vue de côté, vue de face, vue de dessus
Matériel
- annexes 6.3, 6.4, 6.6a et 6.6b
- tableau blanc interactif
- annexes 6.1 et 6.2 (une copie par élève)
- annexe 6.3 (deux copies par élève et une copie par équipe)
- annexes 6.6a et 6.6b (une copie par équipe)
- cubes emboîtables (16 cubes par élève et 100 cubes par équipe)
- grandes feuilles de papier (une par équipe)
- appareil photo numérique (facultatif)
Activité préparatoire facultative
L’annexe 6.9 présente un exemple d’une telle activité. S’en servir au besoin pour vérifier si les élèves ont acquis les préalables nécessaires à la réalisation de la situation d’apprentissage.
Avant l’apprentissage (mise en train)
Durée : environ 30 minutes
Remettre à chaque élève 16 cubes emboîtables et une copie des annexes 6.1 (Modèle 1) et 6.3 (Papier quadrillé). Leur demander de construire, à l’aide de neuf cubes emboîtables, une maquette qui correspond au modèle sur la photo.
Demander aux élèves, une fois leur maquette construite, de dessiner sur le papier quadrillé les cinq vues visibles, soit les vues de gauche, de droite, de devant, de derrière et de dessus. Faire une mise en commun du travail effectué. Demander à des élèves de venir, à tour de rôle, tracer une des cinq vues au tableau ou au tableau interactif. Leur dire de conserver cette maquette afin de la comparer avec la prochaine maquette qu’elles et ils construiront.
Remettre à chaque élève une copie des annexes 6.2 (Modèle 2) et 6.3 (Papier quadrillé). Leur demander d’utiliser les sept cubes qui restent pour construire une maquette qui correspond au modèle sur la photo et de tracer sur le papier quadrillé les cinq vues visibles. Une fois le travail terminé, demander aux élèves de former des équipes de deux et de comparer leurs vues des modèles 1 et 2. Faire une mise en commun de leurs observations.
Les élèves devraient constater que les vues de gauche sont identiques pour les deux modèles et qu’il en est de même pour les vues de droite, de devant et de derrière. Cependant, les vues de dessus des deux modèles sont différentes. Leur demander d’expliquer la raison pour laquelle il est possible de construire deux maquettes qui ont les mêmes vues de côté, mais qui nécessitent un nombre différent de cubes. (Dans le modèle 1, les cubes sont reliés les uns aux autres alors que certains sont détachés dans le modèle 2, ce qui permet d’éliminer des cubes tout en respectant les vues.)
Cette activité prépare les élèves à la mise en situation qui suit. À l’aide des annexes 6.4, 6.6a et 6.6b, la présenter aux élèves.
Mystérieuses ruines
Sur un site archéologique, une équipe de fouilles a mis au jour les ruines d’un très ancien monument. Afin que
les archéologues puissent le reconstituer, un fouilleur a tracé les vues de chacun des quatre côtés (est, ouest,
nord, et sud). Les archéologues veulent faire une maquette des ruines de ce monument avec des cubes d’après les
quatre vues que le fouilleur a tracées. Elles et ils se rendent compte qu’il y a plusieurs dispositions
possibles des cubes qui respectent les vues. Pouvez-vous, à l’aide de cubes emboîtables, construire une maquette
de l’une de ces dispositions? Pouvez-vous en construire une avec le moins de cubes possible?
Vérifier si les élèves comprennent bien la mise en situation et la tâche à effectuer en posant des questions telles que :
- Qui peut m’expliquer ce que sont des ruines (un site archéologique, des fouilles, des vues, une maquette, des dispositions possibles) et en donner des exemples?
- Qui peut m’expliquer la tâche à effectuer dans ses mots?
Pendant l’apprentissage (exploration)
Durée : environ 45 minutes
Former des équipes de quatre élèves. Remettre à chaque équipe environ 100 cubes emboîtables et les quatre vues des
ruines du monument (annexes 6.6a et 6.6b). Leur demander de construire une maquette des ruines qui respecte les vues
tout en tentant d’utiliser le moins de cubes possible.
Note : L’organisation physique et matérielle de la classe peut jouer un rôle important dans la réussite de cette activité. On peut, par exemple, demander à chaque équipe de se regrouper autour de deux pupitres placés côte à côte, sans les chaises. Cette disposition permet aux élèves de se déplacer plus facilement autour des pupitres et de bien se pencher pour observer les vues (voir la photo 1 ci-dessous). On peut aussi mettre à la disposition des élèves une variété de matériel, notamment des feuilles de papier quadrillé (annexe 6.3). Certaines et certains élèves pourraient choisir d’utiliser du papier quadrillé comme stratégie pour les aider à disposer et à aligner les cubes en groupes détachés tout en respectant les vues (voir la photo 2 ci-dessous).
 Image Sur
des feuilles des papiers il y a des modèles de structures en carrés. Sur la table de travail, des modèles ont été
reproduits avec des cubes emboitables.
Image Sur
des feuilles des papiers il y a des modèles de structures en carrés. Sur la table de travail, des modèles ont été
reproduits avec des cubes emboitables.
Allouer suffisamment de temps pour permettre aux élèves d’explorer diverses stratégies de résolution de problèmes et d’en discuter. Circuler parmi les élèves et intervenir au besoin. Porter une attention particulière aux stratégies utilisées et à la composition des maquettes afin de choisir de façon stratégique les équipes qui seront invitées à faire une présentation au moment de l’échange mathématique.
|
Observations possibles |
Interventions possibles |
|
Chaque membre d’une équipe choisit une des quatre vues des ruines et construit la rangée de cubes qui lui correspond. Ensuite, l’équipe construit une maquette en disposant les quatre rangées de façon à former les murs extérieurs d’une structure rectangulaire, sans se rendre compte que deux des murs ont une largeur correspondant à 11 cubes. |
|
|
Une équipe se rend compte qu’il est possible de construire une maquette formée de seulement deux murs extérieurs (par exemple, les vues nord et ouest), puisque la vue de derrière du côté nord correspond à la vue de face du côté sud et que la vue de derrière du côté ouest correspond à la vue de face du côté est. |
|
|
Une équipe élimine plusieurs cubes de chacun des murs extérieurs, mais leur maquette ne respecte plus les vues données. |
|
|
Certaines équipes réussissent à réduire le nombre de cubes en détachant certains cubes des murs extérieurs. |
|
|
Une équipe construit une maquette dans laquelle les cubes sont détachés et placés stratégiquement dans un espace carré de dimensions 9 × 9. |
|
Demander aux équipes de noter leurs stratégies, leurs essais et leurs réflexions sur une grande feuille. Si un appareil photo numérique est disponible, demander aux équipes de prendre une photo de leur maquette.
Note : Dans cette situation d’apprentissage, le nombre minimal de cubes que l’on doit utiliser est 20. On devrait toutefois éviter d’accorder trop d’importance à ce nombre. L’important, c’est que les élèves puissent visualiser la façon d’enlever certains cubes tout en respectant les vues données. La photo 2 montre une maquette possible construite avec 20 cubes. Les annexes 6.7a et 6.7b illustrent, à l’aide de la vue de dessus, d’autres exemples de dispositions possibles.
Après l’apprentissage (objectivation/échange mathématique)
Durée : environ 15 minutes
Demander aux équipes choisies de présenter leur maquette, d’expliquer la stratégie utilisée pour résoudre le problème et de faire part de leurs observations. Leur demander de formuler ces observations en utilisant des termes de causalité ou de conséquence logique. Voici quelques exemples d’observations possibles :
- Lorsqu’on construit un rectangle en utilisant les quatre rangées de cubes qui correspondent aux quatre vues, on obtient une maquette qui ne respecte plus les vues données parce que deux des côtés du rectangle ont alors 11 colonnes de cubes au lieu de 9.
- Puisque la vue du côté sud est simplement la réflexion de la vue du côté nord, alors on peut utiliser une seule rangée de cubes pour représenter les deux vues. C’est la même chose pour les vues des côtés est et ouest.
- Il est permis de détacher les cubes des murs extérieurs parce que les ruines ne sont pas nécessairement composées de cubes reliés les uns aux autres selon une disposition rectangulaire.
Note : Pour les présentations, il peut être assez difficile pour les élèves de déplacer les maquettes à l’avant de la classe. Si les élèves ont pris des photos, elles et ils peuvent les projeter au tableau interactif. Sinon, on peut demander aux élèves de se regrouper autour de la maquette de l’équipe qui présente.
Inviter les autres élèves à réagir à chacune des présentations et à faire part de leurs observations ou de leurs questions. Faciliter le déroulement de l’échange mathématique en posant, au besoin, des questions telles que :
- Qui peut m’expliquer dans ses mots la stratégie utilisée par cette équipe pour construire sa maquette?
- Croyez-vous que leur maquette respecte les vues données?
- Est-ce que d’autres équipes ont utilisé la même stratégie? Avez-vous utilisé le même nombre de cubes?
- Êtes-vous d’accord avec ce que vient de dire cette équipe? Pourquoi?
- Est-ce que quelqu’un a une stratégie qui permet d’enlever d’autres cubes? Peux-tu venir le démontrer?
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
|
Suivi à la maison
Demander aux élèves d’apporter à la maison leurs dessins des vues des modèles 1 et 2 (annexes 6.1 et 6.2). Leur demander d’utiliser des cubes disponibles à la maison pour construire les maquettes qui correspondent aux deux modèles. Au besoin, leur permettre d’apporter des cubes emboîtables à la maison. Leur demander de montrer à un membre de la famille la façon possible de construire deux structures différentes à partir de quatre vues de côté données.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83-91.
SITUATION D’APPRENTISSAGE 2 : DALLES-TU?
Durée totale : environ 100 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves créent des dallages à partir d’un triangle en utilisant une ou deux transformations différentes.
|
Attente |
Contenu d’apprentissage |
|
E1 Décrire et représenter la forme, la position et le déplacement en se servant de propriétés géométriques et de relations spatiales pour s’orienter dans le monde qui l’entoure. |
E1.1 Déterminer les propriétés géométriques des polygones qui forment des dallages ainsi que les transformations géométriques qui se produisent. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves :
- à créer des dallages;
- à visualiser les transformations d’une figure qui permettent de créer un dallage;
- à formuler des hypothèses et à les vérifier;
- à reconnaître certaines propriétés des triangles.
|
Contexte pédagogique |
Préalables |
|
Au cours des années d’études précédentes, les élèves ont développé une compréhension de plusieurs propriétés des figures planes. Elles et ils ont utilisé des transformations comme régularité, et ont aussi appris à décrire et à effectuer différentes transformations telles que la translation, la réflexion et la rotation. Les élèves ont généralement fait la découverte de la propriété de la somme des angles d’un triangle et peuvent maintenant générer un dallage ayant un motif en utilisant la rotation. |
La présente situation d’apprentissage permet aux élèves de consolider leur compréhension des propriétés des triangles et des dallages, de travailler au niveau de l’analyse et de cheminer vers le niveau de déduction informelle de la pensée géométrique du modèle des van Hiele. Elle prépare aussi les élèves à l’étude des dallages réguliers et semi-réguliers. Pour de plus amples renseignements au sujet des dallages réguliers et semi-réguliers, consulter les modules Formes géométriques et Angles sur le site Web atelier.on.ca. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
rotation, translation, réflexion, axe de réflexion, centre de rotation, point milieu, dallage, sommet, degré
Matériel
- mosaïques géométriques
- tableau blanc interactif
- annexe 6.1 (photocopiée sur du carton)
- annexe 6.2 (une copie par équipe)
- ciseaux (une paire par élève)
- bâtonnets de colle (un par équipe)
- petites feuilles (plusieurs demi-feuilles blanches par équipe)
- grandes feuilles de papier (une par équipe)
Avant l’apprentissage (mise en train)
Durée : environ 15 minutes
Revoir avec les élèves la définition de dallage et leur demander d’en créer un à l’aide de mosaïques géométriques ou à l’aide d’un logiciel. Inviter ensuite quelques élèves à montrer leur dallage à la classe ou au tableau interactif. Souligner que le fait qu’il soit possible ou non de créer un dallage avec certaines formes géométriques dépend des propriétés de ces formes.
Discuter avec les élèves de l’importance de l’animatique (animation assistée par ordinateur) dans la production de certaines émissions de télévision, de films et de jeux vidéo. Expliquer que l’effet de mouvement dans ces animations est créé habituellement à l’aide de transformations géométriques effectuées sur une figure ou sur un objet. Ainsi, pour animer à l’ordinateur la construction d’un dallage, la conceptrice ou le concepteur doit connaître les propriétés des figures géométriques et des transformations. Pour aider les élèves à bien comprendre le rôle des transformations dans la construction d’un dallage, montrer l’animation prévue à cet effet dans le module Position et déplacement sur le site Web atelier.on.ca.
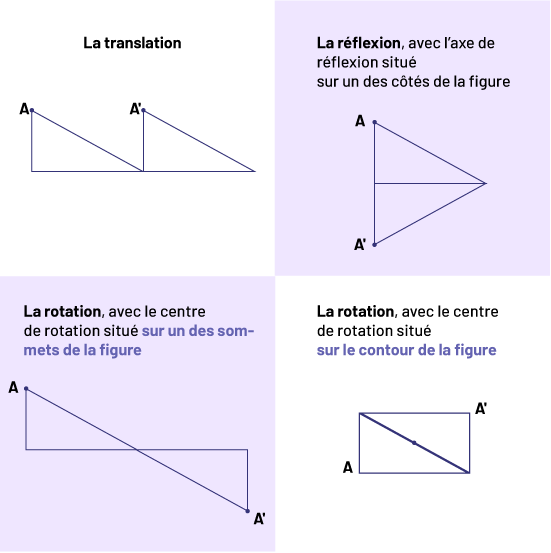
Au besoin, revoir les quatre transformations décrites ci-dessous. S’assurer notamment que les élèves sont capables d’effectuer une rotation lorsque le centre de rotation est situé sur le contour d’une figure.
 Image
Un
exemple de translation, avec un triangle rectangle qui un effectué un glissement vers la droite.Un exemple de
réflexion, avec un triangle rectangle qui est devenu un triangle isocèle aigu.La réflexion, avec l’axe de
réflexion situé sur un côté de la figure.La rotation, avec le centre de rotation situé sur un des sommets de la
figure.Un triangle rectangle est prolongé sur la droite, mais le deuxième est à l’envers.La rotation avec le
centre de rotation situé sur le contour de la figure.Un rectangle est composé de deux triangles
rectangles.
Image
Un
exemple de translation, avec un triangle rectangle qui un effectué un glissement vers la droite.Un exemple de
réflexion, avec un triangle rectangle qui est devenu un triangle isocèle aigu.La réflexion, avec l’axe de
réflexion situé sur un côté de la figure.La rotation, avec le centre de rotation situé sur un des sommets de la
figure.Un triangle rectangle est prolongé sur la droite, mais le deuxième est à l’envers.La rotation avec le
centre de rotation situé sur le contour de la figure.Un rectangle est composé de deux triangles
rectangles.
Présenter la situation d’apprentissage dans un contexte intéressant en misant sur l’exploration et la découverte.
Par exemple, dire aux élèves : « Pour animer la construction d’un dallage à l’aide de l’ordinateur, il est important de déterminer à l’avance la transformation qu’on va utiliser pour déplacer une figure de la position A à la position B. Je vous propose donc d’entrer dans ce merveilleux monde de l’animation par ordinateur en explorant deux situations d’utilisation de transformations pour créer un dallage (voir l’annexe 6.2, explorations 1 et 2). Cette activité vous permettra également de découvrir une propriété importante des triangles (voir l’annexe 6.2, exploration 3). »
Pendant l’apprentissage (exploration)
Durée : environ 60 minutes
Former des équipes de deux élèves. Remettre à chacune une paire de triangles, soit les triangles A et B, C et D, E et F ou G et H (annexe 6.1) et leur demander de les découper. S’assurer que chacune des quatre paires de triangles est remise à au moins une équipe. Remettre aussi à chaque équipe plusieurs petites feuilles, une grande feuille et une copie de l’annexe 6.2 (Dalles-tu?).
Lire avec les élèves la démarche proposée à l’annexe 6.2 et s’assurer qu’elles et ils la comprennent. Expliquer que pour chacune des explorations, elles et ils doivent, tout comme les mathématiciennes et les mathématiciens, faire des observations, émettre des hypothèses, les vérifier et formuler des conclusions. Elles et ils doivent, entre autres, déterminer si chacune des situations mathématiques qui leur sont présentées est toujours vraie (c’est le cas des explorations 2 et 3), jamais vraie (c’est le cas de la première partie de l’exploration 1) ou parfois vraie (c’est le cas de l’activité « Tourne, tourne! »). Les énoncés à l’intérieur de chacune des explorations ont pour but de les guider dans leur travail.
Circuler parmi les élèves et intervenir, au besoin, afin de faire cheminer les élèves dans leurs réflexions. Porter une attention particulière aux hypothèses et aux conclusions qui sont formulées afin de choisir de façon stratégique les équipes qui seront invitées à faire une présentation au moment de l’échange mathématique. Voir l’annexe 6.3 pour un résumé des principales conclusions relatives à chacune des explorations.
|
Observations possibles |
Interventions possibles |
|
Des élèves croient qu’il est possible de créer un dallage en utilisant seulement la translation. |
|
|
Des élèves confondent la rotation dont le centre est situé sur un des sommets du triangle et la rotation dont le centre est situé sur le point milieu de l’un des côtés du triangle. |
|
|
Des élèves n’ont pas les angles 1, 2 et 3 à un point de rencontre de trois triangles. |
|
|
Des élèves laissent des espaces entre les triangles. |
|
Une fois la tâche terminée, allouer suffisamment de temps aux élèves pour qu’elles et ils se préparent à l’échange mathématique. Préciser qu’elles et ils doivent fournir des arguments mathématiques clairs, justes et convaincants pour justifier leurs conclusions.
Après l’apprentissage (objectivation/échange mathématique)
Durée : environ 25 minutes
Inviter les équipes choisies à venir à tour de rôle présenter leurs hypothèses et leurs conclusions. Encourager l’emploi d’un vocabulaire précis et de termes de causalité dans la communication. Voici des exemples de conclusions :
- Il est impossible de faire un dallage en utilisant seulement la translation parce qu’on ne remplit pas tous les espaces.
- Puisqu’on trouve les angles 1, 2 et 3 à un point de rencontre de trois triangles et qu’ils forment une ligne droite comme un angle plat, alors la somme des mesures des angles d’un triangle est égale à 180°, la mesure d’un angle plat.
Après chaque présentation, inciter les autres élèves à réagir et à poser des questions. Au besoin, poser des questions telles que :
- Qui peut expliquer dans ses mots la conclusion qu’on vient de présenter?
- Est-ce que d’autres élèves arrivent à la même conclusion?
- D’après ce qu’on vient de présenter, est-ce qu’on peut tirer une conclusion?
- Est-ce que cette conclusion est vraie pour tous les triangles?
Note : L’élaboration par les élèves de conclusions relatives à la possibilité ou à l’impossibilité de créer des dallages dans cette situation d’apprentissage reflète un cheminement vers le niveau de déduction informelle de la pensée géométrique. Les élèves ne peuvent pas encore prouver la validité de ces conclusions, mais elles et ils peuvent la déduire de façon informelle à partir des résultats obtenus dans un nombre limité de cas.
Différenciation pédagogique
|
Pour faciliter la tâche |
Pour enrichir la tâche |
Note : Il est plus facile de créer un dallage avec ces triangles parce que le triangle C est un triangle équilatéral et que le triangle D est un triangle isocèle rectangle.
Note : En indiquant le point milieu sur chacun des côtés, les élèves auront plus de facilité à effectuer la rotation à partir du centre de rotation qui se situe sur un de ces points. |
Note : C’est parfois possible, par exemple avec le triangle E.
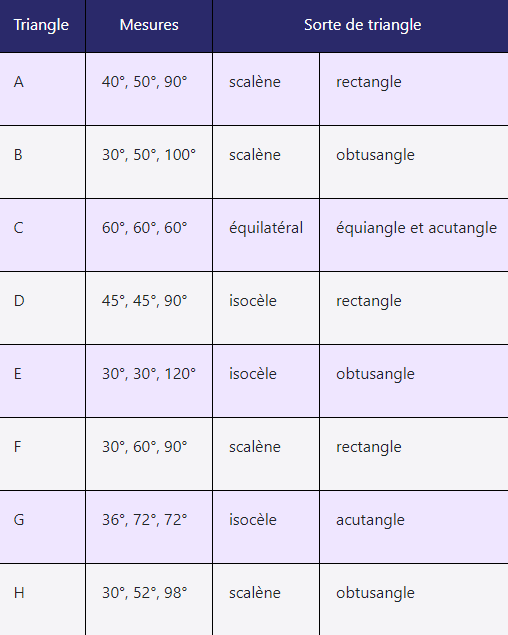 Image Un tableau, le triangle, les mesures, LA sorte de
triangle.Triangle « A » 40
degrés, 50 degrés, 90 degrés, triangle scalène rectangle.Triangle « B », 30 degrés, 50 degrés,
100 degrés, triangle scalène obtusangle.Triangle « C », 60 degrés, 60 degrés, 60 degrés,
triangle équilatéral, équiangle et acutangle.Triangle « D ». 45 degrés, 45 degrés, 90 degrés,
triangle isocèle rectangle.Triangle « E », 30 degrés, 30 degrés, 120 degrés, triangle isocèle,
obtusangle.Triangle « F », 30 degrés, 60 degrés, 90 degrés, triangle scalène, acutangle.Triangle
« G », 36 degrés, 72 degrés, 72 degrés, triangle isocèle, acutangle.Triangle «H » 30 degrés, 52
degrés, 98 degrés, triangle scalène, obtusangle. Image Un tableau, le triangle, les mesures, LA sorte de
triangle.Triangle « A » 40
degrés, 50 degrés, 90 degrés, triangle scalène rectangle.Triangle « B », 30 degrés, 50 degrés,
100 degrés, triangle scalène obtusangle.Triangle « C », 60 degrés, 60 degrés, 60 degrés,
triangle équilatéral, équiangle et acutangle.Triangle « D ». 45 degrés, 45 degrés, 90 degrés,
triangle isocèle rectangle.Triangle « E », 30 degrés, 30 degrés, 120 degrés, triangle isocèle,
obtusangle.Triangle « F », 30 degrés, 60 degrés, 90 degrés, triangle scalène, acutangle.Triangle
« G », 36 degrés, 72 degrés, 72 degrés, triangle isocèle, acutangle.Triangle «H » 30 degrés, 52
degrés, 98 degrés, triangle scalène, obtusangle. |
Suivi à la maison
Place au changement
À la maison, les élèves cherchent un dallage (par exemple, recouvrement d’un sol, d’un mur). En s’inspirant de l’activité effectuée en classe, les élèves créent et colorient un dallage qu’elles et ils aimeraient voir à la place du dallage existant.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 83-89.
Activité : et les quadrilatères, eux?
Mettre les élèves au défi de découvrir la propriété de la somme des mesures des angles intérieurs d’un quadrilatère.
Au besoin, leur suggérer de s’inspirer de la démarche utilisée dans la situation d’apprentissage Dalles-tu? et de
créer un dallage à partir d’un quadrilatère de leur choix en utilisant seulement des rotations en partant d’un
centre de rotation situé sur le point milieu de l’un des côtés du quadrilatère.
Note : Les élèves doivent d’abord identifier les quatre angles intérieurs du quadrilatère initial, par exemple à
l’aide des chiffres 1, 2, 3 et 4, et ensuite faire de même avec les angles intérieurs de tous les autres
quadrilatères du dallage. Elles et ils pourront alors constater qu’à chaque point de rencontre de quatre
quadrilatères, on trouve un angle plein formé par les quatre angles intérieurs du quadrilatère (angles 1, 2, 3 et
4). Puisqu’un angle plein mesure 360°, les élèves peuvent conclure que la somme des mesures des angles intérieurs
d’un quadrilatère est égale à 360°.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 90.
