B1.8 Utiliser des schémas pour comparer et ordonner des fractions unitaires désignant les portions individuelles obtenues lorsqu’un tout est divisé par des nombres différents de personnes, jusqu’à un maximum de 10.
Activité 1 : du plus petit au plus grand (lien entre le tout et les parties)
Démarche
Remettre une liste aléatoire de fractions simples, comme \(\frac{1}{2}\), \(\frac{1}{4}\) et \(\frac{1}{3}\).
Demander aux élèves de les mettre en ordre croissant en utilisant du matériel de manipulation.
Leur demander d’expliquer leur séquence et de la justifier.
Note : Représenter ces fractions avec du matériel concret à l’aide de divers modèles (surface, ensemble et longueur). Consulter le contenu d’apprentissage B1.7 pour obtenir plus d’informations sur ces modèles. Il est important que les élèves sachent ce que représente chaque fraction en fonction des modèles et qu’elles et ils soient capables de déterminer la fraction qui est la plus grande.
Circuler parmi les élèves et leur poser des questions telles que :
- Quelle fraction est la plus grande? la plus petite? Comment le sais-tu?
- Que représente chaque nombre dans une fraction?
- Qu’est-ce qui est différent entre les objets que tu as utilisés pour illustrer tes fractions et ceux des autres? Qu’est-ce qui est semblable?
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 68-69.
Activité 2 : comparaison des fractions unitaires
Trois amis reçoivent des cartes pour jouer au magasin. Ils ont 10 cartes en tout. Julien a un cinquième des cartes, tandis que Sophie a un demi des cartes. Quant à Loïsha, elle a un dixième des cartes. En comparant les fractions, combien de cartes reçoit chaque ami? Que remarques-tu?
Stratégie
Utiliser un modèle d’ensemble pour comparer des fractions unitaires
Je vais utiliser des cubes pour représenter le tout de 10 cartes.
Julien a un cinquième des cartes. Je prends 10 cubes et je forme 5 groupes. Le tout est divisé en cinquièmes, et chaque partie est un cinquième du tout. Un cinquième est une fraction unitaire. Dans cet ensemble, un cinquième est représenté par les 2 cubes verts. Alors, Julien a 2 cartes.
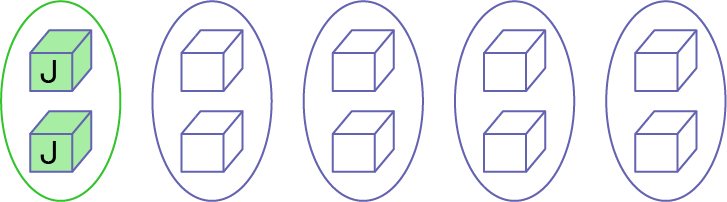
Sophie a reçu un demi des cartes. Je prends les mêmes 10 cubes et je forme 2 groupes. Le tout est divisé en demis, et chaque partie est un demi du tout. Un demi est une fraction unitaire. Dans cet ensemble, un demi est représenté par les 5 cubes bleus. Alors, Sophie a 5 cartes.
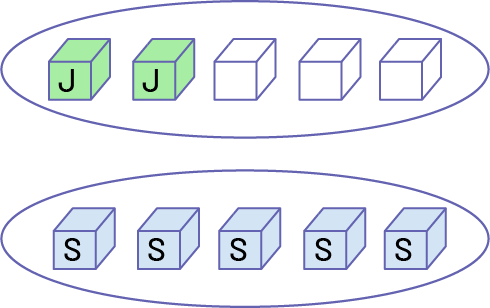image Deux ensembles de cinq cubes encerclés sont placés l’un au-dessus de l’autre. Dans le premier ensemble, deux cubes sur cinq sont verts et portent la lettre « J », tandis que les autres cubes sont blancs. Dans le deuxième ensemble, les cinq cubes sont bleus et portent la lettre « S ».
Loïsha a reçu un dixième des cartes. Je prends les 10 cubes et je forme 10 groupes. Le tout est divisé en dixièmes, et chaque partie est un dixième du tout. Un dixième est une fraction unitaire. Dans cet ensemble, un dixième est représenté par le cube jaune. Alors, Loïsha a une carte.
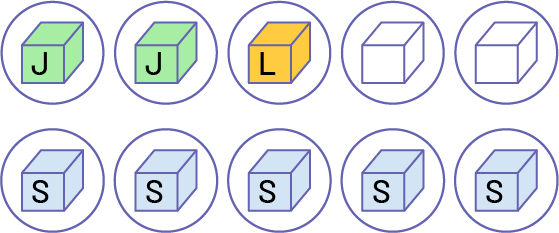image Deux rangées de cinq cubes sont placées l’une au-dessus de l’autre. Chaque cube est individuellement encerclé. Dans la première rangée, on trouve deux cubes verts portant la lettre « J », un cube jaune portant la lettre « L », et deux cubes blancs sans lettre. Dans la deuxième rangée, tous les cubes sont bleus et portent la lettre « S ».
Lorsque je compare les fractions unitaires un cinquième, un dixième et un demi, je remarque, dans cet ensemble de 10 cartes, qu’un dixième représente une carte seulement, qu’un cinquième représente 2 cartes et qu’un demi représente 5 cartes.
Alors, Sophie a 5 cartes, Julien a 2 cartes et Loïsha a 1 carte pour jouer au magasin.
Je remarque que, si le tout est divisé en de nombreuses parties, ses parties sont plus petites, et que si le tout est divisé en moins de parties, ses parties sont plus grandes.
Source : En avant, les maths! CM, Nombres, p. 3-4.