B2.4 utiliser des objets, des schémas et des équations pour représenter, décrire et résoudre des situations relatives à l’addition de nombres naturels dont la somme est égale ou inférieure à 50 et à la soustraction de nombres égaux ou inférieurs à 50.
Activité 1 : problèmes d’addition et de soustraction
Matériel
- sacs en plastique réutilisables (un par élève)
- bâtonnets de bois (cinq par élève)
- marqueurs
- gommettes
Remettre un sac en plastique et cinq bâtonnets de bois à chaque élève.
Leur demander de décorer les bâtonnets à l’aide des marqueurs ou des gommettes de façon à représenter cinq personnages.
Proposer aux élèves d’utiliser leurs personnages pour simuler les problèmes qui leur seront soumis.
Substituer les noms dans les problèmes énoncés par des noms des élèves de la classe.
Exemple de problème
Jacques, Julie et Corinne ont soif et vont boire à la fontaine. Combien y a-t-il de personnes à la fontaine? Renée et Jamal décident aussi d’aller boire. Combien de personnes se trouvent maintenant à la fontaine?
Écrire la phrase mathématique correspondante au tableau (\(\ 3 + 2 = 5\)).
Proposer d’autres problèmes du même genre, y compris des problèmes de soustraction.
Inviter les élèves à simuler l’histoire en allant se placer en ligne près du coin de lecture ou de mathématiques par exemple, ou à illustrer le problème à l’aide des personnages créés.
Former des équipes de deux et leur demander de composer des problèmes d’addition ou de soustraction mettant en scène les personnages créés.
Les inviter à présenter leurs problèmes au groupe-classe.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 98.
Activité 2 : problèmes sous forme d’énoncés
Matériel
- annexe 1SO.3 (Fiches de problèmes)
- petits objets (par exemple, jetons, cubes, boutons, attaches de sacs à pain)
Former de petites équipes pour que les élèves puissent faire la mise en scène d’un problème par équipe.
Mettre à la disposition des élèves des petits objets pour qu’elles et ils représentent les problèmes avec du matériel.
Choisir un problème dans l’annexe 1SO.3 (Fiches de problèmes) et le lire à la classe ou en projeter une copie et le lire avec les élèves.
Demander à une équipe de préparer la mise en scène du problème pendant que les autres se servent du matériel de manipulation pour illustrer la solution.
Inviter l’équipe à présenter le problème et poser des questions pour clarifier un point ou vérifier si les élèves qui les regardent ont compris.
Demander à quelques élèves d’expliquer la façon dont elles et ils ont résolu le problème à l’aide du matériel.
Faire écrire une phrase mathématique qui représente les termes et la somme.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 98-99.
Activité 3 : le réfrigérateur
Matériel
- annexe 1SO.4 (Modèle de réfrigérateur) (une copie par élève)
- bâtonnets de colle (un par élève)
- cahiers publicitaires d’épicerie en français
Remettre une copie de l’annexe 1SO.4 (Modèle de réfrigérateur) à chaque élève.
Guider les élèves dans la démarche qui suit pour préparer le réfrigérateur ou demander à des bénévoles de le faire avant le début de l’activité :
- Découper le contour du réfrigérateur.
- Découper la ligne continue séparant le réfrigérateur du congélateur jusqu’à la ligne pointillée.
- Appliquer de la colle au verso de la partie étroite du réfrigérateur (entre la ligne pointillée et le contour) et la coller sur un morceau de papier de bricolage.
- Tracer le contour du réfrigérateur sur le papier de bricolage et tirer une ligne pour séparer le réfrigérateur du congélateur.
- Replier les portes le long de la ligne pointillée pour pouvoir les ouvrir.
Découper de petites illustrations d’aliments dans des cahiers publicitaires d’épicerie.
Utiliser le réfrigérateur pour illustrer les concepts de décomposition et de regroupement dans l’addition.
Proposer un nombre à écrire sur l’aimant du réfrigérateur dessiné sur la porte (par exemple, 8).
Demander aux élèves de placer des illustrations d’aliments derrière les portes du réfrigérateur (par exemple, 5 illustrations) et du congélateur (par exemple, 3 illustrations) de manière à représenter le nombre (8) inscrit sur la porte.
Écrire une phrase mathématique qui représente les termes et la somme.
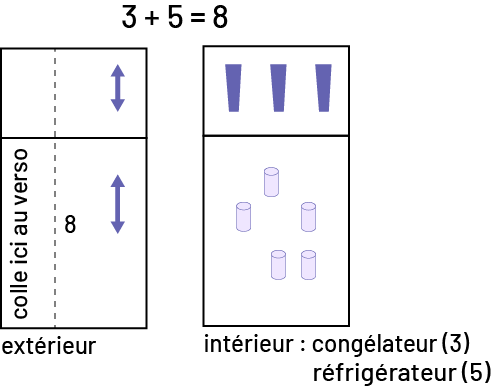image Deux rectangles placés côte à côte illustrent un réfrigérateur classique pourvu d’un congélateur en haut. Le rectangle de gauche représente l’extérieur et celui de droite représente l’intérieur. Au-dessus des rectangles est écrite l’équation suivante : trois plus cinq égale huit. Le premier rectangle présente deux doubles flèches pointant en haut et en bas, une sur le congélateur et une sur le réfrigérateur. Il y a une ligne pointillée qui le traverse de haut en bas. Du côté gauche de celle-ci, dans la section réfrigérateur, il est écrit « colle ici au verso ». Et à droite de celle-ci, sur la section réfrigérateur, il y a le nombre huit. Sous le rectangle, il est écrit le mot « extérieur ».Le deuxième rectangle présente trois verres de couleur violette dans le congélateur, et cinq cylindres violet pâle dans le réfrigérateur. Sous le rectangle, il est écrit : « intérieur : congélateur trois, réfrigérateur cinq ».
Assembler les illustrations des élèves afin de représenter toutes les répartitions du nombre et créer le livre « 8 ».
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 99-100.
Activité 4 : la voiturette de hot-dogs
Matériel
- annexe 1SO.5 (Plateau de jeu – Voiturette de hot-dogs) (une copie par élève)
- annexe 1SO.6 (Roulette “plus/moins”) (une roulette par équipe de deux)
- petits objets (environ 40 par élève)
- dés (un par équipe de deux)
Préparer des roulettes « plus/moins » à l’aide de l’annexe 1SO.6.
Former des équipes de deux et remettre un dé et une roulette « plus/moins » à chaque équipe.
Remettre à chaque élève une copie de l’annexe 1SO.5 (Plateau de jeu – Voiturette de hot-dogs) et une quarantaine d’objets.
Donner les directives suivantes :
- Placer 15 objets sur le plateau de jeu de façon à représenter des gens qui sont dans la file d’attente pour acheter des hot-dogs.
- Faire tourner la roulette « plus/moins » pour déterminer l’opération à effectuer.
- Lancer le dé pour savoir le nombre de personnes qui s’ajoutent à la file ou la quittent.
- Effectuer l’opération en déplaçant les objets.
- Jouer à tour de rôle jusqu’à ce que l’une des deux files disparaisse (parce qu’il n’y a plus personne) ou atteigne 30 personnes ou plus.
Enrichir la tâche en demandant aux élèves de composer un problème d’addition ou de soustraction à partir de la voiturette de hot-dogs. Elles et ils peuvent illustrer leur problème sur le plateau de jeu.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 100.
Activité 5 : à l’eau les nombres!
Matériel
- cartes numérotées de 1 à 12
- illustration d’un lac
- dés géants (trois)
Démarche
- Afficher les nombres de 1 à 12 au tableau ou sur un chevalet.
- Placer une illustration d’un lac sous les nombres.
- Le but du jeu est de mettre tous les nombres à l’eau en ordre de 1 à 12.
- Lancer les 3 dés géants et demander aux élèves de trouver une façon (soit en additionnant les chiffres, soit les en soustrayant) d’obtenir le nombre qui doit tomber à l’eau.
Les élèves peuvent utiliser deux nombres ou les trois nombres obtenus. Par exemple, le nombre ciblé est 5. Les nombres sont 3, 6 et 2. Les élèves peuvent dire \(\ 6 + 2 = 8\), ensuite \(\ 8 - 3 = 5\) ou simplement \(\ 3 + 2 = 5\).
Écrire les différentes réponses des élèves au tableau.
Si le nombre ciblé est impossible à trouver, lancer les dés de nouveau. Le jeu se termine lorsque tous les nombres de 1 à 12 sont à l’eau.
Questions à poser
Avant de lancer les dés, demander aux élèves : quels nombres aimerais-tu obtenir? Pourquoi?
Source : L’@telier - Ressources pédagogiques en ligne (atelier.on.ca).
Activité 6 : addition de nombres naturels
Exemple 1
Pendant la récréation, madame Picard voit 7 enfants sur la grande structure de jeu et 29 enfants qui jouent au ballon. Combien d’enfants voit-elle en tout?
STRATÉGIE
Addition à l’aide du point d’ancrage 10 et de la compensation
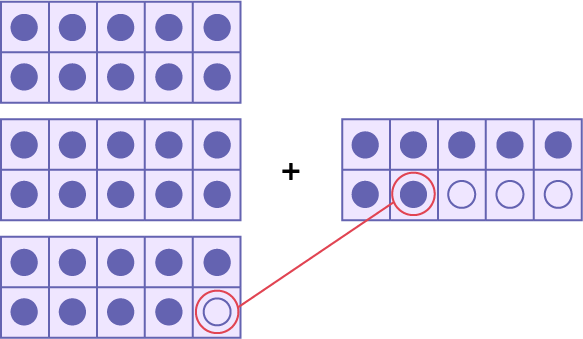image Quatre rectangles divisés en dix cases chacune munie d’une pastille sont présentés.En haut, il y a un rectangle muni de dix pastilles violettes.Au centre, il y a un rectangle muni de dix pastilles violettes, le symbole « plus », et un autre rectangle, celui-ci muni de sept pastilles violettes et de trois pastilles incolores. La dernière pastille violette est encerclée.En bas, il y a un rectangle muni de neuf pastilles violettes et d’une pastille incolore. Cette dernière est encerclée et reliée par un trait à la pastille encerclée du rectangle précédant.
Je représente 29 et 7 à l’aide de cadres à dix cases. Le nombre 29 est près de 30, donc j’enlève 1 au cadre avec 7 jetons, il en reste 6. Je l’ajoute à 29, ce qui me donne une autre dizaine, donc cela fait 30. Je dois maintenant faire l’addition de 30 et 6.
\(\ 30 + 6 = 36\)
Exemple 2
Dans un jardin, il y a 47 fleurs dont 33 sont des tulipes. Les autres sont des daphnés. Combien de daphnés sont dans le jardin?
STRATÉGIE
Addition à l’aide de la composition
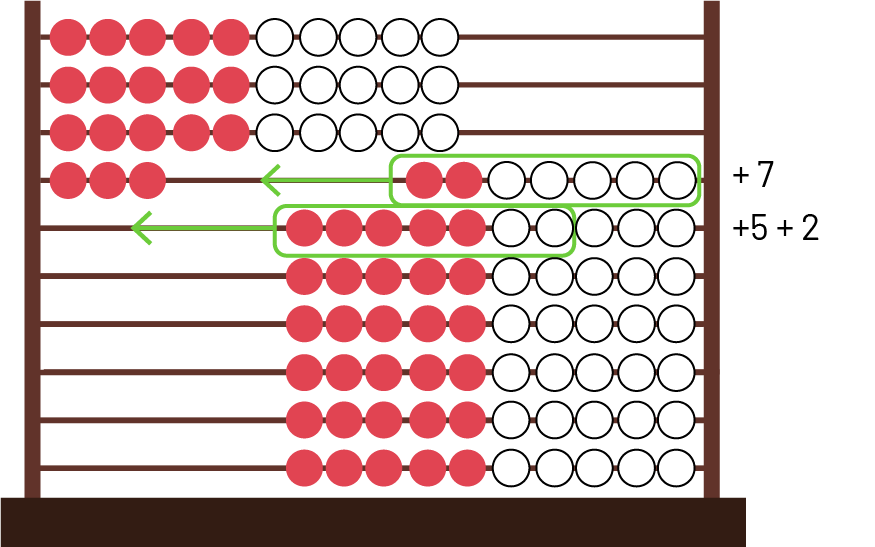image Voici l’illustration d’un Rekenrek muni de dix tiges, chacune munies de cinq perles rouges et cinq perles blanches.Sur les trois premières tiges, les cinq perles rouges et les cinq perles blanches sont entassées du côté gauche.Sur la quatrième tige, il y a trois perles rouges à gauche, ainsi que deux perles rouges et cinq perles blanches à droite. Les perles de droite sont encerclées en vert et une flèche pointe vers la gauche. À droite du Rekenrek, auprès de la quatrième tige, il est écrit « plus sept ».Sur la cinquième tige, toutes les perles sont à droite. Les cinq perles rouges et les deux premières perles blanches sont encerclées en vert et une flèche pointe vers la gauche. À droite du Rekenrek, auprès de la cinquième tige, il est écrit « plus cinq plus deux ». Sur toutes les tiges suivantes, toutes les perles sont entassées à droite.
À l’aide du Rekenrek, je représente les 33 tulipes par 3 rangées de 10 perles et 3 perles rouges sur la 4e rangée. Je dois ajouter les perles représentant les daphnés pour représenter 47 fleurs.
J’ajoute les 7 perles de la 4e rangée pour me rendre à 40. J’ajoute ensuite les 5 perles rouges et 2 des perles blanches de la 5e rangée pour me rendre à 47.
Par la suite, j’additionne tous ces ajouts.
\(\displaylines{\begin{align} 7 + 5 + 2 &= \\ 7 + 7 &= 14 \end{align}}\)
Donc, il y a 14 daphnés dans le jardin.
Source : En avant, les maths! 1re, CM, Nombres, p. 3-4.
Activité 7 : soustraction de nombres naturels
Exemple 1
Tout le long de l’année dans la classe d’éducation artistique, Anne a créé 39 œuvres d’art. Elle a donné certaines de ses œuvres à divers membres de sa famille. Il lui en reste 22. Combien d’œuvres d’art a-t-elle données à sa famille?
STRATÉGIE : Additionner pour soustraire à l’aide d’une grille de 50
Sur la grille de 50, j’encercle le nombre 39, ce qui représente le nombre d’œuvres d’art qu’Anne a au départ. J’encadre le nombre 22, ce qui représente le nombre d’œuvres d’art qu’il lui reste. À partir de 22, je fais un bond de 10, ce qui donne 32, un bond de 5, ce qui donne 37, et un bond de 2, ce qui donne 39.
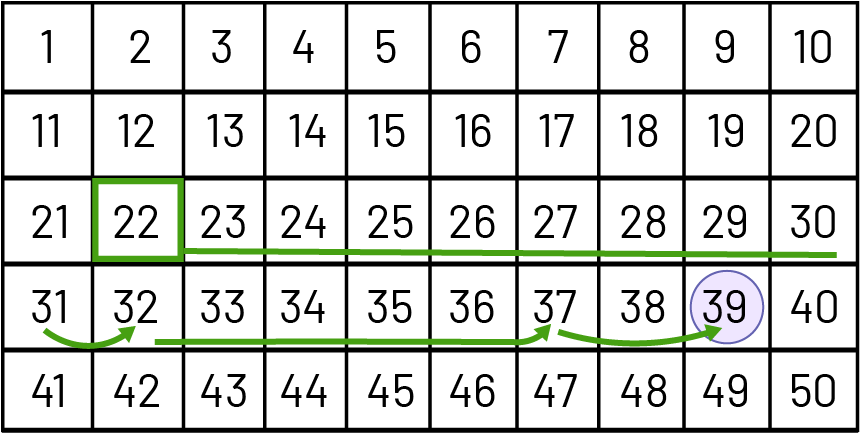
\(\displaylines{\begin{align}22 + \mathord{?} &= 39 \\ 22 + 10 + 5 + 2 &= 39 \\ 22 + 17 &= 39\end{align}}\)
Anne a donc donné 17 œuvres à sa famille.
Exemple 2
Luc a lu 36 pages dans son livre, tandis que Mélissa a lu 12 pages de moins du même livre. Combien de pages Mélissa a-t-elle lues?
STRATÉGIE : Effectuer une soustraction à l’aide de la valeur de position
J’utilise le matériel de base 10 pour représenter les 36 pages que Luc a lues. Je prends 3 bâtonnets pour représenter 3 dizaines et j’ajoute 6 petits cubes pour représenter 6 unités. De cette quantité, j’enlève 1 bâtonnet et 2 petits cubes pour représenter les 12 pages que Mélissa n’a pas lues. Il me reste alors 2 bâtonnets et 4 petits cubes, donc 2 dizaines et 4 unités. Mélissa a lu 24 pages (36 – 12 = 24).
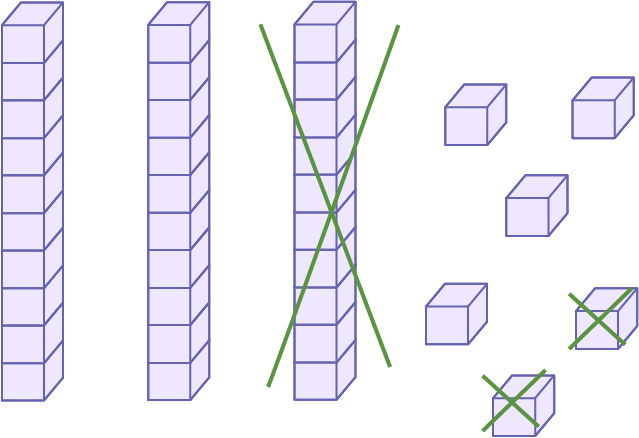
Source : En avant, les maths! 1re, CM, Nombres, p. 3-4.