B2.1 Utiliser les propriétés des opérations, et démontrer les relations entre la multiplication et la division pour résoudre des problèmes et vérifier la vraisemblance des calculs.
Activité 1 : je confectionne un collier (commutativité de l’addition)
Demander aux élèves de confectionner un collier en enfilant 5 perles rouges et 2 perles bleues, puis leur suggérer d’écrire la phrase mathématique correspondante.
\(5 + 2 = 7\)

Demander aux élèves de tourner le collier et d’écrire la phrase mathématique correspondante.
\(2 + 5 = 7\)

Proposer ensuite aux élèves de comparer les 2 phrases mathématiques et de répondre aux questions suivantes :
- Que remarquez-vous au sujet de l’ordre des perles?
- Que remarquez-vous au sujet de la quantité de perles?
- Pourquoi la quantité est-elle la même dans les 2 cas?
- Changez la quantité de perles sur le collier et écrivez 2 phrases mathématiques. Comparez les phrases mathématiques. Que remarquez-vous?
- Si vous faites la même démarche en utilisant une grande quantité de perles sur le collier comme 100, 300 ou 500, que pouvez-vous affirmer au sujet des quantités que vous observez?
Note : Refaire l’activité avec de plus grandes quantités. Refaire l’activité en demandant aux élèves de se déplacer pour observer le collier dans l’autre direction au lieu de le tourner.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 91.
Activité 2 : les wagons du train (associativité)
Présenter aux élèves 3 wagons de train construits avec des cubes emboîtables de différentes couleurs.

Leur proposer d’aider M. Bontrain, le chef de train qui désire regrouper 2 wagons sans en modifier l’ordre.
Représenter chaque situation possible à l’aide des cubes et écrire la phrase mathématique correspondante. Afin d’éviter d’avoir recours aux parenthèses, utiliser des encadrés pour illustrer les wagons.
Note : Les wagons peuvent être regroupés de 2 façons :
- regrouper les wagons 1 et 2;

- regrouper les wagons 2 et 3.

Poser les questions suivantes aux élèves :
- Y a-t-il d’autres regroupements possibles de wagons? Comment le savez-vous?
- Quelle est la somme des cubes qui forment le train dans chaque cas? (Les 2 sommes sont égales à 7; elles sont pareilles.)
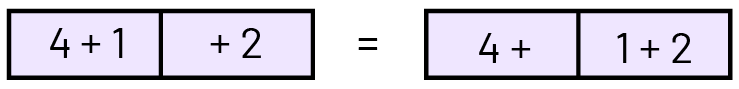
- Comment est-ce possible que la somme reste pareille même si nous avons différents regroupements de wagons? (Ce sont les mêmes cubes qui sont regroupés différemment; la quantité totale de cubes ne change pas.)
- Est-ce que cela fonctionnerait avec 3 autres nombres? Démontrez-le à l’aide d’une droite numérique ouverte double et d’une phrase mathématique.
Leur demander d’expliquer à un ou une autre élève ce qu’ils ont observé. Par la suite, leur demander :
- Que pourriez-vous écrire dans votre journal mathématique collectif au sujet de ce que vous avez découvert aujourd’hui?
Reprendre l’activité avec un plus grand nombre de wagons.
Note : Si les élèves connaissent la propriété de commutativité, certains pourraient modifier l’ordre des termes à additionner (par exemple, \(4 + 2 + 1\)). Si tel est le cas, leur demander de justifier pourquoi il est possible de modifier l’ordre. Sinon, mentionner simplement que l’ordre des wagons ne peut être modifié puisqu’ils sont attachés ainsi sur la voie ferrée.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 99-100.
Activité 3 : la disposition rectangulaire
Demander aux élèves de représenter \(5 \times 8\) et \( 8 \times 5\) à l’aide de dispositions rectangulaires.
Voici des représentations possibles :
 Image 4 dispositions rectangulaires : Représentation de 5 multiplié par 8. 5 colonnes de 8 jetons. Représentation de 8 multiplié par 5. 8 colonnes de 5 jetons. Représentation de 8 multiplié par 5. 8 rangées de 5 jetons. Représentation de 5 multiplié par 8. 5 rangées de 8 jetons.
Image 4 dispositions rectangulaires : Représentation de 5 multiplié par 8. 5 colonnes de 8 jetons. Représentation de 8 multiplié par 5. 8 colonnes de 5 jetons. Représentation de 8 multiplié par 5. 8 rangées de 5 jetons. Représentation de 5 multiplié par 8. 5 rangées de 8 jetons.
Procéder de la même façon avec diverses multiplications de 2 nombres.
Poser des questions pour faire comprendre la commutativité de la multiplication telles que :
- Que vois-tu?
- Combien y a-t-il de jetons? de rangées? de colonnes?
- Je tourne la disposition rectangulaire (90°). Combien y en a-t-il maintenant?
- Quel est le produit de 5 et 8? Quel autre fait de multiplication lui ressemble?
- En tournant les dispositions rectangulaires, quelles autres paires de nombres donnent le même produit?
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 42.
