B2.9 Utiliser les rapports de 1 à 2, de 1 à 5 et de 1 à 10 pour résoudre des problèmes, y compris des problèmes faisant appel au raisonnement proportionnel.
Activité 1 : des groupes partout!
Étape 1
Expliquer aux élèves que le monde qui les entoure est rempli de choses qui viennent en groupes, que ce soit à l’école, à la maison, dans la nature ou ailleurs autour d’eux.
Placer les élèves en groupes de 2 et remettre une feuille de papier que les élèves vont séparer en 3 colonnes.
Demander aux élèves de nommer des choses qui viennent en groupes de 2, 5 et 10 et de les inscrire dans leur tableau.
Exemples
| Groupes de 2 | Groupes de 5 | Groupes de 10 |
|---|---|---|
| Bas Mitaines Yeux Jambes Jumeaux Souliers Roues d’une bicyclette Oreilles Mains Pouces Bras Épaules |
Côtés d’un pentagone Quintuplés Orteils d’un pied Joueurs d’une équipe de basket-ball Doigts d’une main Jours d’école dans une semaine Cents dans un 5 cents |
Tentacules d’un calmar Doigts Orteils |
Étape 2
Remettre à chaque groupe environ 40 cubes emboîtables.
Choisir une suggestion de groupement recueillie sur la liste du groupe-classe (par exemple, mitaines [2]).
Demander aux élèves de résoudre le problème ci-dessous en utilisant des cubes emboîtables.
Il y a 5 paires de mitaines dans le bac. Combien de mitaines y a-t-il?
Demander aux élèves de représenter la relation de proportionnalité entre les 2 rapports à l’aide d’une illustration, d’une droite numérique double ou d’une table de valeurs.
Exemple
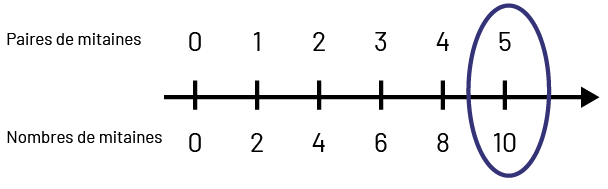Image Droite numérique qui représente les paires de mitaines sur sa partie supérieure et les nombres de mitaines dans
sa partie inférieure. Donc la droite est graduée de deux façons, au-dessus de la droite de zéro à 5 par intervalles réguliers de plus un.
La droite est graduée par en dessous de zéro à dix par intervalles réguliers de plus 2. La marque qui représente 5 et
dix est encerclé.
Donner aux élèves le temps requis pour résoudre le problème et discuter de leur solution avec leur partenaire.
Poursuivre cette activité avec les divers regroupements de 2, 5 et 10 en créant des problèmes (en tenant compte que les élèves ont environ 40 cubes emboîtables) et en demandant aux élèves de les résoudre.
Source : adapté Les mathématiques… un peu, beaucoup, à la folie!, Guide pédagogique, Édition révisée, Numération et sens du nombre, 3e année, Module 2, Série 1, Activité 1 - Des groupes tout autour de nous, p. 215 et 216.
Activité 2 : je mélange le jus
Pour la journée d’athlétisme, les élèves de la classe de Mme Guérin préparent du jus pour les coureurs. Pour chaque contenant de jus concentré, il faut ajouter 5 contenants d’eau. Combien leur faudra-t-il ajouter de contenants d’eau à 4 contenants de jus concentré?
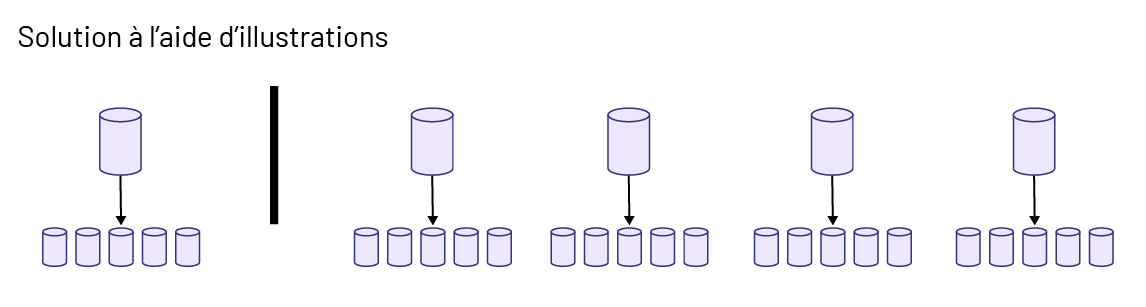
Il faudra donc 20 contenants d’eau.
Activité 3 : les cahiers
Présenter le problème suivant aux élèves et leur demander de le résoudre à l’aide de la stratégie de leur choix.
Les cahiers distribués dans les écoles sont vendus en paquets de 10 cahiers.
- Combien de cahiers y a-t-il dans 5 paquets? (50 cahiers)
- Si l’école a besoin de 100 cahiers, combien de paquets doit-elle commander? (10 paquets)