B2.2 Se rappeler les faits de multiplication de 1 × 1 à 10 × 10 et les faits de division associés, et démontrer sa compréhension de ces faits.
Habileté : démontrer sa compréhension des faits de multiplication et de division
L’apprentissage des faits numériques de base associés à la multiplication et à la division est incontournable. Comme leur nom l’indique, ils sont la base des opérations et un outil indispensable pour travailler avec de plus grands nombres. Il est important que les élèves apprennent à maîtriser les faits numériques de base.
Or, il existe des stratégies d’enseignement qui permettent aux élèves de les apprendre. Il n’est pas nécessaire d’apprendre les faits par cœur en les répétant et en utilisant des cartes-éclairs. Cette façon de faire, qui entraîne la mémorisation des faits en tant que connaissances distinctes, exige la mémorisation de près de 400 faits isolés. Elle sollicite beaucoup la mémoire, puisque l’apprentissage des faits n’est pas basé sur la création de liens.
L’apprentissage des faits numériques doit plutôt s’appuyer sur l’habileté des élèves à créer des liens et sur leurs connaissances antérieures. Le rôle du personnel scolaire est de présenter des stratégies et d’outiller les élèves. Par exemple, pour apprendre les faits de multiplication par 9, les élèves peuvent se servir de la stratégie « c’est un ensemble de moins que » : on multiplie le nombre par 10 et on soustrait un ensemble. Un élève pourrait donc tenir le raisonnement suivant : \(9\; \times \;8\), c’est comme \(10\; \times \;8\; = \;80\), moins un groupe de 8; c’est donc 72. Cette stratégie l’aide à répondre correctement et rapidement et à comprendre les quantités en jeu dans cette multiplication.
Avec la pratique, les élèves ont de moins en moins recours aux stratégies et développent des automatismes pour trouver plusieurs faits de base. Les élèves seront peut-être incapables d’énoncer spontanément toutes les réponses des faits numériques de base, mais pourront les trouver rapidement en ayant recours aux stratégies apprises, comme c’est le cas de plusieurs adultes qui ont un excellent sens du nombre.
Les faits sont appris jusqu’à \(9\; \times \;9\) et il n’est pas nécessaire d’apprendre les faits de multiplication jusqu’à 12. Si les élèves ont besoin de multiplier 8 par 12, elles et ils peuvent avoir recours à la table de 10 et la table de 2 (par exemple, \(12\; \times \;8\; = \;10\; \times \;8\; + \;2\; \times \;8\)) ou encore multiplier 8 par 6 et doubler la réponse.
La liste ci-après présente les stratégies et les propriétés les plus répandues pour l’apprentissage des faits numériques de base. En général, les élèves n’utilisent pas tous les mêmes stratégies. De plus, ils n’emploient pas toutes les stratégies existantes, mais en choisissent habituellement une ou plusieurs, selon leur habileté et les faits numériques traités.
Source : Guide d'enseignement efficace des mathématiques de la 4e à la 6e année, p. 88-89.
La multiplication peut être représentée sous forme d’addition répétée, de dispositions rectangulaires ou d’un ensemble de groupes égaux.
Voici quelques propriétés et stratégies qui favorisent la compréhension conceptuelle de la multiplication :
- la propriété de l’élément neutre dans la multiplication de nombres naturels (\(a\; \times \;1\) donne toujours a);
- la propriété du 0 dans la multiplication de nombres naturels (\(0\; \times \;a\) donne toujours 0);
- la propriété de commutativité \(\left( {2\; \times \;3\; = \;3 \times \;2} \right)\);
- la propriété de distributivité \(\left[ {5\; \times \;6\; = \;5\; \times \;\left( {4\; + \;2} \right)\; = \;\left( {5\; \times \;4} \right)\; + \;\left( {5\; \times \;2} \right)} \right]\) ;
- la propriété d’associativité \(\left[ {5\; \times \;12\; = \;5\; \times \;\left( {2\; \times \;6} \right)\; = \;\left( {5\; \times \;2} \right)\; \times \;6} \right]\) ;
- l’opération inverse de la division.
La division peut être représentée sous forme de soustractions répétées, d’une répartition égale ou de partage.
Voici quelques propriétés et stratégies qui favorisent la compréhension conceptuelle de la division :
- la propriété de l’élément neutre dans la division de nombres entiers (\(a\; \div \;1\) donne toujours a);
- le rapport entre la division et le sens de la fraction (12 bonbons divisés en 3 groupes représentent à la fois \(12\; \div \;3\) et le tout divisé en 3 parties);
- l’opération inverse de la multiplication.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 21-22.
Régularités dans des suites de nombres
Les élèves développent une meilleure compréhension du sens des opérations arithmétiques en explorant les régularités qu’elles génèrent dans les suites de nombres. Les élèves peuvent utiliser la droite numérique ou la grille de nombres pour analyser les suites de nombres obtenues lorsqu’on compte par intervalles. Par exemple, si on compte par intervalles de 10 à partir d’un chiffre quelconque de 0 à 9, tous les nombres obtenus se termineront par ce chiffre (par exemple, si on commence à compter à 3, on aura la suite 3, 13, 23, 33, 43…).
L’étude des régularités dans les suites de nombres facilite aussi l’apprentissage des faits numériques de base (par exemple, tous les multiples de 5, soit 5, 10, 15, 20, 25…, se terminent par 5 ou 0) et l’établissement de liens entre les nombres (par exemple, tous les multiples de 10 [▲] sont aussi des multiples de 5 [●]).
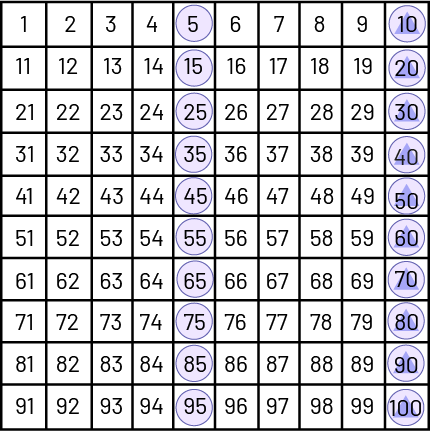 image Grille de nombres de, un à 100. Tous les multiples de 5 sont encerclés : 5, dix, 15, 20, 25,
30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100.Tous les multiples de dix sont marqués d’un triangle :
dix, 20, 30, 40, 50, 60, 70, 80, 90, 100.
image Grille de nombres de, un à 100. Tous les multiples de 5 sont encerclés : 5, dix, 15, 20, 25,
30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100.Tous les multiples de dix sont marqués d’un triangle :
dix, 20, 30, 40, 50, 60, 70, 80, 90, 100.
… ou encore, tous les multiples de 6 [▲] sont aussi des multiples de 3 [●]).
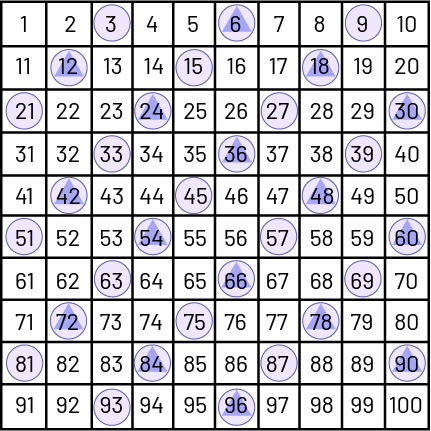 image Grille de nombres de, un à 100. Les multiples de 3 sont encerclés: 3, 6, 9, 12, 15, 18, 21, 24,
27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96.Les multiples de 6 ont
un triangle:6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96.
image Grille de nombres de, un à 100. Les multiples de 3 sont encerclés: 3, 6, 9, 12, 15, 18, 21, 24,
27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60, 63, 66, 69, 72, 75, 78, 81, 84, 87, 90, 93, 96.Les multiples de 6 ont
un triangle:6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96.
Les élèves prennent généralement plaisir à découvrir des régularités dans les suites de nombres générées par les opérations arithmétiques, chaque découverte suscitant habituellement un sentiment d’émerveillement. Les activités liées à la recherche de régularités encouragent les élèves à jongler avec les nombres et favorisent le développement de la pensée divergente et de l’esprit d’analyse, deux composantes importantes de la pensée mathématique. De plus, l’habileté à explorer les régularités est essentielle à l’étude de l’algèbre et de la géométrie.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 3e année, p. 30-31.
Apprendre les faits numériques de base relatifs à la multiplication et à la division
Pour apprendre les faits numériques de base relatifs à la multiplication et de la division, il ne suffit pas de les mémoriser. Il est important de comprendre que ces opérations peuvent être abordées de façons différentes.
Faits numériques de base relatifs à la multiplication
- Les faits numériques de base de multiplication sont tous les faits de multiplication de \(0\; \times \;0\) jusqu’à \(9\; \times \;9\).
- Il y a 100 faits de base de multiplication.
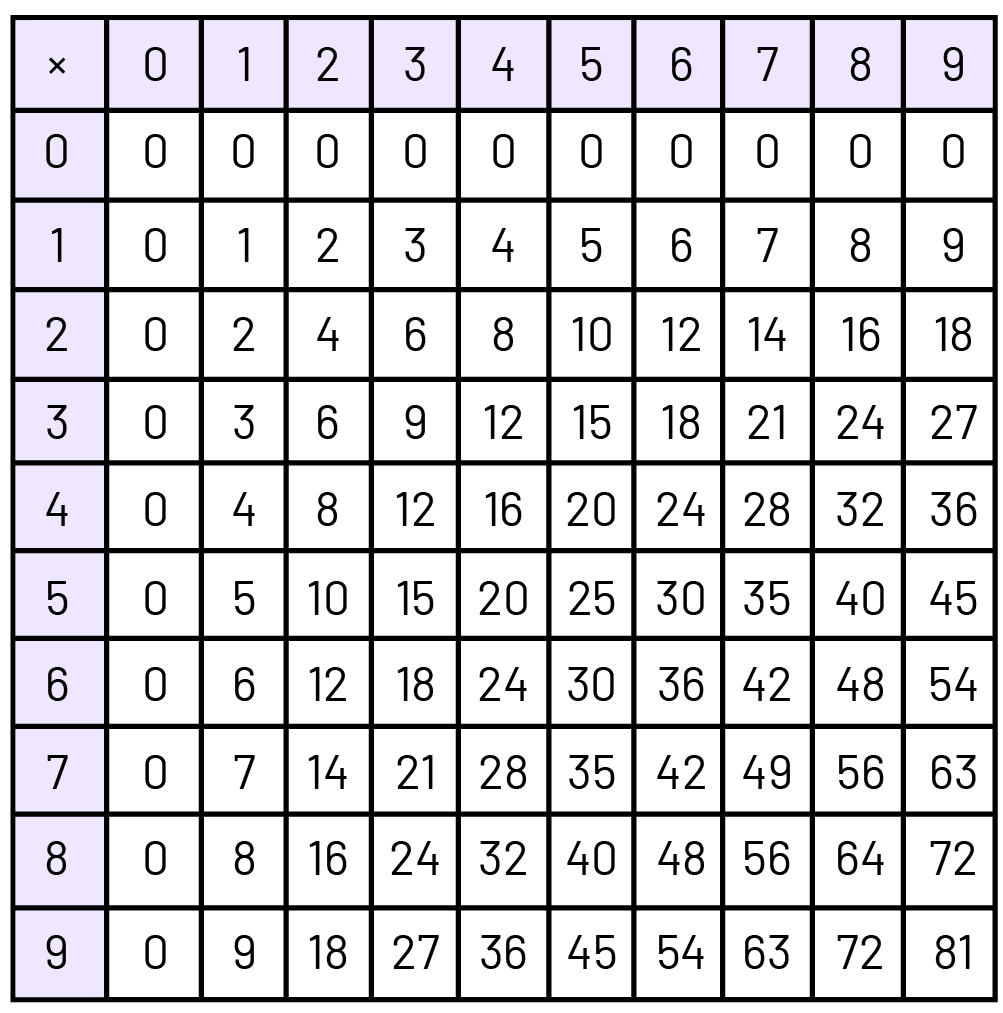
Faits numériques de base relatifs à la division
- La grille de multiplication peut aussi servir à la division.
- Les faits numériques de la division sont l’inverse des faits numériques de multiplication, depuis \(81\; \div \;9\) jusqu’à \(1\; \div \;1\).
- Il y a 90 faits de base pour la division.
- Il n’y a pas de faits comprenant 0 parce qu’il est impossible de se servir de 0 comme diviseur.
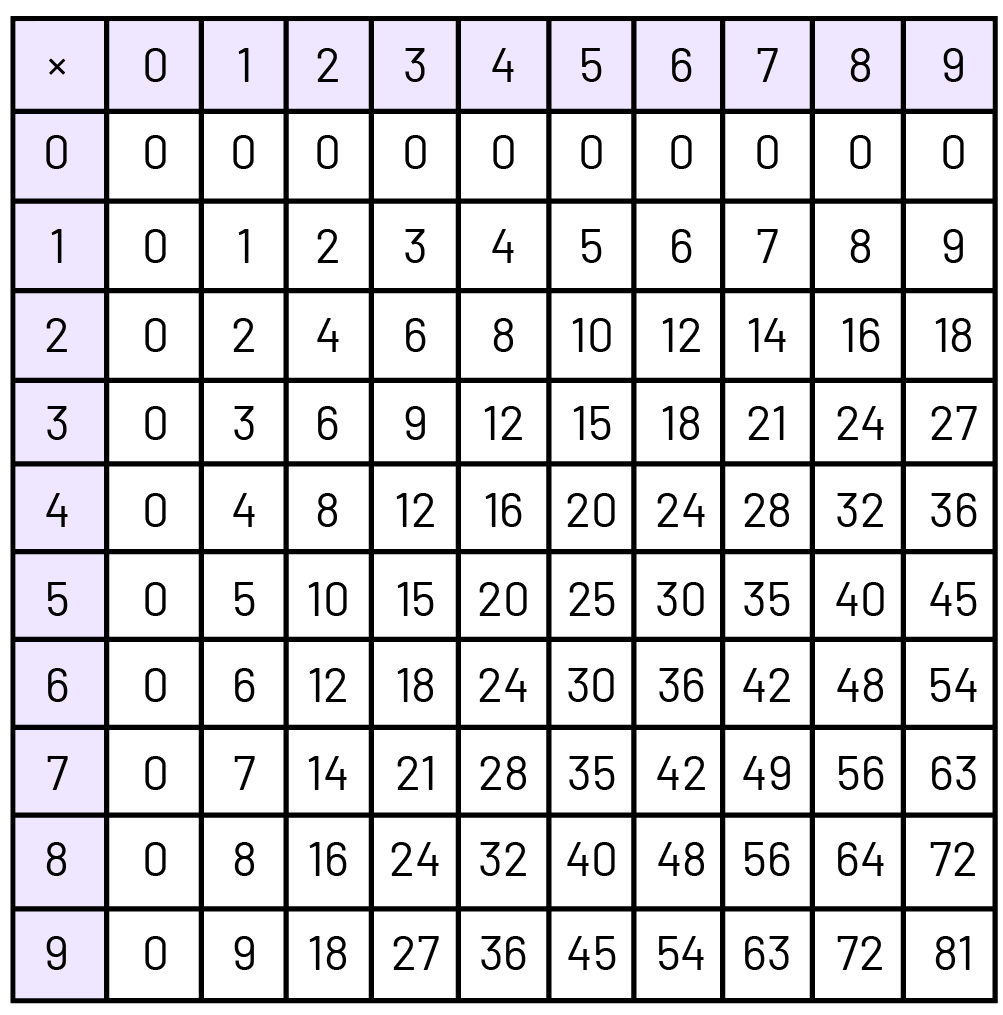
Modèles pour représenter des faits numériques de base relatifs à la multiplication et à la division
Plusieurs modèles peuvent être utilisés pour amener les élèves à comprendre la multiplication et la division. Ils permettent aux élèves :
- de saisir le sens des symboles dans les opérations et d’établir des liens entre les dessins/images, les mots et les symboles;
- de comprendre le sens des opérations et d’utiliser différentes représentations – concrètes, semi-concrètes et symboliques.
De nombreux modèles peuvent être élaborés à l’aide du matériel ci-dessous pour amener les élèves à comprendre la multiplication et la division :
- des objets concrets, comme des jetons, des bâtonnets et des carreaux, ainsi que divers contenants pour les y placer;
- des cubes emboîtables;
- du matériel visuel, comme des illustrations;
- des dispositions rectangulaires (arrangement de rangées et de colonnes);
- du matériel de base dix;
- des pièces de monnaie (1 ¢, 5 ¢, 10 ¢, 25 ¢ et 1 $);
- du papier quadrillé;
- des droites numériques;
- des grilles de nombres.
Les modèles de tous genres peuvent aider les élèves à établir des relations et ainsi à mieux comprendre ce que représentent les symboles dans les opérations. Les élèves ont besoin de travailler avec des représentations qui les aident à percevoir les relations entre la multiplication et les additions répétées, et entre la multiplication et la division (les élèves qui font l’apprentissage de la division longue peuvent également tirer parti des représentations qui les aident à percevoir les divisions longues comme des soustractions répétées ou des additions répétées). La compréhension des dispositions rectangulaires comme outil de multiplication ou de division se développe avec le temps et la pratique. Une fois que les élèves peuvent se représenter des faits tels que \(5\; \times \;6\) à l’aide de dispositions rectangulaires, elles et ils peuvent se servir de celles-ci pour trouver la réponse à \(50\; \times \;6\), et ainsi de suite.
Les représentations de tous genres aident les élèves à faire des rapprochements entre les modèles, les symboles et les mots. On trouvera ci-dessous différentes représentations du fait numérique de base \(2\; \times \;6\) . Chacune des 7 représentations est appropriée. Rappelons seulement que les élèves éprouvent moins le besoin de recourir aux représentations visuelles à mesure qu’elles et ils développent certains automatismes pour résoudre les faits numériques de base.
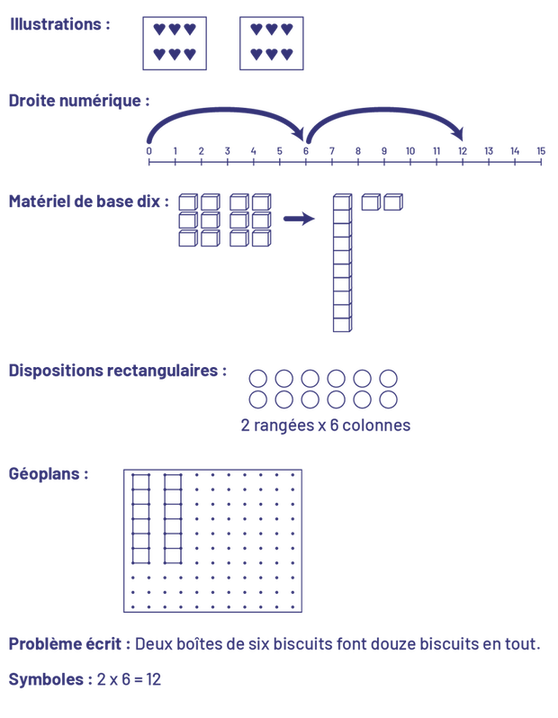 Image un:
Illustrations.2 rectangles contenant chacun 6 cœurs.Image 2: Droite numérique. Une droite numérique graduée de zéro à
15 par intervalles de, un. Une flèche part de zéro et pointe le 6 et une autre flèche part du 6 et pointe le 12.Image
3: Matériel base de dix2 ensembles de 6 cubes suivis d’une flèche pointant vers une réglette de dix cubes et 2 cubes à
part.Image 4: Dispositions rectangulaires.2 rangées fois 6 colonnes.2 lignes de 6 petits cercles.Image 5: GéoplansOn y
voit un géoplan sur lequel 2 rectangles de 6 unités chacun sont surlignés.Image 6: Problème écrit: 2 boîtes de 6
biscuits font douze biscuits en tout.Symbole: 2 fois 6 égal 12.
Image un:
Illustrations.2 rectangles contenant chacun 6 cœurs.Image 2: Droite numérique. Une droite numérique graduée de zéro à
15 par intervalles de, un. Une flèche part de zéro et pointe le 6 et une autre flèche part du 6 et pointe le 12.Image
3: Matériel base de dix2 ensembles de 6 cubes suivis d’une flèche pointant vers une réglette de dix cubes et 2 cubes à
part.Image 4: Dispositions rectangulaires.2 rangées fois 6 colonnes.2 lignes de 6 petits cercles.Image 5: GéoplansOn y
voit un géoplan sur lequel 2 rectangles de 6 unités chacun sont surlignés.Image 6: Problème écrit: 2 boîtes de 6
biscuits font douze biscuits en tout.Symbole: 2 fois 6 égal 12.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 21-24.
Stratégies de rappel pour apprendre les faits numériques de multiplication et de division
Avant de pouvoir apprendre les faits numériques de la multiplication et de la division, les élèves doivent comprendre comment faire des groupes égaux et les compter, et comment répartir un tout en groupes égaux. Elles et ils doivent aussi savoir compter par intervalles de 2, 3, 4, 5 et 10. Les stratégies portant sur les faits numériques de base relatifs à la multiplication et à la division visent à aider les élèves à s’appuyer sur leurs connaissances et leurs expériences antérieures pour apprendre à utiliser ces nouvelles stratégies (répartition en groupes égaux, compter par intervalles…).
Les stratégies qui suivent ne sont pas présentées selon un ordre particulier. Il arrive que des élèves trouvent certaines stratégies plus utiles que d’autres ou ignorent certaines stratégies au profit de leurs propres stratégies. D’autres trouvent plus facile de mémoriser les faits que de s’appuyer sur une stratégie. Quel que soit le cas, l’objectif premier du personnel enseignant est d’amener tous les élèves à bien comprendre la multiplication et la division.
La commutativité
Les élèves bénéficient d’expériences qui les aident à reconnaître la propriété de commutativité de la multiplication (\(2\; \times \;4\; = \;4\; \times \;2\)). Les élèves qui comprennent la commutativité peuvent mettre à profit la moitié des faits numériques de base pour apprendre l’autre moitié.
Grille de commutativité
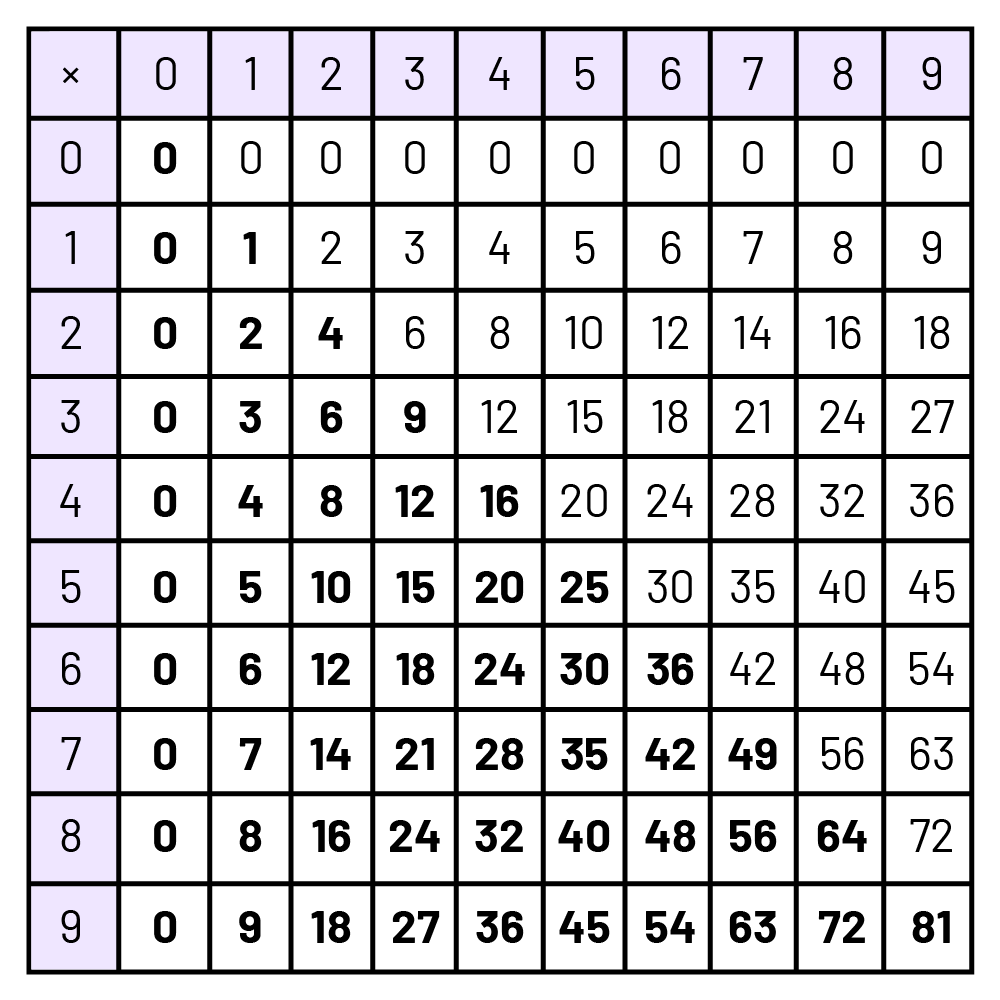
Les faits numériques avec 0 et 1
Les élèves bénéficient d’expériences qui les aident à comprendre le concept d’élément neutre – tout nombre multiplié ou divisé par 1 donne ce nombre comme résultat (par exemple, \(1\; \times \;3\; = \;3,\;6\; \div \;1\; = \;6\)) – et le concept d’élément absorbant de la multiplication — tout nombre multiplié par 0 donne 0 comme résultat (par exemple, \(100\; \times \;0\; = \;0\)). Pour faire comprendre ces concepts aux élèves, il est plus utile de leur poser des problèmes tels que « Si je te donne 3 paquets de 0 biscuit, combien de biscuits as-tu? » que de leur faire mémoriser.
Les doubles
La table de multiplication de 2 devrait être reliée aux connaissances que les élèves ont déjà acquises sur l’addition de doubles. Cette stratégie est particulièrement importante parce que les élèves qui maîtrisent bien la table de 2 peuvent relier ces faits numériques à la table de multiplication de 3. En effet, si \(2\; \times \;4\;\)donne 8, il s’ensuit que \(3\; \times \;4\;\)est égal à 8 plus un autre 4.
Le double et encore le double
Les élèves qui maîtrisent les faits relatifs aux doubles (la table de multiplication de 2) peuvent appliquer cette connaissance à la table de 4. Tout nombre fois 4 donne le même résultat que lorsqu’on multiplie ce nombre par 2 et que l’on double la réponse (par exemple, 4 x 6 donne le même résultat que \(2\; \times \;6\; = \;12\) que l’on double pour obtenir 24).
(Van de Walle et Folk, 2005, p. 152, traduction libre)
Le double et un ensemble de plus
De la même façon, les élèves qui maîtrisent les faits numériques relatifs aux doubles (la table de multiplication de 2) peuvent appliquer cette connaissance à la table de 3. En effet, si \(2\; \times \;4\;\)donne 8, il s’ensuit que \(3\; \times \;4\;\)est égal à 8 plus un autre 4, ce qui donne 12.
(Van de Walle et Folk, 2005, p. 152, traduction libre)
Les faits numériques relatifs à 5
Les élèves qui sont habitués à compter par 5 et à reconnaître les régularités de 5 dans une grille de nombres n’ont généralement pas de difficulté à apprendre les faits numériques de base relatifs à 5. Il existe toute une gamme de chansons, de comptines et de livres d’histoire portant sur le 5 dont on peut se servir pour appuyer l’apprentissage de cette stratégie.
Un ensemble de plus ou un ensemble de moins
Si l’élève sait que \(6\; \times \;7\; = \;42\), il lui est facile de calculer \(6\; \times \;8\) en ajoutant un autre 6 à 42 pour arriver à 48. Cette stratégie est particulièrement utile pour la table de 6 qui peut être assez difficile à apprendre pour certaines et certains élèves. Ceux qui maîtrisent bien la table de multiplication de 5 peuvent déterminer le produit d’un nombre multiplié par 6 en multipliant ce nombre par 5 (par exemple, \(5\; \times \;7\; = \;35\)) et en additionnant une fois ce facteur au produit trouvé (par exemple, \(35\; + \;7\; = \;42\), donc \(6\; \times \;7\; = \;42\)). (Van de Walle et Folk, 2005, p. 152, traduction libre). De même, si l’élève doit trouver le produit de \(8\; \times \;7\) et qu’il connaît \(8\; \times \;8\; = \;64\), il peut utiliser la même stratégie à rebours, c’est-à-dire soustraire un 8 de 64 pour obtenir 56.
La table de 9
La table de multiplication de 10 est généralement assez facile à apprendre parce que les élèves apprennent à compter par 10 dès leur plus jeune âge. Une fois la table de 10 bien maîtrisée, les élèves peuvent établir des liens avec la table de 9 en calculant le fait de multiplication par 10 correspondant et en soustrayant l’autre facteur une fois. Par exemple, si 10 x 8 donne 80, il s’ensuit que \(9\; \times \;8\) équivaut à 80 moins un 8, soit 72.
Le personnel enseignant peut aider les élèves à reconnaître certaines régularités dans la table de 9. Par exemple, tous les produits de la table de 9 sont composés de chiffres qui, additionnés ensemble, égalent 9 \(\left( {5\; \times \;9\; = \;45;\;\;\;4\; + \;5\; = \;9} \right)\). De plus, le chiffre des dizaines dans le produit est toujours 1 de moins que le facteur qui multiplie 9. Par exemple, dans \(6\; \times \;9\; = \;54\), le chiffre des dizaines est 1 de moins que le multiplicateur 6 (donc 5) et la somme des 2 chiffres du produit donne 9 \(\left( {5\; + \;4\; = \;9} \right)\). Les élèves qui comprennent le concept de la table de 9, mais qui ont du mal à retenir les faits numériques en pratique peuvent bénéficier de la méthode « digitale » illustrée ci-dessous.
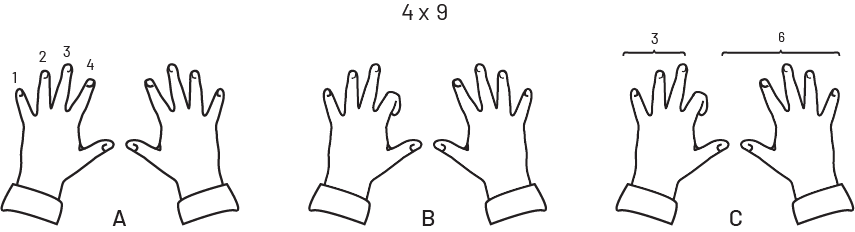 image
4 fois 9.Image A: On voit 2 mains paumes devant. Les dix doigts sont numérotés de, un à dix de la gauche vers la
droite.Image B: le doigt numéro 4 (parenthèse ouvrante) l’index de la main gauche (parenthèse fermante) est
replié.Image C: Le doigt numéro 4 est replié. Un crochet montrant les doigts un à 3 sur lequel est inscrit le chiffre
3.Un autre crochet montrant les doigts 5 à dix sur lequel est inscrit le chiffre 6.
image
4 fois 9.Image A: On voit 2 mains paumes devant. Les dix doigts sont numérotés de, un à dix de la gauche vers la
droite.Image B: le doigt numéro 4 (parenthèse ouvrante) l’index de la main gauche (parenthèse fermante) est
replié.Image C: Le doigt numéro 4 est replié. Un crochet montrant les doigts un à 3 sur lequel est inscrit le chiffre
3.Un autre crochet montrant les doigts 5 à dix sur lequel est inscrit le chiffre 6.
Un certain nombre d’élèves trouvent utile cette méthode kinesthésique pour se rappeler la table de 9. On demande aux élèves de tenir leurs mains devant eux, doigts écartés comme dans l’illustration. Leurs doigts (depuis le petit doigt de la main gauche) sont numérotés de 1 à 10 (A). Elles et ils doivent plier le doigt qui représente le multiplicateur de 9. Ainsi, dans la multiplication \(9\; \times \;4\), c’est le doigt numéro 4, soit l’index de la main gauche, qui est plié (B). Le nombre de doigts qui se trouvent à gauche du doigt plié représente le chiffre des dizaines, le nombre de doigts qui se trouvent à droite du doigt plié représente le chiffre des unités. Ainsi, dans cet exemple les 3 doigts à gauche du doigt numéro 4 représentent 3 dizaines, donc 30, et les 6 doigts à droite du doigt numéro 4 représentent 6 unités, donc 6, ce qui donne 36 (C).
La moitié puis le double
Supposons que l’élève ne peut pas se rappeler un fait numérique donné qui ne comprend que des facteurs pairs. Une méthode de rechange consiste à prendre la moitié de l’un des facteurs pour trouver le produit et ensuite à doubler ce produit. Par exemple, s’il est difficile de se rappeler ce que font \(6\; \times \;8\), il suffit de prendre la moitié de l’un des facteurs \(\left( {3\; \times \;8\; = \;24} \right)\) et de doubler le produit \(\left( {2\; \times \;24} \right)\) pour arriver à la réponse, soit 48. Les élèves devraient explorer cette stratégie en utilisant des dispositions rectangulaires leur offrant une représentation visuelle. Parfois, ces stratégies peuvent sembler un peu lourdes, mais elles offrent aux élèves une façon d’arriver à la bonne réponse par le raisonnement en partant de faits connus. (Van de Walle et Folk, 2005, p. 152, traduction libre)
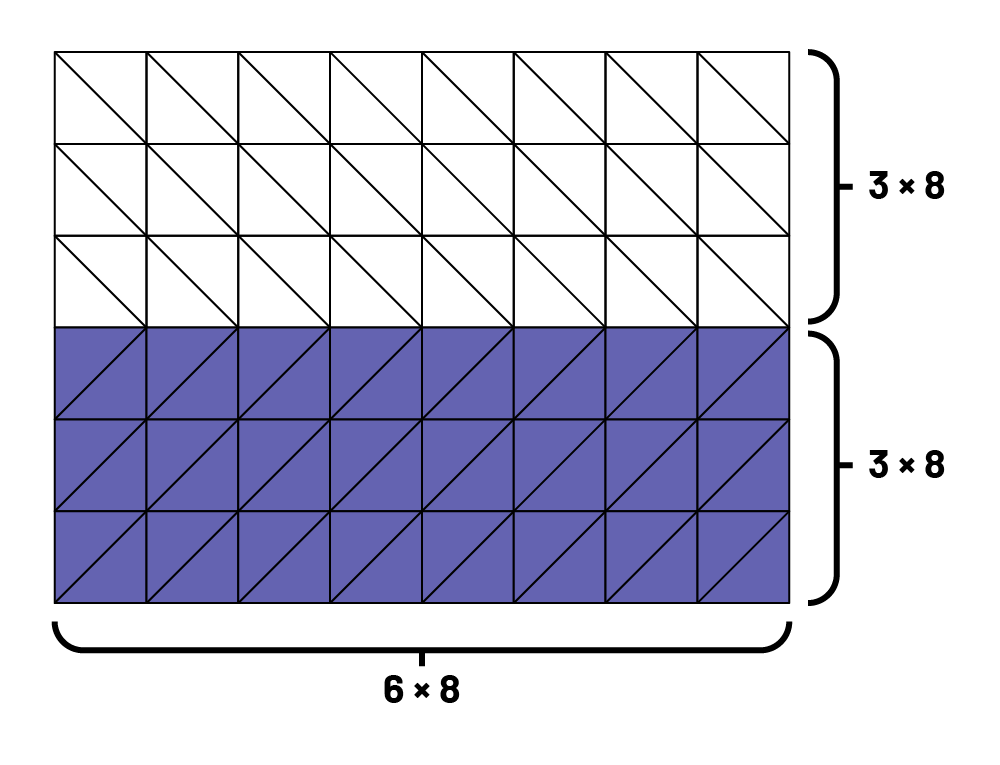 image
Un rectangle divisé en 48 petits carrés dont la moitié inférieure est mauve.Les 3 premières rangées du rectangle sont
indiquées par un crochet qui décrit l’opération 3 fois 8.Les 3 dernières rangées mauves du rectangle sont indiquées
par un crochet qui décrit l’opération 3 fois 8.Un crochet indique les 8 colonnes du rectangle et indique l’opération 6
fois 8.
image
Un rectangle divisé en 48 petits carrés dont la moitié inférieure est mauve.Les 3 premières rangées du rectangle sont
indiquées par un crochet qui décrit l’opération 3 fois 8.Les 3 dernières rangées mauves du rectangle sont indiquées
par un crochet qui décrit l’opération 3 fois 8.Un crochet indique les 8 colonnes du rectangle et indique l’opération 6
fois 8.
La relation inverse de la division et de la multiplication
Les élèves qui maîtrisent les faits numériques de multiplication devraient se servir de ces acquis pour découvrir les faits numériques de division. Il est recommandé d’enseigner simultanément la division et la multiplication afin de mettre en évidence les relations entre les deux. Lorsque les élèves unissent 4 groupes de 5 éléments pour un total de 20, le personnel enseignant devrait les encourager à se rendre compte que lorsque ce total est à nouveau réparti entre 4 groupes, chaque groupe compte 5 éléments.
La séquence d’apprentissage des faits numériques de base relatifs à la division
Une séquence suggérée pour enseigner les faits relatifs à la division consiste à commencer par les faits relatifs à la division par 2, puis la division par 1, par 5, par 3, par 4, par 6, par 7, par 8 et par 9.
Source : Guide d'enseignement efficace des mathématiques de la maternelle à la 6e année, p. 25-29.
