B2. Sens des opérations
Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne.
Situation d’apprentissage : gomme santé!
Durée totale : environ 90 minutes
| Attente | Contenus d'apprentissage |
|
B2. Sens des opérations Utiliser ses connaissances des nombres et des opérations pour résoudre des problèmes mathématiques de la vie quotidienne. |
B2.2 Se rappeler les faits de multiplication de \(1 \times 1\) à \(10 \times 10\) et les faits de division associés, et démontrer sa compréhension de ces faits.
B2.6 Représenter et résoudre des problèmes relatifs à la division d’un nombre naturel à deux ou à trois chiffres par un nombre naturel à un chiffre, en exprimant le reste sous forme de fraction, si nécessaire, à l’aide d’outils appropriés, y compris de dispositions rectangulaires. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves à :
- reconnaître à quel sens de la division une situation donnée fait appel : au sens « groupement » (division dans laquelle le nombre de groupes est inconnu) ou au sens « partage » (division dans laquelle la taille des groupes est inconnue) ;
- développer des stratégies ou des algorithmes personnels de division.
Dans cette situation d’apprentissage, les élèves explorent le concept de division en résolvant un problème dans le contexte de la fabrication et de l’emballage d’un produit.
| Contexte pédagogique | Préalables |
|---|---|
| Au cycle primaire, les élèves sont initiés à la division, dans un contexte de résolution de problèmes et à l’aide de matériel concret, en effectuant une soustraction répétée de groupes d’objets en ensembles égaux. Les élèves développent une compréhension des faits numériques de base relatifs à la division jusqu’à 100. En 4e année, les élèves utilisent des stratégies personnelles et leurs connaissances antérieures pour résoudre des problèmes de division d’un nombre naturel à trois chiffres par un nombre naturel à un chiffre. | La présente situation d’apprentissage expose les élèves à deux situations problèmes différentes qui font appel à la division. En comparant chacune des deux situations et en utilisant divers algorithmes pour les résoudre, les élèves développent leur compréhension du concept de division.
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :
|
Vocabulaire mathématique
quotient, diviseur, dividende, table de valeurs
Matériel
- annexe 4.1 (Usine de gommes à mâcher) (1 copie par équipe)
- tableau interactif
- grandes feuilles de papier (1 feuille par équipe)
- matériel de manipulation (par exemple, cubes emboîtables, jetons, matériel de base dix, réglettes Cuisenaire)
Avant l’apprentissage (mise en train)
Durée : environ 15 minutes
Demander aux élèves si elles et ils ont déjà visité une usine de fabrication et d’emballage d’un produit quelconque (par exemple, usine de fabrication de chocolat, usine d’embouteillage d’eau) ou si elles et ils ont déjà vu un reportage à la télévision à ce sujet.
Discuter avec eux des différents formats d’emballage retenus par les fabricants (par exemple, tablette de chocolat présentée sous forme de 4 bâtonnets ou de 8 petits carrés, bouteilles d’eau emballées dans une caisse de 12 ou de 24).
Présenter la mise en situation suivante dans un contexte intéressant. Par exemple, dire aux élèves :
L’autre jour, j’ai vu un reportage à la télévision au sujet du virage santé que compte prendre un fabricant de gommes à mâcher. Le fabricant effectue des essais afin de développer des gommes à mâcher qui auraient une saveur originale et qui seraient enrichies de vitamines et de minéraux. Pour que ce nouveau produit se démarque des autres gommes à mâcher présentement sur le marché, il prévoit le vendre dans un emballage contenant 8 gommes de saveurs différentes.
En groupe classe, demander aux élèves de suggérer des saveurs originales pour les gommes (par exemple, bleuet, carotte, yogourt aux bananes, muffin au son, thé vert, miel et citron, petits fruits, mangue). Parmi toutes les suggestions reçues, convenir avec eux d’une sélection de 8 saveurs.
Note : La sélection par les élèves des 8 saveurs rend la situation d’apprentissage plus engageante et facilite la résolution de la seconde partie du problème.
Demander aux élèves d’imaginer que le fabricant accepte de fabriquer ses paquets de gommes à mâcher en utilisant les 8 saveurs choisies par la classe, à savoir que chaque paquet du nouveau produit comprendra 8 gommes de saveurs différentes. Présenter le problème de l’annexe 4.1 au tableau interactif ou sur une grande feuille aux élèves.
S’assurer que les élèves comprennent bien les deux parties du problème, en leur demandant de les expliquer en leurs propres mots. Pour rendre le problème plus concret, montrer un paquet de 8 gommes à mâcher ou en dessiner un modèle au tableau.
Pendant l’apprentissage (exploration)
Durée : environ 55 minutes
Grouper les élèves par deux et leur distribuer une copie de l’annexe 4.1. Mettre à leur disposition du matériel de manipulation, des feuilles et du papier quadrillé.
Observer les élèves et les appuyer dans leur travail sans toutefois leur dire comment relever le défi. Il faut les amener, par des interventions stratégiques, à réfléchir :
- aux stratégies à utiliser pour résoudre chacune des deux parties du problème;
- à ce qui est inconnu dans chacune des deux parties.
Accorder suffisamment de temps pour permettre aux élèves d’explorer diverses stratégies de résolution de problèmes et d’en discuter.
Circuler et poser des questions telles que :
- Comment pouvez-vous représenter cette situation autrement?
- Comment pouvez-vous vous assurer que cette solution est vraie?
- Pourquoi votre stratégie fonctionne-t-elle?
Note : Si les élèves connaissent l’algorithme usuel de la division, leur suggérer de résoudre le problème en utilisant une stratégie différente et d’effectuer ensuite l’algorithme usuel pour vérifier le résultat.
Voici quelques stratégies que les élèves peuvent suggérer pour résoudre chacune des parties du problème.
Partie 1 : Combien de paquets de gommes le fabricant obtiendra-t-il?
Les élèves peuvent :
- effectuer des soustractions répétées;

Exemple
\(\begin{array}{l}208\; - \;8\; = \;200\\200\; - \;8\; = \;192\\192\; - \;8\; = \;184\\ \ldots \\8\; - \;8\; = \;0\end{array}\)
Elles et ils comptent ensuite combien de fois elles et ils ont soustrait 8.
- construire une table de valeurs;
Exemple
| Nombre de paquets | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 20 | 26 |
| Nombre de gommes | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 160 | 208 |
Note : Dans l’exemple ci-dessus, les élèves ont utilisé la stratégie du double en passant de 10 à 20 paquets de gommes.
- utiliser du matériel de manipulation, des illustrations ou du papier quadrillé pour représenter des groupements de 8.
Exemple

Partie 2 : Combien de gommes de chacune des saveurs doit-il fabriquer?
Les élèves peuvent distribuer des gommes, individuellement ou par groupes, selon les 8 saveurs :
- avec du matériel de manipulation, par exemple, des cubes emboîtables de différentes couleurs;
Exemple

- de façon symbolique
Exemple
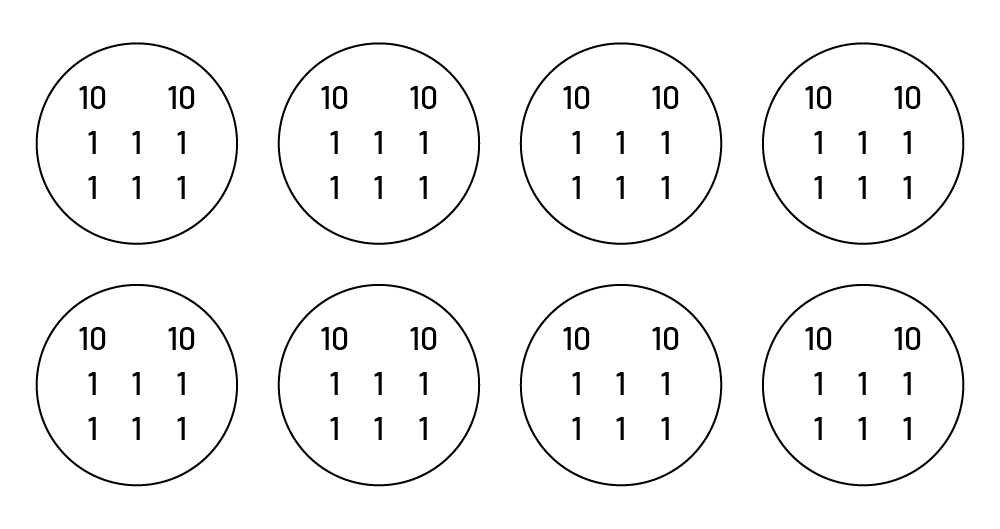
Les élèves peuvent aussi utiliser le même mode de représentation pour les deux parties. Dans l’exemple ci-après, les élèves ont d’abord utilisé du papier quadrillé pour représenter le matériel de base dix (planchettes et cubes d’unité). Les élèves ont représenté le nombre 208 en dessinant 2 planchettes et 8 cubes d’unité. Des groupes de 8 petits carrés chacun ont ensuite été formés et les élèves ont compté 26 groupes (partie 1). Puis, les élèves ont numéroté les carrés de 1 à 8 dans chacun des groupes pour représenter les 8 saveurs (partie 2). Les élèves ont ensuite compté qu’il y avait 26 fois la saveur 1, 26 fois la saveur 2, etc.
Exemple

| Observations possibles | Interventions possibles |
|---|---|
| Des équipes ont de la difficulté à énoncer une phrase mathématique correcte pour justifier le calcul lorsque les élèves combinent des groupes de 8 (par exemple, \(16\; + \;16\; + \;16\; = \;6\;{\rm{groupes}}\)). | Séparer les groupes avec eux à l’aide de cubes emboîtables et les inciter à revoir la phrase mathématique. |
| Certaines équipes utilisent des languettes pour représenter des groupes, mais oublient qu’une languette représente 10 unités alors que le problème présuppose des groupements de 8. | Les inviter à comparer le nombre de cubes d’unité dans une languette avec le nombre de gommes dans un paquet. |
| Une équipe a de la difficulté à faire la différence entre le nombre de gommes par paquet et le nombre de gommes de chaque saveur. | Suggérer aux élèves d’utiliser des cubes d’unité de même couleur pour représenter les gommes dans un paquet (partie 1) et des cubes emboîtables de 8 couleurs différentes pour représenter les 8 saveurs (partie 2). |
| Certaines équipes soulignent que la réponse (26) est la même pour les deux parties du problème sans faire de distinction entre 26 paquets de 8 gommes et 26 gommes de chacune des 8 saveurs. | Les inviter à explorer le problème avec le matériel de manipulation.
Poser des questions telles que :
|
Une fois les deux parties du problème résolues, demander aux élèves de préparer une présentation pour l’échange mathématique.
Leur préciser de :
- noter leurs essais et leurs stratégies sur une grande feuille;
- garder le matériel de manipulation utilisé pour appuyer leur présentation;
- utiliser des arguments mathématiques clairs et convaincants.
Circuler et choisir les équipes qui présenteront lors de l’échange mathématique.
Cibler des équipes qui ont utilisé des stratégies de calcul différentes.
Note : Le choix des équipes qui doivent présenter leur solution est très important puisque c’est par l’entremise des différentes présentations que les élèves peuvent comparer leurs stratégies, compléter leur objectivation et, du même coup, vérifier leur compréhension du concept de division.
Après l’apprentissage (objectivation/transfert de connaissances)
Durée : environ 20 minutes
Discuter d’une partie du problème à la fois. Demander aux équipes sélectionnées de venir, à tour de rôle, présenter leur démarche. Après chaque présentation, les autres élèves contribuent à la communication et enrichissent l’échange mathématique en posant des questions et en faisant des observations pertinentes dans un climat de respect.
Encourager les élèves à utiliser un vocabulaire précis et des termes de causalité. Les inciter à réfléchir en posant, au besoin, des questions telles que :
- Qui peut expliquer dans ses mots la stratégie qu’on vient de présenter?
- Est-ce une stratégie efficace?
- Est-ce que d’autres élèves ont utilisé cette stratégie ou une stratégie similaire?
- Quelles sont les similitudes entre les stratégies utilisées par ces deux équipes (par exemple une équipe qui fait des groupements de 8 et une équipe qui utilise une table de valeurs)?

Lorsque les équipes sélectionnées ont terminé leur présentation, faire ressortir les ressemblances et les différences entre les deux parties du problème en posant des questions telles que :
- Qu’y a-t-il d’inconnu dans la première partie? dans la seconde?
- En quoi les deux parties du problème sont-elles similaires? différentes?
S’assurer de faire ressortir :
- que la division implique de séparer la totalité d’une quantité donnée en groupes égaux;
- que l’on peut utiliser diverses stratégies pour effectuer une division ;
- que l’on retrouve deux sens à la division, le sens « partage » et le sens « groupement ». (Il n’est pas nécessaire que les élèves connaissent ces termes; il leur suffit de comprendre que le quotient peut représenter deux types de quantité.)
Il est aussi important de souligner qu’il est possible de représenter chacune des deux parties du problème à l’aide de l’équation \(208\; \div \;8\; = \;26\). Ce qui est différent, c’est le sens qu’on accorde aux nombres dans chaque équation :
- Dans la partie 1, il y a lieu d’écrire : 208 gommes ÷ 8 gommes par paquet = 26 paquets.
- Dans la partie 2, il y a lieu d’écrire : 208 gommes ÷ 8 saveurs = 26 gommes de chaque saveur.
Note : Mentionner les termes propres à la division tels que le quotient, le diviseur et le dividende.
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
| Diminuer le nombre de gommes produites (par exemple, 104 au lieu de 208). | Demander aux élèves de représenter, pour chacune des deux parties du problème à l’aide d’une disposition rectangulaire sur papier ou à l’aide de cubes emboîtables, comment les 208 gommes à mâcher peuvent être placées lorsqu’elles sortent de la première machine. |
Suivi à la maison
Demander aux élèves de résoudre, à la maison, de deux façons différentes le problème suivant ou un problème similaire sans utiliser la calculatrice et d’expliquer leurs démarches à un membre de la famille.
Pour une fête, je dois préparer des sacs de guimauves. Dans chaque sac, je compte mettre 6 guimauves. Si j’ai 108 guimauves en tout, combien de sacs pourrais-je préparer?
Note : Cette activité permet aux parents de voir qu’il est possible d’effectuer une division sans utiliser l’algorithme usuel.
Activité supplémentaire – Construction de structures
Présenter un problème en deux parties, semblable à celui de la situation d’apprentissage, afin que les élèves puissent utiliser les diverses stratégies présentées lors de l’échange mathématique.
Exemple
Le personnel enseignant demande à ses élèves de construire une structure en se servant de cubes emboîtables.
Le personnel enseignant demande à Éric de distribuer 196 cubes emboîtables à 7 équipes. Combien de cubes emboîtables Éric doit-il remettre à chaque équipe si chacune doit recevoir le même nombre de cubes?
Le personnel enseignant demande ensuite aux équipes d’échanger leurs structures et d’utiliser un autre ensemble de cubes emboîtables pour construire une structure identique à celle reçue. Pour ce faire, elle demande à Louise de distribuer 196 autres cubes aux équipes. Elle remet à Louise une boîte pleine de petits sacs contenant 7 cubes chacun. Combien de sacs Louise doit-elle prendre si elle veut s’assurer de distribuer 196 cubes en tout?
Lorsque les équipes ont terminé, mener un échange mathématique afin de faire ressortir les différentes stratégies utilisées. Comme dans la situation d’apprentissage précédente, demander aux élèves d’expliquer ce que les nombres représentent dans chacune des deux parties du problème.
Source : Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 167-176.
