B1.6 Arrondir les nombres décimaux au dixième près, dans divers contextes.
Habileté : arrondir les nombres décimaux au dixième près, dans divers contextes
Dans la plupart des situations de la vie courante, il n’est pas nécessaire de travailler avec un nombre précis, puisqu’une approximation est tout aussi valable et souvent plus commode. Les élèves du cycle moyen doivent pouvoir arrondir en utilisant leur sens du nombre, ce qui nécessite une analyse et une réflexion.
Des problèmes variés doivent être présentés aux élèves pour les inciter à réfléchir à l’effet de l’arrondissement sur la quantité et à choisir la façon d’arrondir. Doit-on arrondir à l’unité près ou au dixième près? Le choix dépend du contexte, du sens du nombre et des raisons qui poussent à arrondir. Par exemple, une restauratrice qui possède des tables d’une longueur de 2,27 m peut, lors de l’achat de nappes, arrondir la longueur à 2,3 m ou même à 2,5 m pour être certaine que les nappes achetées seront assez longues. Cependant, lorsqu’elle en parle à ses employés, elle peut s’y référer en parlant des tables de 2 m. Bref, c’est seulement après une analyse du contexte qu’on peut déterminer comment effectuer l’arrondissement ou à quelle position l’arrondissement doit se faire.
Malheureusement, l’arrondissement est trop souvent enseigné à l’aide de méthodes qui sont vides de sens, car elles traitent des chiffres et non pas de la quantité. Par exemple, pour arrondir un nombre décimal au dixième près, les élèves apprennent à identifier le chiffre dans la position à arrondir, puis à considérer le chiffre qui le suit. Si celui-ci est supérieur ou égal à 5, le chiffre identifié est augmenté de 1 et les chiffres qui suivent sont éliminés.
Exemple
Des résultats d’études révèlent que ces méthodes traditionnelles d’arrondissement ne développent pas le concept d’approximation chez l’élève.
Note : Puisque pour arrondir un nombre décimal, les élèves doivent utiliser leur sens du nombre décimal, il est important qu’au préalable, ils aient eu l’occasion de le développer en représentant des nombres décimaux, en les situant sur une droite numérique et en les comparant.
Exemple
Pour arrondir 6,28 à l’unité près, les élèves reconnaissent que le nombre 6,28 représente une quantité équivalente à « 6 et un peu plus ». Elles et ils savent alors que le nombre se situe entre 6 et 7. Elles et ils utilisent ensuite leur sens du nombre pour déterminer si 6,28 est plus près de 6 ou de 7. Elles et ils peuvent, par exemple, utiliser un nombre repère représentant le milieu de l’intervalle (6,5 ou 6,50), « voir » que 6,28 c’est près de 6,2 ou de 6,3 ou même visualiser l’emplacement de 6,28 sur une droite numérique.
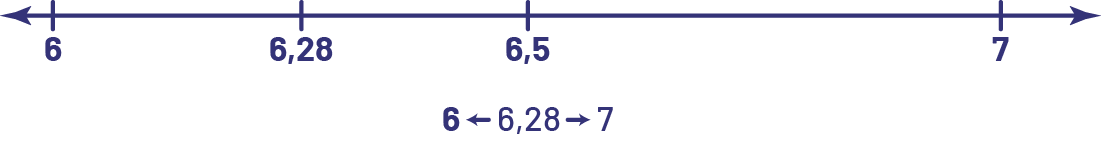
Peu importe l’élément du sens du nombre choisi, les élèves sont alors en mesure d’arrondir 6,28 à 6. Si elles et ils décident d’arrondir plutôt au dixième près, elles et ils doivent utiliser leur compréhension de la quantité représentée par ce nombre et reconnaître que 6,28 représente une quantité qui se situe entre 6,2 et 6,3.
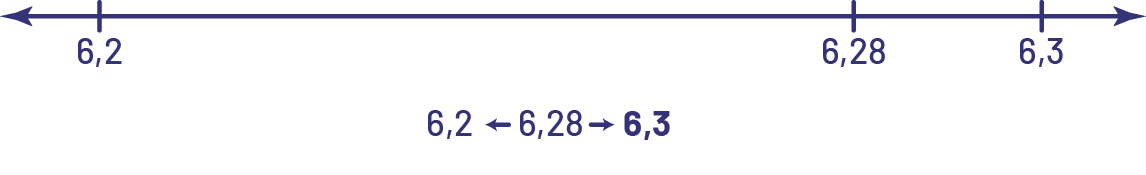image
Droite numérique graduée de 6 virgule 2 à 6 virgule 3. Le nombre 6 virgule 28 est inscrit plus près de 6 virgule
3.Dessous on démontrer que 6 virgule 28 est situé entre 6 virgule 2 et 6 virgule 3. Le nombre 6,28 situé à droite du
nombre 6 virgule 2 et à gauche du nombre 6 virgule 3.Une flèche part du nombre 6 virgule 28 et pointe 6 virgule 2 à
gauche.Une autre flèche part de 6 virgule 28 et pointe 6 virgule 3 à droite.
En visualisant le nombre 6,28 sur une droite, les élèves peuvent conclure que 6,28 est plus près de 6,3 que de 6,2 et donc, arrondir 6,28 à 6,3.
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 44.