E1.4 Donner et suivre des directives à étapes multiples, incluant des distances ainsi que des demi-tours et des quarts de tour, pour effectuer un déplacement d’un endroit à un autre.
HABILETÉ : DONNER ET SUIVRE DES DIRECTIVES
L’enfant reconnaît peu à peu le chemin pour se rendre de la maison à l’école. À titre d’exemple, elle ou il remarque un certain commerce situé près de sa maison ou un certain restaurant près de chez sa gardienne. À partir de ses points de repère, l’enfant peut se situer et se déplacer dans son environnement.
En 3e année, l’élève peut utiliser un réseau simple pour décrire des déplacements. Il ou elle peut décrire différents trajets pour se rendre d’un point à un autre, en précisant le point de départ, le point d’arrivée et la direction du déplacement. L’élève peut aussi préciser la position de certains endroits les uns par rapport aux autres en utilisant le vocabulaire des relations spatiales.
Exemple
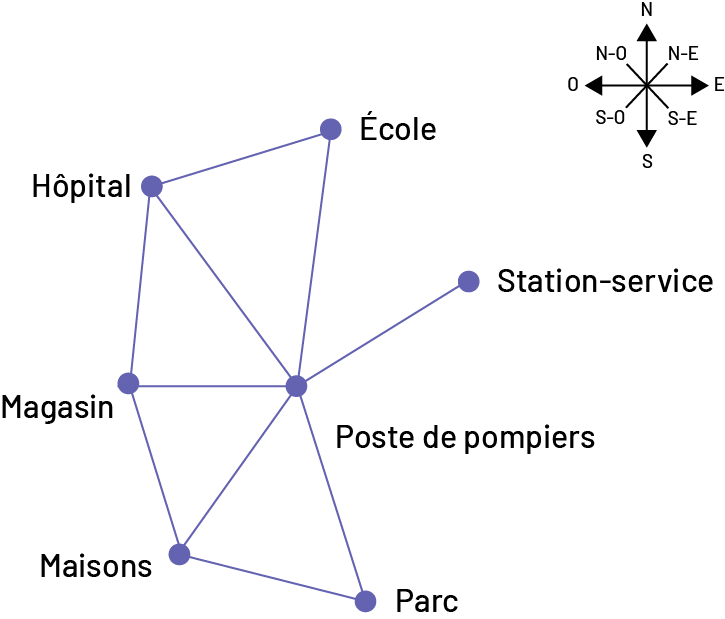Image Réseau simple de déplacements. Le point central du réseau est le
poste de pompiers, de ce point il y a un tracé pour toutes les autres
destinations dont le poste de pompiers est le départ : station-service, l’école, l’hôpital, le magasin, la maison.
Le réseau est accompagné d’une rose des vents.
- Pour me rendre de l’école au parc, je dois passer par le poste de pompiers.
- L’hôpital est au nord-ouest du poste de pompiers.
- Le magasin est au sud de l’hôpital.
« Certains termes utilisés pour décrire la position d’un objet sont relatifs à d’autres (près de, loin de), tandis que d’autres termes sont absolus (nord, est). »
(National Council of Teachers of Mathematics, 2001, p. 31, traduction libre)
La communication, le modelage et les contes devraient être utilisés pour faciliter l’apprentissage des habiletés relatives aux relations spatiales. À titre d’exemple, lors de la mise en scène d’un conte comme Boucle d’or et les Trois Ours, les élèves utilisent des termes de relations spatiales (par exemple, Boucle d’or s’assoit sur la grosse chaise, s’avance près du lit). Peu à peu, les élèves réalisent qu’elles et ils sont en relation constante avec leur environnement. Le personnel enseignant utilise alors la classe ou l’école comme point de repère pour créer des réseaux de plus en plus complexes.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 58-59.
HABILETÉ : EFFECTUER UN DÉPLACEMENT
« Les élèves utilisent naturellement leurs expériences avec les objets pour comprendre les transformations telles que la translation, la réflexion et la rotation. »
(National Council of Teachers of Mathematics, 2000, p. 99, traduction libre)
L’enfant arrive à l’école avec des expériences de déplacements. Elle ou il en effectue inconsciemment depuis sa naissance. Au fil des ans, le vocabulaire de l’enfant évolue et lui permet de décrire avec plus de précision les déplacements effectués.
Translation
Avant la 4e année, l’élève effectue des translations sans savoir que ce sont des translations. Par exemple, elle ou il range des objets, change la position de divers objets et se déplace d’un endroit à l’autre. Le personnel enseignant lui donne des directives afin qu’elle ou il puisse se déplacer pour aller chercher un objet, se rendre aux toilettes ou au bureau de la secrétaire.
En 1re année, l’élève décrit des déplacements dans une grille à l’aide de quatre directions : vers la droite, vers la gauche, vers le haut et vers le bas. Elle ou il peut décrire un déplacement en fonction de la distance et de la direction en utilisant des mots ou des symboles.
Exemple
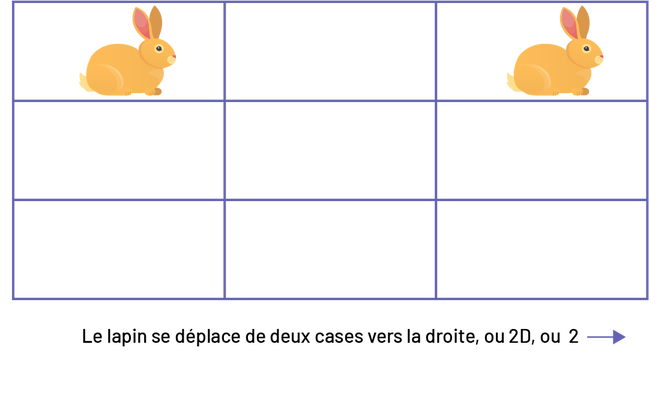
En 2e année, l’élève apprend à exprimer le déplacement de façon plus précise. Elle ou il effectue des déplacements horizontaux et verticaux sur une grille. L’élève utilise un système de repérage en décrivant la direction (vers la droite, vers la gauche, vers le haut, vers le bas) et la distance (nombre de cases).
Exemple
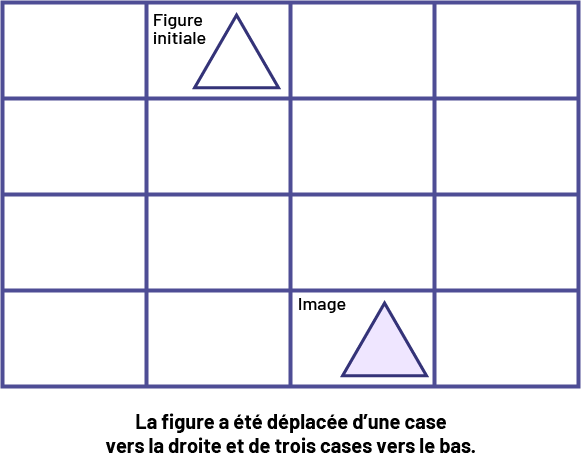Image Une grille de 4 colonnes et de 4 rangées. Un triangle « figure
initiale est placé dans la première case de la deuxième colonne. Le triangle « image » est placé dans la dernière case
de la troisième colonne.
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 59-61.
Rotation
En 3e année, le concept de rotation s’ajoute aux déplacements. L’amplitude d’une rotation se rapporte à la mesure des angles, une aptitude développée plus formellement en 4e et en 5e année. En 3e année, le vocabulaire associé aux demi-tours et aux quarts de tour correspond aux mouvements de l’aiguille des minutes d’une horloge analogique. Un tour peut s’effectuer dans le sens horaire (sens des aiguilles d’une montre) ou antihoraire (sens inverse des aiguilles d’une montre).
Un tour complet correspond à un déplacement circulaire à la fin duquel un objet est orienté dans la même direction qu’au début, comme dans le cas d’une aiguille qui commence et qui termine son tour à 12 heures. Un tour complet produit le même résultat, peu importe le sens dans lequel il est effectué.
Un demi-tour correspond à un déplacement à la fin duquel un objet est orienté dans la direction opposée par rapport à celle du début, comme dans le cas d’une aiguille qui commence son tour à 12 heures et qui le termine à 6 heures. Un demi-tour produit le même résultat, peu importe le sens dans lequel il est effectué.
Un quart de tour oriente un objet dans une direction correspondant à 9 heures ou à 3 heures. Par exemple, une aiguille qui se trouve initialement à 12 heures et qui effectue un quart de tour vers la droite s’arrêtera à 3 heures. Si elle fait un quart de tour vers la gauche, elle s’arrêtera à 9 heures.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.