E1.1 Déterminer les propriétés géométriques des polygones qui forment des dallages ainsi que les transformations géométriques qui se produisent.
HABILETÉ : DÉTERMINER LES PROPRIÉTÉS GÉOMÉTRIQUES DES POLYGONES QUI FORMENT DES DALLAGES AINSI QUE LES TRANSFORMATIONS GÉOMÉTRIQUES QUI SE PRODUISENT
Il est primordial de comprendre qu’un dallage utilise au moins un polygone combiné en une suite à motif répété pour recouvrir un plan sans créer de chevauchement ni laisser d’espace. En raison du fait qu’ils sont des polygones réguliers (les angles et les côtés sont tous identiques), et donc à formes isométriques, seuls les triangles équilatéraux, les carrés et les hexagones réguliers permettent de créer des dallages réguliers par eux-mêmes.
 Image Un
dallage fait de polygones réguliers, ici des triangles. Le dallage est fait de triangles, l’un à l’endroit et le
suivant à l’envers, sur plusieurs rangées.
Image Un
dallage fait de polygones réguliers, ici des triangles. Le dallage est fait de triangles, l’un à l’endroit et le
suivant à l’envers, sur plusieurs rangées.
Il est possible d’utiliser des polygones non réguliers afin de créer des dallages,
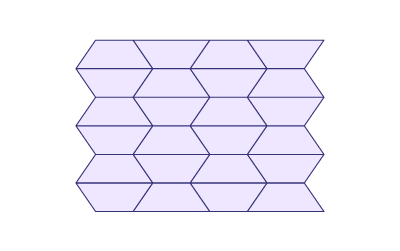

ou d’utiliser au moins deux polygones afin d’éviter des espaces.
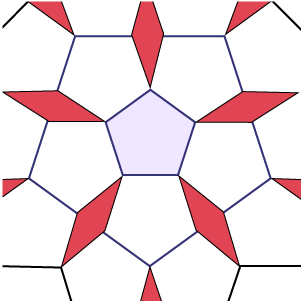
Un dallage construit à l’aide de polygones réguliers est un dallage régulier, et un dallage construit avec au moins deux types de polygones réguliers est un dallage semi-régulier.
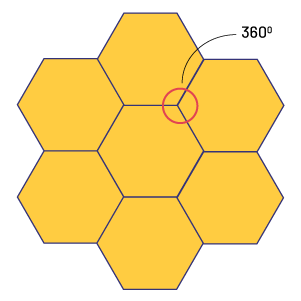
Dans tout dallage, la somme des angles où les polygones se rejoignent est de 360°, c’est-à-dire que tout l’espace autour de ce point de rencontre est occupé.
Des dallages complexes peuvent être conçus en décomposant les figures géométriques en polygones et en réorganisant les polygones par une combinaison de translations, de réflexions et de rotations. Si le polygone reste inchangé, il est symétrique et sert à former des dallages réguliers et semi-réguliers.
On trouve des dallages dans le domaine des arts, de la décoration et du paysagement, sur des tapisseries, des tapis, des mosaïques, des couvre-planchers et dans l’utilisation de pierres de pavage.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Certains outils sont utiles pour aider les élèves à mieux comprendre les transformations et à voir les résultats de diverses transformations au moment de la création de dallages. C’est le cas, entre autres, du papier à points, du papier quadrillé et du papier calque.
Le Mira est particulièrement utile au moment de la réflexion de figures géométriques.
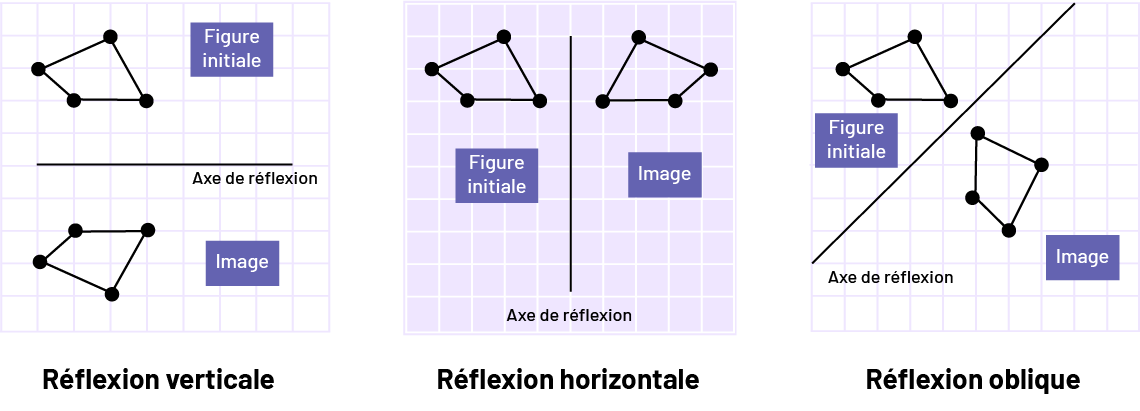 image Sur
une surface quadrillée est placée une figure initiale, deux cases en dessous, un axe de réflexion et deux cases en
dessous, une image. C’est une réflexion verticale.Sur une surface quadrillée est placée à la gauche, une figure
initiale, à une case sur la droite, un axe de réflexion et une case sur la droite, une image. C’est une réflexion
horizontale.Sur une surface quadrillée est placée dans le coin à gauche, une figure initiale. Le sommet, de la figure
initiale, le plus près de l’axe de réflexion est placé sur le même carré que le sommet de l’image le plus prêt de
l’Axe. L’axe de réflexion est placé en diagonale , il traverse le cube commun des deux figures et le divise en parties
égales. C’est une réflexion oblique.
image Sur
une surface quadrillée est placée une figure initiale, deux cases en dessous, un axe de réflexion et deux cases en
dessous, une image. C’est une réflexion verticale.Sur une surface quadrillée est placée à la gauche, une figure
initiale, à une case sur la droite, un axe de réflexion et une case sur la droite, une image. C’est une réflexion
horizontale.Sur une surface quadrillée est placée dans le coin à gauche, une figure initiale. Le sommet, de la figure
initiale, le plus près de l’axe de réflexion est placé sur le même carré que le sommet de l’image le plus prêt de
l’Axe. L’axe de réflexion est placé en diagonale , il traverse le cube commun des deux figures et le divise en parties
égales. C’est une réflexion oblique.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 31.
Le papier à coordonnées polaires, l’équerre et le logiciel Cybergéomètre sont particulièrement utiles pour effectuer la rotation selon la fraction de tour spécifiée; ils aident les élèves à mieux comprendre cette transformation.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 34.
Il est à noter que les élèves consolident leur compréhension des transformations en les comparant et en les utilisant pour créer des frises ou des dallages.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 27.
CONNAISSANCE : DALLAGE
Un dallage utilise des polygones pour recouvrir un plan sans créer de chevauchement ni laisser d’espace. Il est composé d’au moins un polygone combiné en une suite à motif répété. La somme des angles où les polygones se rejoignent est de 360°.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : PROPRIÉTÉS GÉOMÉTRIQUES DES POLYGONES
Pour maîtriser le concept de dallage, certains mots de vocabulaire et certains concepts doivent être bien compris.
Un polygone est une figure plane formée d’une ligne brisée et fermée.
Dans un polygone convexe, tous les angles sont saillants ou la mesure de chaque angle est inférieure à 180°.
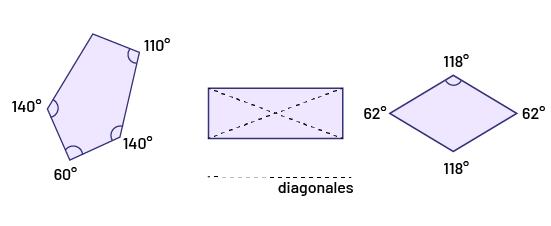 Image Un pentagone irrégulier, les mesures des angles sont, 60 degrés, 140 degrés, 110 degrés, 140
degrés.Un rectangle où sont placées deux diagonales.Un losange, les mesures des angles sont, 110 degrés, 65 degrés,
113 degrés, 113 degrés, 72 degrés.
Image Un pentagone irrégulier, les mesures des angles sont, 60 degrés, 140 degrés, 110 degrés, 140
degrés.Un rectangle où sont placées deux diagonales.Un losange, les mesures des angles sont, 110 degrés, 65 degrés,
113 degrés, 113 degrés, 72 degrés.
Dans un polygone non convexe, un des angles est rentrant et mesure plus de 180°. De plus, l’une des diagonales qui relie deux sommets non consécutifs se trouve à l’extérieur de la figure.
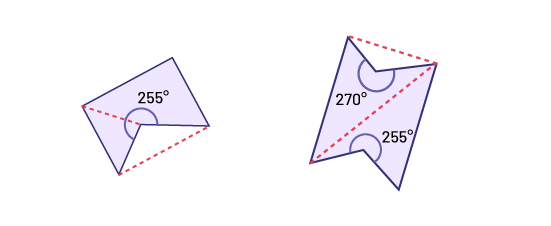 Image Un
polygone non convexe de 5 côtés. Un, des angles est rentrant mesure 225 degrés. Une diagonale est à l’extérieur de la
figure.
Image Un
polygone non convexe de 5 côtés. Un, des angles est rentrant mesure 225 degrés. Une diagonale est à l’extérieur de la
figure.
Polygone régulier : polygone dont tous les côtés et tous les angles intérieurs sont congrus. Le polygone régulier est symétrique et convexe.
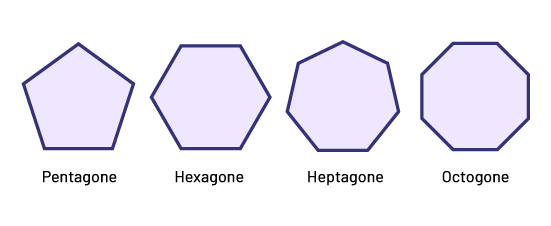
Polygone irrégulier : polygone dont les côtés et les angles intérieurs ne sont pas congrus.
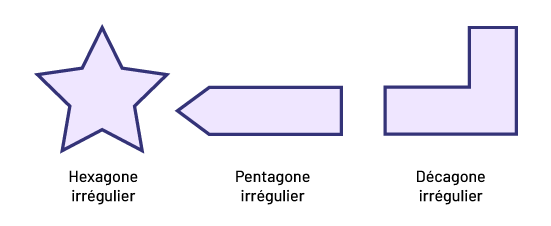
Source: Guide d’enseignement efficace des mathématiques de la 4e à la 6e année, p. 24-26.
CONNAISSANCE : TRANSFORMATION GÉOMÉTRIQUE
Les transformations utilisées au moment de dallages sont les translations, les réflexions et les rotations, qui produisent toutes des images congruentes.
- Une translation « fait glisser » une figure sur une distance donnée et dans une direction donnée.
- Une réflexion « inverse » une figure par rapport à un axe perpendiculaire à une direction donnée, appelé axe de réflexion, pour créer la figure opposée.
- Une rotation « fait tourner » une figure autour d’un centre de rotation selon un angle donné.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
