E2.2 Résoudre des problèmes associés aux propriétés des angles, y compris la propriété des droites sécantes et parallèles et les propriétés des polygones.
HABILETÉ : RÉSOUDRE DES PROBLÈMES ASSOCIÉS AUX PROPRIÉTÉS DES ANGLES
Il est possible de déterminer la mesure des angles en appliquant les propriétés des angles. Il est souvent plus rapide de calculer la mesure des angles que de tenter de les mesurer.
Si un grand angle de mesure donnée est composé de deux plus petits angles, seuls deux d’entre eux sont nécessaires pour trouver la valeur du troisième.
La mesure d’un angle connu permet de déterminer la mesure d’angles inconnus. Voici quelques propriétés des angles :
- Un angle plat mesure 180°; en sachant cela, il est possible de déterminer la mesure d’angles supplémentaires.
- Un angle droit mesure 90°; en sachant cela, il est possible de déterminer la mesure d’angles complémentaires.
- La somme des angles intérieurs d’un triangle est de 180°; la somme des angles intérieurs d’un quadrilatère est de 360°; la somme des angles intérieurs d’un pentagone est de 540°; la somme des angles intérieurs d’un polygone à n côtés est (n – 2) × 180. Les propriétés des angles d’un polygone peuvent servir à trouver la mesure d’un angle manquant.
Remarques
- Le but de ce contenu d’apprentissage n’est pas de mémoriser les propriétés des angles ou les termes, mais plutôt d’avoir recours à un raisonnement spatial et à une connaissance des angles connus pour déterminer des angles inconnus.
- Si deux figures sont semblables, elles ont des angles congrus (voir le contenu d’apprentissage E1.3). Le fait de reconnaître les similarités entre des figures (par exemple, en s’assurant que la longueur de leurs côtés est proportionnelle) peut aussi servir à trouver la mesure d’angles manquants.
- Il est possible d’additionner la mesure de petits angles pour déterminer la mesure d’un plus grand, grâce à la propriété d’additivité.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : PROPRIÉTÉS DES DROITES SÉCANTES ET PARALLÈLES
Des droites sécantes sont des droites qui se coupent en un point.
Des droites parallèles sont deux droites dont la distance qui les sépare reste constante.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Les propriétés présentées ci-dessus peuvent servir à trouver la mesure d’angles inconnus lorsqu’une sécante coupe deux droites parallèles, comme la figure l’indique :
Image Deux droits parallèles sont traversés par une droite sécante. La mesure des angles se fait avec la droite supérieure comme suit, dans le sens contraire des aiguilles d’une montre.Angle « a », angle « b », angle « c », angle « d ».La mesure des angles se fait avec la droite inférieure comme suit, dans le sens contraire des aiguilles d’une montre.Angle « e », angle « f », angle « g », angle « h ».Dans un encadré on peut lire :Les angle alternes internes sont congrus, de sorte que l’angle « c » égal angle « e » et angle « d » égal angle « f ».Les angles opposés sont congrus, de sorte que : angle « b » égal angle « d », angle « a » égal angle « c », angle « f » égal angle « h » et, angle « e » égal angle « g ».Les angles alternes externes sont congrus, de sorte que : angle « b » égal angle « h » et angle « a » égal angle « g ».Les angles correspondants sont congrus, de sorte que : angle « b » égal angle « f », angle « c » égal angle « g », angle « a » égal angle « e » et angle « d » égal angle « h ».La somme des angles intérieurs est de 180 degrés, de sorte que : Angle « c » plus angle « f » égal 180 degrés. Angle « d » plus angle « e », égal 180 degrés. Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : PROPRIÉTÉS DES POLYGONES
La somme des angles intérieurs d’un triangle est de 180°; la somme des angles intérieurs d’un quadrilatère est de 360°; la somme des angles intérieurs d’un pentagone est de 540°; la somme des angles intérieurs d’un polygone à n côtés est (n – 2) × 180. Les propriétés des angles d’un polygone peuvent servir à trouver la mesure d’un angle manquant.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
L’angle intérieur est formé par l’intersection de deux côtés adjacents à l’intérieur d’un polygone. Un polygone à « n » côtés a « n » angles intérieurs.
La somme des mesures (en degrés) des angles intérieurs de tout polygone à « n » côtés est 180° × (n – 2). L’expression (n – 2) représente le nombre de triangles que l’on peut tracer à l’intérieur d’une figure.
Note pédagogique : La formule qui permet de connaître rapidement la somme des angles intérieurs d’un polygone est donnée ici pour le personnel enseignant seulement. Les élèves du cycle intermédiaire ne sont pas tenues et tenus de connaître et d’utiliser ce concept.
\(1 \ \mathrm{triangle} \times 180^{\circ} = 180^{\circ}\)
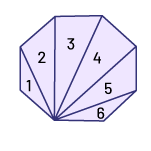
\(6 \ \mathrm{triangles} \times 180^{\circ} = 1 \ 080^{\circ}\)
Remarque
Lorsque les élèves doivent construire un polygone et afficher la mesure des angles, elles et ils doivent vérifier si la somme des angles intérieurs est juste. Vous pouvez afficher au mur un tableau de la somme des angles de divers polygones et demander aux élèves de s’y référer.
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).
L’angle extérieur est formé d’un des côtés d’un polygone et du prolongement de l’un de ses côtés adjacents.
Dans un polygone, l’angle extérieur et l’angle intérieur adjacent sont supplémentaires, c’est-à-dire que leur somme est toujours 180°.
La somme des angles extérieurs d’un polygone est toujours 360°.
Exemples de polygones
Hexagone
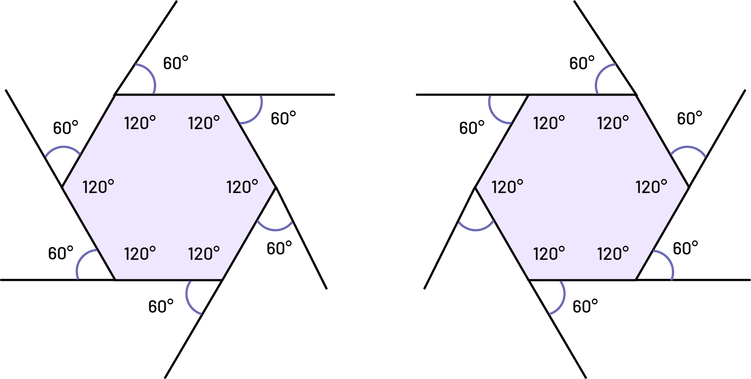image Un hexagone dont tous les segments ont été prolongés sur l’extérieur, dans le sens des aiguilles d’une montre. Les angles qui résultent de ce prolongement sont de 60 degrés. Les angles à l’intérieur de l’hexagone sont de 120 degrés.Un hexagone dont tous les segments ont été prolongés sur l’extérieur, dans le sens contraire des aiguilles d’une montre. Les angles qui résultent de ce prolongement sont de 60 degrés. Les angles à l’intérieur de l’hexagone sont de 120 degrés.\(60^{\circ} + 60^{\circ} + 60^{\circ} + 60^{\circ} + 60^{\circ} + 60^{\circ} = 360^{\circ}\)
Rectangle
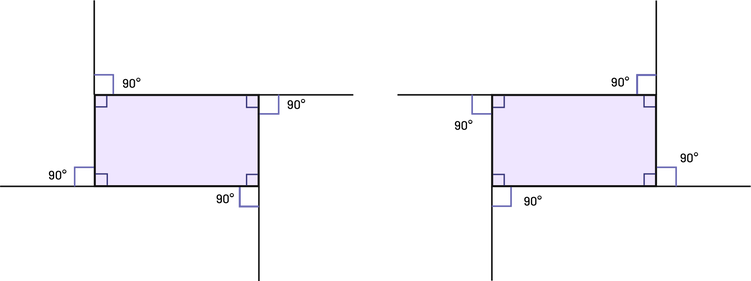image Un rectangle dont tous les segments ont été prolongés sur l’extérieur, dans le sens des aiguilles d’une montre. Les angles qui résultent de ce prolongement sont de 90 degrés.Un hexagone dont tous les segments ont été prolongés sur l’extérieur, dans le sens contraire des aiguilles d’une montre. Les angles qui résultent de ce prolongement sont de 60 degrés. Les angles à l’intérieur de l’hexagone sont de 120 degrés.\(90^{\circ} + 90^{\circ} + 90^{\circ} + 90^{\circ} = 360^{\circ}\)
Triangle
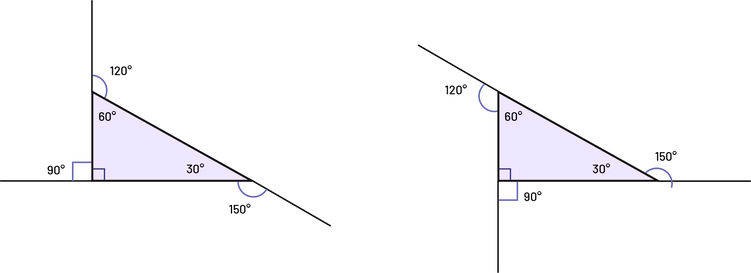image Un triangle dont tous les segments ont été prolongés sur l’extérieur, dans le sens des aiguilles d’une montre. Les angles qui résultent de ce prolongement sont de 120 degrés, 150 degrés et 90 degrés. Les angles à l’intérieur du triangle sont de 60 degrés, 90 degrés et 30 degrés.Un triangle dont tous les segments ont été prolongés sur l’extérieur, dans le sens contraire des aiguilles d’une montre. Les angles qui résultent de ce prolongement sont de 120 degrés, 90 degrés, et 150 degrés. Les angles à l’intérieur du triangle sont 60 degrés, 90 degrés, et 30 degrés.\(90^{\circ} + 120^{\circ} + 150^{\circ} = 360^{\circ}\)
Source : L'@telier - Ressources pédagogiques en ligne (atelier.on.ca).