E2.4 Expliquer le théorème de Pythagore en utilisant divers modèles géométriques et se servir du théorème pour calculer la mesure de longueur manquante d’un côté d’un triangle rectangle donné.
HABILETÉ : EXPLIQUER LE THÉORÈME DE PYTHAGORE EN UTILISANT DIVERS MODÈLES GÉOMÉTRIQUES
Les propriétés d’un triangle rectangle peuvent servir à trouver la longueur inconnue d’un côté. Pour tout triangle rectangle, l’aire d’un carré construit sur son côté le plus long (l’hypoténuse) est égale aux aires combinées des carrés construits sur les deux côtés courts. Cette relation est connue sous le nom de théorème de Pythagore.
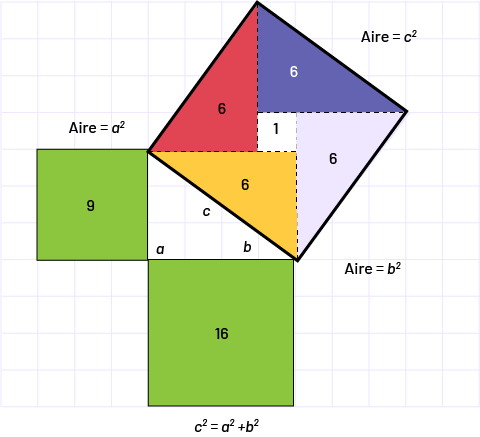image Un
petit carré blanc annoté : un est au centre d’un grand carré. Le reste de la surface de ce carré est divisé en 4
triangles rectangles , ils sont tous annotés : 6. Le côté de ce carré est « c ». Au coin en bas à droite un deuxième
carré, de taille moyenne, est placé, il est annoté 16. Un troisième carré de petite taille, et annoté 9, est placé en
bas à gauche. De cette façon les trois carrés ont créé un espace de forme triangulaire, « a » « b » « c ».Aire du
grand carré égal « c » au carré.Aire du carré moyen égal « b » au carré.Aire du petit carré égal « a » au carré.« c »
au carré égal « a » au carré plus « b » au carré.
Le théorème de Pythagore exprime cette relation de façon symbolique : a2 + b2 = c2. Pour résoudre l’équation, c prend la valeur de la longueur de l’hypoténuse (c) et a et b prennent les valeurs respectives des longueurs des côtés a et b du triangle. Par exemple :
- si le côté a a une longueur de 3 unités, un carré construit sur ce côté a une aire de 32 ou de 9 unités carrées;
- si le côté b a une longueur de 4 unités, un carré construit sur ce côté a une aire de 42 ou de 16 unités carrées;
- si l’aire du carré se trouvant sur le côté c est égale aux aires combinées des carrés se trouvant sur les côtés a et b, le carré sur le côté c a une aire de 25 unités carrées (9 unités carrées + 16 unités carrées);
- si l’aire du carré se trouvant sur le côté c est de 25 unités carrées, la longueur du côté c est de \(\sqrt{25}\) ou 5 unités.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Dans ce genre de problème, l’erreur la plus courante est de ne pas bien identifier le côté le plus long, l’hypoténuse.
HABILETÉ : SE SERVIR DU THÉORÈME POUR CALCULER LA MESURE DE LONGUEUR MANQUANTE D’UN CÔTÉ D’UN TRIANGLE RECTANGLE DONNÉ
La relation inverse entre l’addition et la soustraction signifie que le théorème de Pythagore peut servir à trouver n’importe quelle longueur d’un triangle rectangle (par exemple, c2 - b2 = a2; c2 - a2 = b2).
Le théorème de Pythagore sert à mesurer indirectement des longueurs qui seraient difficiles ou impossibles à mesurer directement. À titre d’exemple, il est très utilisé dans les domaines de la construction, de l’architecture et de la navigation. Par extension, ce théorème permet aussi de mesurer des distances dans l’espace.
Remarques
Les propriétés d’un carré peuvent servir à trouver la longueur de ses côtés ou son aire. La longueur des côtés d’un carré est égale à la racine carrée de son aire. Construire un carré sur un segment est une façon de mesurer indirectement la longueur du segment.
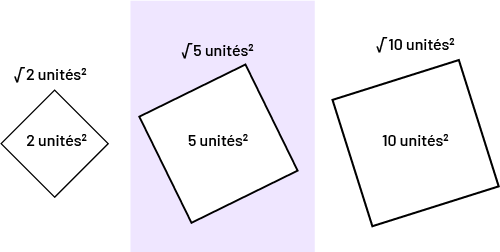Image Un carré de 2 unités au carré, et titré : racine carrée 2 unités au
carré.Un carré de 5 unités au carré, et titré : racine carrée 5 unités au carré.Un carré de dix unités au carré, et
titré : racine carrée dix unités au carré.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Exemple
Détermine la mesure manquante. Arrondis ta réponse au dixième près.
Représentation visuelle
Il s’agit d’un triangle rectangle. Je sais que, pour tout triangle rectangle, la relation de Pythagore implique que l’aire d’un carré construit sur son côté le plus long (l’hypoténuse) est égale aux aires combinées des carrés construits sur les deux côtés adjacents à l’angle droit.
Étant donné que je dois trouver la longueur du côté b, je dois soustraire l’aire du carré du côté a de l’aire du carré de l’hypoténuse.
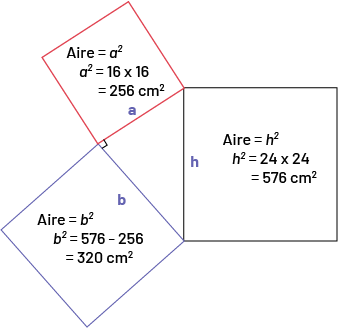Image Un
carré dont sommet à la droite du segment « a » touche le haut du segment « h » d’un deuxième carré. Le bas du segment
«h » de ce deuxième carré touche la droite d’un segment nommé « b » d’un troisième carré. Ce dernier touche la gauche
du segment « a » du premier carré.Ainsi placés les carrés forment un triangle « a » « h » « b ». L’angle « a » « b »
est un angle droit.Aire du premier carré est « a » au carré.« a » au carré égal 16 multiplié par 16, égal 256
centimètres carrés.L’aire du deuxième carré égal « h » au carré. « h » au carré égal 24 multiplié par 24, égal 576
centimètres carrés.L’aire du troisième carré égal « b » au carré. « b » au carré égal 576 moins 256, égal 320
centimètres carrés.
La longueur du côté b correspond à la racine carrée de \(320 \ \mathrm{cm}^{2}\).
\(\sqrt{320} \ \mathrm{cm}^{2} \approx 17,9 \ \mathrm{cm}\)
La mesure manquante, soit la longueur du côté b, a une longueur d’environ 17,9 cm.
Représentation symbolique
Il s’agit d’un triangle rectangle, alors j’utilise le théorème de Pythagore pour déterminer la mesure manquante :
\(b^{2} + 16^{2} = 24^{2}\)
\(b^{2} + 256 \ \mathrm{cm}^{2} = 576 \ \mathrm{cm}^{2}\)
\(b^{2} + 256 \ \mathrm{cm}^{2} \ – \ 256 \ \mathrm{cm}^{2} = 576 \ \mathrm{cm}^{2} \ – \ 256 \ \mathrm{cm}^{2} \)
\(b^{2} = 320 \ \mathrm{cm}^{2}\)
\(b = \sqrt{320} \ \mathrm{cm}^{2}\)
\(b \approx 17,9 \ \mathrm{cm}\)
La mesure manquante, soit la base du triangle rectangle, a une longueur d’environ 17,9 cm.
Source : En avant, les maths!, 8e année, CM, Sens de l’espace, p. 5-6.
CONNAISSANCE : Théorème de Pythagore
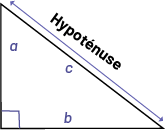Image Un triangle rectangle « a » « b » « c » dont l’angle droit « b » est en bas à gauche. Le côté
opposé à l’angle droit « c », est nommé hypoténuse.
Dans un triangle rectangle, la somme des carrés de la longueur des côtés formant l’angle droit est égale au carré de la longueur de l’hypoténuse.
\(a^{2} + b^{2} = c^{2}\)
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.