C2.1 Additionner des monômes du premier degré comprenant des nombres naturels à l’aide d’outils.
Habileté : additionner des monômes du premier degré comprenant des nombres naturels
Seuls les monômes du premier degré avec des variables semblables, comme 3m et 2m, peuvent être additionnés ou soustraits. Les représentations concrètes et visuelles sont essentielles pour favoriser la compréhension de ce concept.
On ne peut pas additionner des monômes n’ayant pas des variables semblables; par exemple, 5a + 10b ≠ 15ab.
Source : Programme-cadre de mathématiques, de la 1re à la 8e année, 2020, ministère de l’Éducation de l’Ontario.
Il est important que les élèves explorent l’addition de monômes à l’aide de différentes représentations afin de développer leur sens des opérations.
Voici quelques exemples :
- Représenter l’addition de monômes à l’aide de tuiles algébriques.
- Additionner à l’aide de cubes.
La valeur d’un cube est représentée par c.
Alors, la valeur de la structure ci-dessous équivaut à c + c + c + c = 4c.
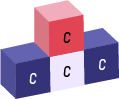
Si nous avons 5 structures comme celle illustrée ci-dessus, la valeur totale est de 4c + 4 c + 4c + 4c + 4c = 20c.
- Additionner à l’aide de la droite numérique.
Image Droite numérique de zéro à dix. Une accolade met en évidence 3 « x » plus accolade pour 5 « x », ÉGAL 8 « x ».
Une droite est divisée en 6 segments égaux. Chaque segment est nommé « m ». « m » plus, « m » plus, « m » plus, « m » plus, « m » plus, « m » plus égal 6 « m.
Puisque les monômes sont explorés pour la première fois en 6e année, il importe d’attribuer un contexte et un sens aux variables.
Connaissance : monômes du premier degré
Un monôme du premier degré comprend une variable à l’exposant 1; par exemple, dans le monôme 2m, l’exposant de m est 1. Lorsque l’exposant n’est pas mentionné, il est convenu qu’il s’agit de l’exposant 1.
Des exemples de monômes du deuxième degré sont x2 et xy. La raison pour laquelle xy est un monôme du deuxième degré est que x et y ont tous deux un exposant de 1. Le degré du monôme est déterminé par la somme de tous les exposants de ses variables.
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.