C2.3 Résoudre des équations qui comprennent des termes multiples, des nombres entiers et des nombres décimaux, dans divers contextes, et vérifier les solutions.
Habileté : résoudre des équations qui comprennent des termes multiples, des nombres entiers et des nombres décimaux
Dans Mettre l’accent sur le raisonnement algébrique M-12 (Ministère de l’Éducation de l’Ontario, 2013), il est expliqué que « […] de nombreux élèves ne reconnaissent pas que le signe égal indique une égalité » (p. 6), voire une équivalence entre deux expressions numériques. La « […] plupart des élèves ont interprété le symbole égal comme étant synonyme d’effectuer un calcul et [d’]inscrire la réponse après le symbole égal » (p. 6). Cette idée relève d’une association faite avec l’arithmétique où il est souvent demandé à l’apprenante ou à l’apprenant d’évaluer des équations ayant la forme suivante : a [signe d’opération] b = ?. De plus, l’utilisation de la calculatrice renforce cette idée, puisque la réponse est affichée lorsque l’élève appuie sur la touche =. Il est donc nécessaire de présenter aux élèves des situations arithmétiques qui leur demandent de vérifier si des égalités sont vraies ou fausses (par exemple, \(\ 14 + 3 = 16 + 1\)), ainsi que des égalités ayant des formes inhabituelles (\(\ 17 = 3 + 14\)). Pour faciliter le passage du raisonnement arithmétique au raisonnement algébrique, les élèves doivent développer certaines habiletés relatives aux relations entre des quantités.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 7e à la 10e année, p. 26.
Habileté à reconnaître une situation d’égalité
« Reconnaître une situation d’égalité, c’est identifier que deux quantités ont la même valeur » (Ministère de l’Éducation de l’Ontario, 2008 a, p. 75). L’utilisation de matériel concret et semi-concret pour représenter une égalité facilite le transfert aux égalités représentées à l’aide de symboles. Si les élèves sont habiles à utiliser des dispositions rectangulaires, alors reconnaître une situation d’égalité et la démontrer à l’aide d’expressions algébriques devient plus concret pour elles et pour eux.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 7e à la 10e année, p. 27.
Habileté à maintenir une situation d’égalité
Maintenir une situation d’égalité, c’est opérer sur les quantités pour s’assurer de préserver l’égalité. En explorant diverses situations, les élèves constatent que lorsqu’une quantité est ajoutée à un membre d’une égalité ou retirée de celui-ci, la même action doit s’effectuer sur l’autre membre de l’égalité. La balance à plateau permet de visualiser ces actions.
Exemple
| \(\ 2x + 6\ –\ 3x + 2\) Une grosse bille = x |
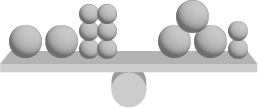
|
| Je retire 2 grosse billes de chaque côté de la balance, j’obtiens \(6 = x + 2\) |
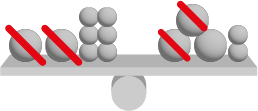
|
| Je retire 2 petites billes de chaque côté de la balance, j’obtiens \(4 = x\) |

|
Il est possible de résoudre l’équation de façon algébrique sans la représentation de la balance à plateau :
| \(\ 2x + 6 = 3x + 2\) | |
|---|---|
| \(\ 2x + 6 - 2x = 3x + 2 - 2x\) | J'enlève 2x de chaque côté du signe égal. |
| \(\ 6 - 2 = x + 2 - 2\) | J'enlève 2 de chaque côté du signe égal. |
| \(\ 4 = x\) | Je détermine la valeur de x. |
Résolution d’équations par inspection et à l’aide du modèle de la balance
 Description de la vidéo
Description de la vidéo
Description à venir
Résolution d’équations à l’aide d'un logigramme
 Description de la vidéo
Description de la vidéo
Description à venir
Comprendre le processus du maintien d’une situation d’égalité est une habileté très importante qui permet aux élèves de résoudre des équations à tous les cycles. Pour résoudre une équation ou vérifier si elle est vraie, il faut regrouper les variables d’un côté et les nombres de l’autre, tout en maintenant l’équilibre entre le membre de gauche et le membre de droite.
Exemple
| \(4(x - 5) + 2x = 3x + 7\) | |
|---|---|
| \(4x - 20 + 2x = 3x + 7\) | J'utilise la propriété de distributivité. |
| \(\displaylines{\begin{align} 4x + 2x - 20 + 20 &= 3x + 7 + 20 \\ 6x &= 3x + 27 \\ 6x - 3x &= 3x - 3x + 27 \\ 3x &= 27 \end{align}}\) | Je regroupe les variables d'un côté et les nombres de l'autre, tout en maintenant l'équilibre entre le membre de gauche et le membre de droite. |
| \(\frac{3x}{3} = \frac{27}{3}\) | Je divise chaque côté par 3. |
| x = 9 | Je détermine la valeur de x. |
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 7e à la 10e année, p. 30-31.
Il est bien de noter qu’il est avantageux dans la grande majorité du temps de simplifier le problème au fur et à mesure en regroupant les termes semblables et en effectuant des opérations de base sur les nombres.
Par exemple, si le problème est \(4x + 3x - 4 = 9x + 20 - 16 + (5x - 3x) \), il sera préférable de simplifier ce qui peut être simplifié dès le départ avant même d’annuler des termes de chaque côté du signe d’égalité (par exemple, soustraire 4x et 3x de chaque côté).
Habileté : vérifier les solutions à la suite de la résolution d’équations
Une fois que l’élève a résolu une équation, prendre l’habitude de vérifier sa solution en insérant cette valeur dans l’équation initiale est une excellente pratique à développer. L’élève doit tout simplement substituer la variable par cette valeur dans le membre de gauche (à gauche du signe d’égalité) et dans le membre de droite (à droite du signe d’égalité) puis identifier si la même réponse est obtenue de chaque côté.
Connaissance : équation
Relation d’égalité qui comporte une ou plusieurs variables.
\(\displaylines{\begin{align} ◊ + 3 &= 8 \mathord{\ ou} \\ 1 + ◊ + ◊ &= 11 \mathord{\ ou} \\ 3 \times ♣ &= 4 \times ▼ \times □\end{align}}\)
Source : Curriculum de l’Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l’Éducation de l’Ontario.
