D2.1 Utiliser le vocabulaire mathématique, y compris des termes comme « impossible », « possible » et « certain » pour exprimer la probabilité que des événements se produisent, et s’appuyer sur cette probabilité pour faire des prédictions et prendre des décisions éclairées.
Activité 1 : pas de danse (prédictions)
Matériel
- série de cartes numérotées de 1 à 10
- feuille de route de l’annexe 1.1 (une par élève)
- crayons
Sommaire
Dans cette activité, les élèves doivent prédire si, à la suite de déplacements choisis au hasard, elles et ils vont se trouver devant une ou un élève plus grand ou plus petit qu’elles et eux. Les élèves doivent aussi décrire, à l’aide des mots impossible, possible et certain, la probabilité de chaque événement.
Déroulement
Former des équipes de deux. Inviter les élèves à se placer debout en face de leur partenaire d’équipe de façon à former deux cercles, un cercle extérieur et un cercle intérieur. Expliquer que, tour à tour, les élèves dans un même cercle devront se déplacer vers leur droite en comptant le nombre de personnes correspondant au nombre indiqué sur une carte pigée au hasard.
Avant de procéder, remettre à chaque élève une feuille de route. Leur demander de prédire si, à la suite de chaque déplacement, elles et ils vont se trouver devant une ou un élève plus grand ou plus petit qu’elles et eux, et de noter cette prédiction en encerclant les mots plus grand ou plus petit sur la feuille de route. Leur demander également de choisir, parmi les mots impossible, possible, certain, celui qui décrit le mieux la certitude de leur prédiction.
Choisir une ou un élève du cercle extérieur et lui remettre une série de cartes numérotées de 1 à 10. Elle ou il pige une carte et les élèves qui font partie de ce cercle doivent se déplacer vers leur droite en comptant le nombre de personnes correspondant au nombre indiqué sur la carte pigée. Par exemple, si la carte pigée est le nombre 8, les élèves doivent se déplacer vers la droite et s’arrêter devant la ou le 8e élève. Les élèves vérifient alors si elles et ils font face à une ou à un élève plus grand ou plus petit qu’elles et eux et, si leur prédiction s’est réalisée, elles et ils font un crochet sur leur feuille de route à côté du mot Résultat; sinon, elles et ils n’écrivent rien.
L’élève qui a la série de cartes la remet ensuite à l’élève qui lui fait face dans l’autre cercle. C’est alors à son tour de piger une carte et au tour des élèves de ce cercle de se déplacer vers leur droite. L’activité se poursuit ainsi jusqu’à ce que chaque cercle d’élèves ait effectué cinq déplacements.
Lorsque l’activité est terminée, regrouper les élèves et leur demander de révéler leur prédiction ainsi que le nombre de fois que leur prédiction s’est réalisée. Animer une discussion en posant des questions telles que :
- Est-il possible pour une ou un élève de toujours s’arrêter devant une ou un élève plus grand? Pourquoi?
- Est-il possible pour une ou un élève de s’arrêter quelquefois devant une ou un élève plus petit? Pourquoi?
- Est-il possible que la prédiction d’une ou d’un élève se réalise toujours? Pourquoi?
- Est-il possible que la prédiction d’une ou d’un élève ne s’accomplisse jamais? Pourquoi?
- Est-il possible que deux élèves fassent la même prédiction, mais qu’elles et ils obtiennent des résultats différents? Pourquoi?
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 189-191.
Activité 2 : mon nombre chanceux (variabilité et hasard)
Matériel
- série de cartes numérotées de 1 à 10 (une par équipe de 2)
- sacs opaques (un par équipe de 2)
- feuille de papier
- crayons
Sommaire
Dans cette activité, les élèves effectuent une expérience simple afin de se conscientiser aux concepts de variabilité et de hasard.
Déroulement
Dire aux élèves que certaines personnes prétendent avoir un « nombre chanceux ». Leur demander si elles et ils ont un nombre chanceux et si oui, d’expliquer les raisons pour lesquelles elles et ils le considèrent comme tel. Leur proposer ensuite d’effectuer une expérience afin de découvrir si les nombres chanceux existent vraiment.
Former des équipes de deux. Remettre à chaque équipe un sac opaque et une série de cartes numérotées de 1 à 10. Inviter chaque élève à inscrire sur une feuille le nombre qui pourrait être son nombre chanceux. Leur demander de créer, sous ce nombre, un tableau de dénombrement comme dans l’exemple suivant.
| Nombre | Dénombrement |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
Demander aux équipes de placer les cartes dans le sac opaque et de bien les mélanger. Leur expliquer que chaque membre de l’équipe doit, à tour de rôle, piger une carte, indiquer le résultat à l’aide d’un crochet (√) dans la colonne Dénombrement de son tableau et remettre la carte dans le sac. Lorsque les élèves ont effectué un total de 20 tirages chacune et chacun, l’expérience s’arrête.
Lorsque toutes les équipes ont terminé, demander à quelques élèves de dire leur nombre chanceux et le nombre de fois qu’elle ou il l’a pigé lors des tirages.
Afin de faire ressortir l’idée que, dans une situation liée au hasard, les résultats sont variables et imprévisibles, poser des questions telles que :
- Avez-vous pigé plus souvent un nombre autre que votre nombre chanceux?
- Combien d’élèves ont pigé leur nombre chanceux plus souvent que n’importe quel autre nombre?
- Comment se fait-il que quelques élèves n’aient pas pigé leur nombre chanceux une seule fois?
- Pourquoi quelques élèves ont-elles et ont-ils pigé le nombre chanceux de leur partenaire et non le leur?
- Si vous refaisiez l’expérience, obtiendriez-vous les mêmes résultats? Pourquoi?
- Selon les résultats de cette expérience, y a-t-il un nombre qui est plus chanceux que les autres? Pourquoi?
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 191-193.
Activité 3 : concept du terme « certain »
Pour vérifier la compréhension des élèves du concept certain, le personnel enseignant demande d’abord à chaque élève d’indiquer le moyen qu’elle ou il préfère utiliser pour générer des résultats aléatoires. Les trois réponses les plus fréquentes sont : faire tourner l’aiguille d’une roulette, piger un objet d’un sac et lancer un dé.
Le personnel enseignant leur rappelle que, dans chacune de ces situations, on ne peut prédire avec certitude le résultat à moins, bien entendu, que les outils en question ne génèrent pas différents résultats de façon aléatoire. Il leur demande alors d’imaginer la façon dont chacun de ces outils pourrait être créé si on voulait être certain d’obtenir, par exemple, la lettre h comme résultat. Les élèves pourraient alors visualiser les outils de la façon suivante.
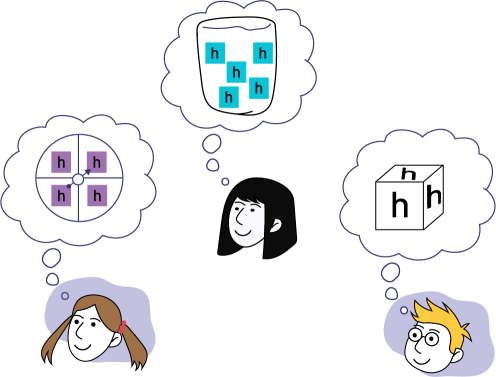
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 23.
ACTIVITÉ 4 : CONCEPT DES TERMES « IMPOSSIBLE », « POSSIBLE » ET « CERTAIN »
L’enseignante ou l’enseignant affiche au tableau les étiquettes impossible, possible et certain. Elle ou il présente aux élèves une série de fiches sur lesquelles un événement différent est inscrit (par exemple, « Ma grand-mère est sur la Lune. »; « Un chien mange une pomme. »). Elle ou il demande à chaque élève de choisir un événement et de le classer selon l’attribut. Pour représenter ce classement, l’élève doit se placer devant l’étiquette correspondant à la caractéristique choisie.
Sur la photo 1, on voit que la troisième élève à partir de la gauche comprend l’idée que le mot possible représente le continuum qui va de impossible à certain et qu’elle peut donc se placer plus près d’une extrémité de ce continuum que de l’autre.
 Photo de six élèves posant dans une salle de classe, devant un tableau vert où sont affichés les
mots Impossible, Possible et Certain. Trois élèves ont dans les mains des énoncés impossibles et se tiennent donc sous
l’affiche Impossible. Un élève a dans les mains un énoncé possible et se tient donc sous l’affiche Possible. Deux
élèves ont dans les mains des énoncés certains et se tiennent donc sous l’affiche Certain
Photo de six élèves posant dans une salle de classe, devant un tableau vert où sont affichés les
mots Impossible, Possible et Certain. Trois élèves ont dans les mains des énoncés impossibles et se tiennent donc sous
l’affiche Impossible. Un élève a dans les mains un énoncé possible et se tient donc sous l’affiche Possible. Deux
élèves ont dans les mains des énoncés certains et se tiennent donc sous l’affiche Certain
Photo 1
Le modèle de la ligne de certitude est un moyen visuel efficace pour représenter ce continuum.

Note : Comme illustré sur la photo 2, il peut être utile de commencer par demander aux élèves de classer un événement en fonction de seulement deux caractéristiques (par exemple, impossible et certain).

Photo 2
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 55-56.
Activité 5 : grand-maman tricote (exprimer la probabilité qu’un événement se produise)
Matériel
- panier
- pelotes de laine (une rouge, deux bleues, trois vertes)
- grand sac
- tableau collectif de dénombrement
Sommaire
Les élèves utilisent leur compréhension intuitive de la probabilité pour décrire, à l’aide du vocabulaire approprié, la probabilité de certains résultats d’une expérience simple.
Déroulement
Présenter aux élèves la situation suivante.
Grand-maman Dolorès désire tricoter un foulard pour garder son petit Jacob au chaud tout l’hiver. Son panier contient une pelote de laine rouge, deux pelotes de laine bleue et trois pelotes de laine verte. Comme elle n’arrive pas à décider la couleur de laine qu’elle va utiliser, elle décide de prendre au hasard une pelote dans le panier.
Présenter aux élèves un panier avec les six pelotes de laine. Leur demander de décrire, à l’aide des expressions possible, impossible ou certain, la probabilité que grand-maman Dolorès prenne une pelote de laine d’une couleur particulière et d’expliquer leur réponse.
Exemples de réponse possible
- C’est possible qu’elle prenne une pelote de laine verte, car il y en a plus de cette couleur que des autres couleurs.
- C’est impossible qu’elle prenne une pelote de laine blanche, car il n’y en a pas.
- C’est certain qu’elle prenne une pelote de laine rouge, bleue ou verte puisque ce sont les trois couleurs disponibles.
Note : Ces réponses montrent bien que la pensée probabiliste des élèves est encore à l’état embryonnaire. Il importe donc de les laisser s’exprimer sans accorder trop d’importance à la rigueur mathématique de l’argument présenté.
Proposer aux élèves d’effectuer une expérience. Placer les six pelotes de laine dans un sac. Demander aux élèves de venir, à tour de rôle, piger une pelote sans regarder à l’intérieur, puis de la remettre dans le sac. Inscrire le résultat au fur et à mesure dans un tableau de dénombrement.
Exemple
Couleur de la pelote de laine choisie
| Couleur | Dénombrement |
|---|---|
| Bleue | 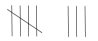 |
| Rouge | 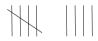 |
| Verte |  |
En tenant compte des résultats obtenus, poser des questions telles que :
- La pelote de laine rouge a été choisie plus souvent que la pelote de laine verte. Combien de fois de plus? (La pelote de laine rouge a été choisie cinq fois de plus que la pelote de laine verte.)
- Est-il certain que la pelote de laine rouge soit choisie le plus souvent? Pourquoi? (Non, car il y a qu’une seule pelote de laine rouge.)
- Puisqu’il y a plus de pelotes de laine verte, pourquoi n’est-il pas certain de la choisir? (Ce n’est pas la seule couleur disponible. Comme on ne pouvait pas voir ce que l’on pigeait, le hasard a décidé.)
Réaliser l’expérience de nouveau avec deux pelotes de laine de chaque couleur, puis comparer les résultats avec ceux de l’expérience précédente.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 225-227.
