D2.1 Use mathematical language, including the terms “impossible”, “possible”, and “certain”, to describe the likelihood of events happening, and use that likelihood to make predictions and informed decisions.
Activity 1: My Lucky Number (Variability and Chance)
Materials
- series of cards numbered from 1 to 10 (one per team of 2)
- opaque bags (one per team of 2)
- sheets of paper
- pencils
Summary
In this activity, students perform a simple experiment to become aware of the concepts of variability and chance.
Directions
Tell students that some people claim to have a "lucky number". Ask them if they have a lucky number and if so, to explain why they consider it lucky. Then suggest that they conduct an experiment to find out if lucky numbers really exist.
Form teams of two. Give each team an opaque bag and a set of cards numbered 1 to 10. Have each student write on a sheet of paper the number that could be their lucky number. Have them create a tally table underneath that number as in the following example.
| Number | Count |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 |
Have teams place the cards in the opaque bag and mix them well. Explain that each team member must take turns drawing a card, marking the result with a tally in the Count column of their table, and putting back the card in the bag. When students have completed a total of 20 draws each, the experiment ends.
When all teams have finished, ask a few students to say what is their lucky number and how many times they drew it.
To emphasize the idea that in a chance situation, outcomes are variable and unpredictable, ask questions such as:
- Did you pick a number other than your lucky number more often?
- How many students got their lucky number more often than any other number?
- Why did some students never pick their lucky number?
- Why did some students pick their partner's lucky number and not their own?
- If you did the experiment again, would you get the same results? Why?
- Based on the results of this experiment, is there a number that is luckier than the others? Why?
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Traitement des données et probabilité, p. 191-193.
Activity 2: Concept of the Term “Certain”
To test students' understanding of the concept of certainty, teachers first ask each student to indicate which way they prefer to generate random outcomes. The three most common responses are: spinning a spinner, drawing an object from a bag, and rolling a dice.
The teacher reminds them that in each of these situations, the outcome cannot be predicted with certainty unless, of course, the tools in question do not generate different outcomes randomly. The teacher then asks them to imagine how each of these tools could be created if they wanted to be certain of getting, for example, the letter h as an outcome.
Image Three character heads representing teachers: the first character thinks of a roulette wheel divided into four parts each with the letter "h", the second, a container that holds five "h’s ", and the third, a cube with the letter "h" on each side.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Traitement des données et probabilité, p. 23.
Activity 3: Concept of “Impossible”, “Possible” and “Certain”
The teacher posts the labels impossible, possible, and certain on the board. The teacher presents students with a series of index cards with a different event written on them (for example, "I know someone that lives on the moon."; "A dog eats an apple.") The teacher asks each student to choose an event and to describe the likelihood of this event happening. To represent this description, the student must stand in front of the corresponding label.
In photo 2, we see that in the bottom row, second student from the left, understands the idea that the word possible represents the continuum from impossible to certain , and therefore can stand closer to one end of that continuum than the other.
Image Photo of six students posing in a classroom, in front of a green chalkboard with the words Impossible, Possible, and Certain displayed on. Three students are holding impossible statements and are therefore standing under the “Impossible” sign. One student is holding a possible statement and is standing under the “Possible” sign. Two students are holding Certain statements and are standing under the “Certain” sign.
Photo 2
The probability line model is an effective visual way to represent this continuum.
Image Under the title "Probability Line", the word "possible" appears between two arrows pointing to the extremes of the progressive bar below. The bar starts with white and gradually turns dark blue. On the far left is the word "impossible", and on the far right is the word "certain".
Note: As illustrated in Photo 3, it may be helpful to begin by asking students to classify an event based on only two characteristics (for example, impossible and certain).
Photo 3
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Traitement des données et probabilité, p. 55-56.
Activity 4: Grandma Knits (Express the Probability of an Event Occuring)
Materials
- basket
- balls of wool (one red, two blue, three green)
- large bag
- group tally table
Summary
Students use their intuitive understanding of probability to describe, using appropriate vocabulary, the probability of certain outcomes of a simple experiment.
Directions
Present the following situation to the students.
Grandma Dolores wants to knit a scarf to keep little Jacob warm all winter long. Her basket contains one ball of red wool, two balls of blue wool and three balls of green wool. Since she can't decide which colour of wool to use, she decides to take a ball randomly from the basket.
Present students with a basket of six balls of wool and ask them to describe, using the terms possible, impossible or certain, the probability that Grandma Dolores will pick up a ball of wool of a particular colour and explain their answer.
Examples of possible answers
- It is possible that she will take a ball of green wool, because there are more of this colour than other colours.
- It is impossible for her to take a ball of white wool, because there is no white wool.
- It is certain that she will take a ball of red, blue or green wool since these are the three colours available.
Note: These responses show that students' probabilistic thinking is still in its beginnings, so it is important to let them express themselves without placing too much emphasis on the mathematical rigor of the argument presented.
Ask students to conduct an experiment. Place the six balls of wool in a bag. Ask students to take turns picking out a ball without looking inside, then putting it back in the bag. Record the results in a tally table.
Example
Colour of the Chosen Ball of Wool
| Colour | Count |
|---|---|
| Blue |  |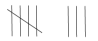
| Red |  |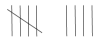
| Green |  |
Considering the results, ask questions such as:
- The red ball of wool was chosen more often than the green ball of wool. How many more times? (The red ball of wool was chosen five times more than the green ball of wool)
- Is it possible that the red ball of wool will always be chosen most often? Why? (No, because there is only one ball of red wool.)
- Since there are more balls of green wool, why won't green always be chosen? (It's not the only colour available. Since we couldn't see what we were picking, chance decided)
Perform the experiment again with two balls of wool of each colour, then compare the results with those of the previous experiment.
Source: translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Traitement des données et probabilité, p. 225-227.