D1. Littératie statistique :
Traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne.
Situation d’apprentissage : C’est oui ou c’est non?
Durée totale : environ 4 heures
Sommaire
Dans cette situation d’apprentissage, les élèves suivent le processus d’enquête pour réaliser un sondage auprès des élèves de la classe. Elles et ils doivent formuler une question d’intérêt concernant un seul élément d’information, effectuer une collecte de données, représenter ces données à l’aide d’un diagramme concret et interpréter les résultats.
| Attente | Contenus d'apprentissage |
|---|---|
| D1. Littératie statistique
Traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne. |
D1.2 Collecter des données au moyen d’observations, d’expériences et d’entrevues pour répondre à des questions d’intérêt concernant un seul élément d’information, enregistrer les données en utilisant des méthodes d’enregistrement de son choix, et organiser les données dans des tableaux de dénombrement. D1.3 Représenter des ensembles de données, en utilisant la correspondance un à un, à l’aide de diagrammes concrets et de diagrammes à pictogrammes comprenant des sources, des titres et des étiquettes appropriés. D1.5 Analyser divers ensembles de données présentées de différentes façons, y compris dans des tableaux de dénombrement, des diagrammes concrets et des diagrammes à pictogrammes, en se posant des questions au sujet des données, en y répondant et en tirant des conclusions, et ensuite formuler des arguments persuasifs et prendre des décisions éclairées. |
Intention pédagogique
Cette situation a pour but d’amener les élèves :
- à formuler une question d’intérêt concernant un seul élément d’information;
- à planifier et à effectuer une collecte de données;
- à passer d’une représentation personnelle des données à une représentation plus conventionnelle;
- à interpréter les résultats présentés dans un diagramme.
| Contexte pédagogique | Préalables |
|---|---|
|
La curiosité amène les jeunes enfants à se questionner et à questionner leur entourage afin de mieux comprendre le monde dans lequel elles et ils vivent. Ces jeunes arrivent donc à l’école avec une conception intuitive de questions simples qui n’exigent qu’un oui ou un non comme réponse. Au cycle préparatoire, les élèves ont eu l’occasion de trier et de classer des objets selon un attribut, de recueillir des données et de les représenter à l’aide de diagrammes concrets. La présente situation d’apprentissage permet aux élèves de continuer à développer ces habiletés en les initiant aux étapes du processus d’enquête. Elles et ils doivent effectuer un sondage, classer les résultats dans des catégories simples (par exemple, la catégorie oui et la catégorie non) et représenter ces données à l’aide d’un diagramme concret (par exemple, cubes rouges pour oui, cubes bleus pour non) et d’un diagramme avec illustrations. Elles et ils doivent également lire les données représentées par un diagramme (par exemple, nombre de oui et de non), les comparer (par exemple, il y a deux oui de plus que de non) et faire des inférences à partir de ces données. Grâce aux échanges mathématiques, la situation d’apprentissage permet aussi aux élèves de réaliser l’importance de respecter certains critères de construction de leur diagramme.
|
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent être capables :
|
Matériel
- photo de classe
- bandes de carton (une par équipe de deux)
- petits pince-notes ou trombones (deux par équipe de deux)
- cartons rigides pour les isoloirs (quantité correspondant à la moitié du nombre d’équipes)
- différents matériaux pour exprimer sa réponse au sondage, en quantité suffisante pour chaque équipe (par exemple, cubes, jetons, trombones, petits cartons, épingles à linge)
- matériel pour recueillir les réponses du sondage (par exemple, contenants, anneaux, lacets, ficelles)
- petites boîtes de carton (une par équipe de deux)
- listes des élèves de la classe et crayons (une par équipe de deux)
- grands cartons (un par équipe de deux)
- marqueurs (un par équipe de deux)
Vocabulaire mathématique
sondage, question d’intérêt, ensemble de données, collecte de données, tableau, résultat, titre, critères de classement, attribut, catégorie, fréquences, dénombrement, diagramme concret
Avant l’apprentissage (mise en train)
Durée : environ 20 minutes
Faire asseoir les élèves en demi-cercle et leur présenter une photo de classe. Si cela est possible, avoir plusieurs copies de cette photo (ou la numériser et la présenter à l’aide d’un tableau interactif) afin qu’elles et ils voient mieux les détails.
Animer une discussion en demandant aux élèves ce qu’elles et ils observent sur la photo. Voici des exemples d’observations possibles.
- Il y a quatre élèves qui portent des lunettes.
- André est le plus grand de la classe.
- Il y a sept élèves qui ont les cheveux blonds.
- Six élèves sont placés dans la première rangée, huit élèves dans la deuxième rangée et neuf élèves dans la dernière rangée.
- Il y a des élèves qui ont un motif sur leur chandail.
- Amid n’est pas sur la photo.
Laisser les élèves découvrir le plus de détails possible. Leur demander s’il y a quelque chose qu’elles et ils aimeraient connaître au sujet des autres élèves, mais qu’elles et ils ne voient pas sur la photo. Voici des exemples de réponses possibles.
- J’aimerais connaître le nombre d’élèves qui ont 6 ans.
- J’aimerais connaître la ville de naissance des élèves.
- J’aimerais connaître les élèves qui ont une sœur.
- J’aimerais connaître les élèves qui aiment le fromage.
- J’aimerais connaître le nombre de dents que chaque élève a perdues.
- J’aimerais connaître les élèves qui jouent au hockey.
Demander aux élèves ce qu’il faudrait faire pour obtenir de tels renseignements. Elles et ils répondront probablement qu’il faudrait poser des questions aux élèves de la classe. Si elles et ils n’utilisent pas le mot sondage, le présenter de façon informelle.
Le contenu des sections qui suivent est réparti selon les quatre étapes du processus d’enquête. Cette répartition est présentée à l’intention du personnel enseignant. En 1re année, il ne faut pas insister sur ces étapes auprès des élèves. C’est en passant naturellement d’une étape à l’autre dans le contexte de diverses enquêtes qu’elles et ils vont apprendre à les reconnaître.
Pendant l’apprentissage (exploration) – Étape 1
Durée : environ 15 minutes
Cerner la situation
Former des équipes de deux. Inviter les élèves à formuler une question au sujet d’un renseignement qu’elles et ils aimeraient obtenir à propos des élèves de la classe, et ce, de façon à pouvoir y répondre par oui ou par non.
Circuler et prêter attention aux discussions des élèves. Si des élèves s’attardent encore à ce qu’elles et ils voient sur la photo, leur rappeler qu’elles et ils doivent poser une question au sujet de ce qu’elles et ils ne voient pas sur la photo. Intervenir, au besoin, en posant des questions telles que :
- Que voulez-vous savoir?
- Peut-on répondre à votre question par un oui ou par un non? Sinon, comment pouvez-vous la modifier?
S’assurer que toutes les questions sont différentes les unes des autres. Les écrire au fur et à mesure au tableau ou sur un grand carton. Si deux questions sont identiques, inviter une équipe à en formuler une nouvelle. En profiter pour sélectionner les équipes qui présenteront leur question lors de l’échange mathématique. Dans la mesure du possible, choisir à la fois des équipes dont la question est bien formulée et d’autres dont la question n’est pas assez précise.
Après l’apprentissage (objectivation/échange mathématique) – Étape 1
Durée : environ 15 minutes
Inviter les équipes choisies à venir, à tour de rôle, présenter leur question oralement à la classe. Animer une discussion pour savoir si la question est bien formulée et s’il est facile d’y répondre à l’aide de oui ou de non. Le tableau ci-dessous présente des exemples de questions imprécises, accompagnées d’interventions possibles.
|
Questions imprécises |
Interventions possibles |
|
Est-ce que tu aimes la nourriture? |
Demander aux élèves s’il est possible de répondre par oui ou par non à cette question. Des élèves diront peut-être que cela dépend de la sorte de nourriture. Inciter les élèves à formuler une question plus précise. Par exemple : « Est-ce que tu aimes les carottes? » |
|
Est-ce que tu vas à la garderie après l’école? |
Demander aux élèves si cette question se répond par oui ou par non. Des élèves pourraient répondre qu’elles et ils vont à la garderie seulement deux jours par semaine. Amener les élèves à reformuler leur question de façon plus précise. Par exemple : « Est-ce que tu vas à la garderie tous les jours après l’école? » |
|
Est-ce que tu aimes les pommes rouges ou les pommes vertes? |
Demander aux élèves si elles et ils peuvent répondre par oui ou par non à cette question. Des élèves pourraient répondre qu’elles et ils aiment les pommes vertes, mais pas les pommes rouges. Alors, elles et ils ignorent si la question se répond par oui ou par non. Demander aux élèves de reformuler leur question en précisant un seul choix. Par exemple : « Est-ce que tu aimes les pommes rouges? » |
Demander aux équipes de réviser leur question et de la corriger au besoin. En profiter pour les sensibiliser à l’utilisation de la majuscule en début de phrase et du point d’interrogation à la fin. Remettre à chaque équipe une bande de carton et leur demander d’y écrire lisiblement leur question.
Pendant l’apprentissage (exploration) – Étape 2
Durée : environ 30 minutes
Discuter avec les élèves des différentes méthodes de collecte de données et du matériel qu’elles et ils pourraient utiliser pour effectuer leur sondage. Si les élèves ne semblent pas avoir d’idée, faire un rappel du matériel qu’elles et ils peuvent utiliser. Mettre ce matériel à leur disposition.
Inviter les membres de chaque équipe à choisir une méthode de collecte de données et à planifier la collecte. Circuler parmi les équipes et les inciter à réfléchir aux décisions à prendre en posant des questions telles que :
- Quel matériel comptez-vous utiliser pour effectuer votre sondage? (Dans la mesure du possible, faire en sorte que chaque équipe utilise un matériel différent.)
- Combien d’élèves répondront à la question?
- De quelle façon allez-vous utiliser ce matériel?
- De quelle quantité de ce matériel avez-vous besoin? Par exemple, dans une classe de 20 élèves, si une équipe utilise des jetons rouges pour oui et des jetons jaunes pour non, il leur faudra 20 jetons de chacune des couleurs, car il est possible que les élèves de la classe répondent à la question de la même façon. Cependant, si l’équipe utilise la même couleur pour les deux réponses, il leur faudra seulement 20 jetons de cette couleur.
Demander à chaque équipe de venir, à tour de rôle, chercher une boîte de carton, le matériel choisi pour le sondage, une copie de la liste des élèves de la classe et un crayon. Les élèves doivent ensuite placer le tout dans la boîte et chaque membre de l’équipe doit inscrire son prénom sur un côté de la boîte.
Faire une collecte de données
Durée : environ 60 minutes
Placer sur un pupitre un carton rigide de façon à former un isoloir. Expliquer aux élèves qu’elles et ils devront répondre à chacune des questions formulées par les diverses équipes en se plaçant derrière un isoloir comme si elles et ils étaient dans un bureau de vote. Leur expliquer le fonctionnement d’un bureau de vote, notamment le fait que toute personne doit s’identifier avant de voter et que son nom est alors rayé d’une liste.
Expliquer aux élèves la démarche à suivre pour procéder à la collecte de données. Voici une suggestion de démarche.
- Diriger la moitié des équipes vers une activité autonome (par exemple, lecture silencieuse, tâche individuelle). Inviter les autres équipes à placer un grand carton sur un pupitre de façon à former un isoloir, à y fixer leur question au moyen de petits pince-notes ou de trombones, et à placer leur matériel derrière le carton.
- Lorsque toutes ces équipes sont installées, demander à chaque membre de l’équipe de cocher son nom sur la liste de classe en mettant un crochet (√) ou une croix (X), et de répondre au sondage à l’aide du matériel.
- Leur expliquer ensuite la marche à suivre pour effectuer le sondage : une ou un membre de chaque équipe circulera d’un isoloir à l’autre pour répondre aux diverses questions pendant que l’autre restera près de l’isoloir pour lire, au besoin, la question à une ou à un élève qui éprouve des difficultés ou pour expliquer la façon d’utiliser le matériel. Ensuite, les deux membres de l’équipe changent de rôle.
- Leur préciser de ne pas oublier de cocher leur nom sur la liste avant de répondre, de lire attentivement la question affichée et d’attendre le signal avant de se rendre au prochain isoloir.
- S’assurer que l’ensemble des élèves comprennent bien la marche à suivre. Au besoin, montrer, avec une équipe, la façon d’effectuer la rotation (par exemple, l’ordre des nombres inscrits sur les cartons ou le sens des aiguilles d’une montre) et de répondre à la question.
- Lorsque les élèves ont terminé, demander aux équipes qui faisaient l’activité autonome de circuler à leur tour d’un isoloir à l’autre pour répondre aux questions. Pendant ce temps, les équipes qui ont rédigé les questions demeurent à leur isoloir pour assurer le bon déroulement du sondage.
- Lorsque l’ensemble des élèves ont répondu à la première série de sondages, s’assurer que les équipes placées près des isoloirs rangent soigneusement leur matériel dans un endroit prévu à cet effet sans modifier le choix de réponses. Ces réponses seront analysées ultérieurement.
- Reprendre ensuite la même démarche en inversant les rôles des équipes, c’est-à-dire que les équipes qui faisaient une activité autonome vont maintenant installer leur matériel dans un isoloir et vice versa.
Organiser les données (créer un diagramme)
Durée : environ 30 minutes
Une fois la collecte de données terminée, discuter en groupe-classe des moyens qui pourraient être utilisés pour présenter les résultats des divers sondages. Proposer aux élèves d’illustrer ces résultats en créant un diagramme à l’aide du matériel utilisé lors du sondage. Au besoin, leur présenter une photo d’un diagramme concret ou évoquer un diagramme qu’elles et ils ont déjà conçu. Reformer les mêmes équipes et remettre à chacune un grand carton. Leur demander de créer, à l’aide du matériel utilisé lors du sondage, un diagramme pour représenter les données recueillies.
À cette étape, il est important que les élèves puissent créer des représentations personnelles sans être dirigées et dirigés par le personnel enseignant afin que l’apprentissage lors de l’échange mathématique soit plus significatif.
Circuler et observer le travail des élèves. Au besoin, poser des questions telles que :
- Qu’est-ce qui représente les diverses catégories (par exemple, les blocs rouges représentent le nombre d’élèves ayant répondu le chien)?
- Comment les autres élèves sauront-elles et sauront-ils ce que représentent les diverses catégories?
- Comment sauront-elles et sauront-ils le nombre d’élèves qui ont choisi chaque catégorie?
- Comment sauront-elles et sauront-ils associer les résultats aux questions?
Observer les diagrammes produits par chacune des équipes et prévoir ceux qui seront présentés lors de l’échange mathématique. Afin d’aider les élèves à reconnaître l’importance de toutes les composantes d’un diagramme conventionnel, inclure dans votre choix quelques diagrammes qui peuvent être améliorés (par exemple, il manque le titre ou les catégories, les objets ne sont pas bien disposés horizontalement ou verticalement).
Après l’apprentissage (objectivation/échange mathématique) – Étape 2
Durée : environ 60 minutes
Lorsque toutes les équipes ont terminé, inviter les élèves à s’asseoir en demi-cercle. Demander aux équipes sélectionnées de présenter, tour à tour, leur diagramme aux autres élèves. Après chaque présentation, demander aux élèves qui ont présenté leurs résultats de la même façon de lever la main. Animer un échange de façon à faire ressortir les forces et les lacunes de chaque diagramme.
Les exemples ci-dessous ont été obtenus lors de la mise à l’essai de la situation d’apprentissage. Ils sont représentatifs du genre de difficultés que les élèves peuvent éprouver. Il revient au personnel enseignant d’adapter ses interventions en fonction des diagrammes produits par ses élèves.
| Observations possibles | Interventions possibles |
|---|---|
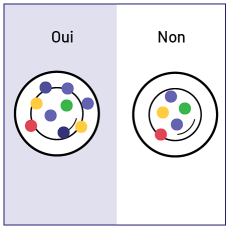
Les élèves disposent les jetons dans des contenants, identifient les catégories, mais ne forment ni colonnes ni rangées. |
Demander aux élèves comment leurs camarades pourront déterminer le nombre de résultats par catégorie. Leur demander s'il est facile, à première vue, de déterminer le nombre de oui. Les inciter à former des regroupements égaux de jetons dans chaque assiette. |
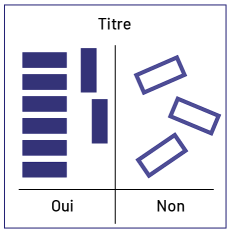
Les élèves forment plusieurs colonnes orientées différemment, et il y a trop d'espace. |
Demander aux élèves s'il est facile, à première vue, de déterminer le nombre de oui. Les inciter à placer les cartons dans chaque catégorie en une seule colonne, sans laisser d'espace entre eux. |
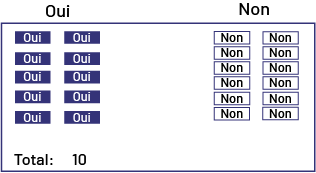
Les élèves écrivent le nom des catégories en haut du diagramme plutôt qu'en bas et disposent les cartons en deux colonnes au lieu d'une seule. |
Demander aux élèves s'ils peuvent déterminer, sans dénombrer, quelle catégorie contient le plus de cartons. Leur expliquer que pour mieux comparer les résultats, il est préférable de disposer les cartons dans chacune des catégories en une seule colonne et qu'il est plus facile de lire le diagramme lorsque le nom des catégories est placé au bas de chaque colonne. |
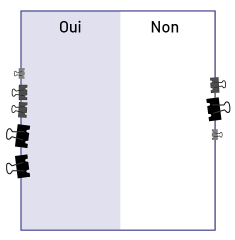
Les élèves utilisent des pince-notes de différente grandeur. |
Expliquer aux élèves que le diagramme pourrait nous induire en erreur puisque les différents pince-notes n'occupent pas tous le même espace. On ne peut donc pas se fier à la longueur de la colonne de pince-notes de chaque côté du carton pour déterminer s'il y a davantage de oui ou de non. |

Voyant qu'une catégorie contient trop de données pour l'espace disponible, les élèves forment deux colonnes. |
Demander aux élèves de trouver un moyen de placer tous les jetons dans une catégorie sans dédoubler la colonne (par exemple, ajouter un deuxième carton au haut du premier pour l'allonger et apposer le titre sur ce nouveau carton). Leur indiquer aussi qu'il serait préférable, pour être en mesure de comparer le nombre de jetons dans chaque colonne, de disposer les jetons l'un au-dessus de l'autre sans laisser d'espace entre eux. |
Au besoin, modeler la construction d’un diagramme avec du matériel représentatif. Tracer une ligne horizontale pour fixer le bas du diagramme (le point de départ des objets) en laissant suffisamment d’espace pour écrire le nom des catégories. Tracer une ligne verticale pour séparer les deux catégories comme sur les deux diagrammes ci-dessous. Expliquer que les premiers objets dans chaque catégorie doivent être déposés à la base du diagramme le long de la ligne horizontale et que les prochains objets doivent être placés par-dessus sans espace ni chevauchement (Diagramme A). Souligner que, s’il y a des espaces entre les objets (Diagramme B), il est difficile de comparer la longueur des bandes correspondant à chaque catégorie.
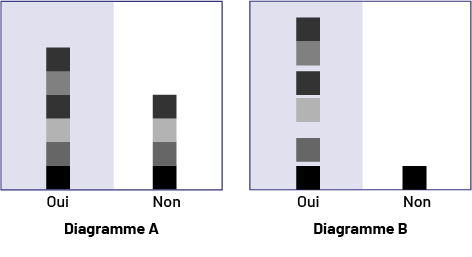
Expliquer aussi l’importance d’utiliser des objets de même grandeur. Si les objets ne sont pas tous de la même grandeur (par exemple, pince-notes de différentes grandeurs), leur conseiller de disposer côte à côte des papiers ou des cartons de mêmes dimensions de façon à former des colonnes ou des rangées, puis de déposer un objet sur chaque papier ou carton. Ainsi, les résultats seront présentés de façon organisée et il sera facile de comparer les quantités.
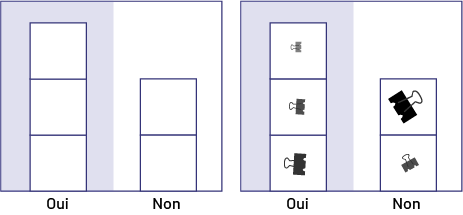
Enfin, préciser que si une colonne ou une rangée est plus longue que le carton, il est possible d’ajouter un deuxième carton. Pour cette raison, il est préférable de rédiger le titre à la fin.
Demander à quelques élèves de décrire dans leurs mots la procédure que vous avez modelée afin d’en dégager les éléments importants. Inviter chaque équipe à apporter, au besoin, des corrections à son diagramme de façon à tenir compte des observations faites lors de l’échange mathématique. Poursuivre l’objectivation en comparant les deux versions d’un même diagramme et en relevant les éléments qui font que la deuxième version est plus facile à interpréter.
Analyser les données et interpréter les résultats
Utiliser quelques-uns des diagrammes concrets créés par les élèves pour les inciter à analyser les données et à tirer des conclusions. Dans la mesure du possible, utiliser à la fois des diagrammes dont les données sont présentées en colonnes et des diagrammes dont les données sont présentées en rangées. Pour aider les élèves à développer les habiletés liées à l’interprétation des diagrammes, il est important de leur poser des questions de chacun des trois niveaux de compréhension.
- Lire les données (niveau 1)
- Est-ce que les composantes du diagramme sont toutes présentes? Pouvez-vous les montrer? (Oui. Notre titre, c’est la question que nous avons formulée. Nous avons pris des cubes rouges pour représenter les pommes rouges et des cubes verts pour les pommes vertes. Nous avons disposé nos cubes en colonnes et au bas, nous les avons indiquées.)
- Comment savez-vous que les réponses sont représentées? (Chaque colonne ou rangée est identifiée.)
- Est-il important que les colonnes ou les rangées aient le même point de départ? Pourquoi? (Oui, c’est important puisque cela nous permet de comparer les résultats dans chaque catégorie sans avoir à dénombrer tous les objets.)
- Que peut-on faire si les objets ne sont pas de la même grandeur? (On peut déposer les objets sur des papiers ou des cartons de dimensions identiques, puis les disposer côte à côte en colonnes ou en rangées.)
- Les espaces entre les objets doivent-ils être égaux? Pourquoi? (Oui. Si les espaces ne sont pas égaux, on pourrait penser à tort qu’une colonne est plus longue qu’une autre.)
- Combien y a-t-il de résultats oui et de résultats non?
- Qu’est-ce que ces résultats nous disent? (Ils nous disent que 14 élèves de la classe sont nées et nés au Canada et que 10 sont nées et nés dans un autre pays.)
- Établir des liens entre les données (niveau 2)
- En comparant les résultats dans chaque catégorie, quels renseignements pouvez-vous donner? Comment le savez-vous? (La majorité des élèves de la classe aiment le fromage. Je le sais parce que la colonne des oui est plus longue.)
- Combien de non y a-t-il de plus que de oui? Comment le savez-vous? (Il y a 4 non de plus que de oui. Pour le trouver, j’ai commencé à dénombrer les non à partir de la fin de la colonne des oui.)
- Lire au-delà des données (niveau 3)
- Si on posait la même question aux élèves de la classe de madame Maude, les résultats seraient-ils les mêmes? Pourquoi? (Ils pourraient être très différents parce que c’est possible que dans cette classe il y ait beaucoup plus d’élèves qui soient nées et nés ailleurs qu’au Canada.)
- Si on effectuait le sondage de nouveau à la fin de l’année scolaire, les résultats seraient-ils les mêmes? Pourquoi? (Cela dépend de la question. Par exemple, « Est-ce que tu as un frère? » pourrait engendrer une autre réponse, s’il y a eu une naissance dans la famille avant la fin de l’année scolaire.)
- Maintenant que tu as observé le diagramme, que peux-tu me dire au sujet des résultats de ton sondage? (Je suis étonnée ou étonné qu’autant d’élèves soient nées et nés dans un autre pays.)
- Est-ce qu’il y a quelque chose que ton diagramme ne t’a pas permis de savoir? (J’ignore le pays de naissance des élèves qui ne sont pas nées et nés au Canada.)
- Est-ce que ton sondage t’amène à te poser d’autres questions? Lesquelles? (J’aimerais faire un autre sondage pour savoir si plusieurs élèves sont nées et nés au Liban, comme moi.)
Prolongement – 1
Demander aux élèves la façon dont elles et ils pourraient présenter leur diagramme à leurs parents. Si les élèves suggèrent de prendre une photo, leur indiquer qu’il est parfois difficile de distinguer les détails sur une photo. Les amener à suggérer de reproduire les détails de leur tableau à l’aide d’illustrations de l’objet qu’elles et ils souhaitent représenter. Attirer leur attention sur les composantes du diagramme à reproduire. Inviter les élèves à former de nouveau les mêmes équipes. Remettre à chacune une grande feuille ou un grand carton et mettre à leur disposition le matériel nécessaire (par exemple, crayons de couleur, crayons-feutres, petits carrés de papier ou de cartons de même dimension).
La création d’un diagramme avec illustrations est une étape importante avant la présentation du diagramme à pictogrammes où les objets sont représentés de façon symbolique.
Circuler parmi les équipes et observer le travail des élèves. Intervenir, au besoin, en posant des questions telles que :
- Comment représenterez-vous les catégories oui et non?
- Qu’est-ce qui représente le oui? le non?
- Comment vous assurerez-vous que toutes les illustrations sont de la même grandeur?
- Comment placerez-vous chaque illustration? (Côte à côte, en rangée ou en colonne.)
- Comment vos parents sauront-ils ce que représente votre diagramme? (En lisant le titre.)
- Est-ce que vos deux diagrammes représentent les mêmes résultats? Comment le savez-vous? (Oui, puisque chaque objet correspond à une illustration.)
Dès que toutes les équipes ont terminé, inviter les élèves à s’asseoir en demi-cercle. Demander à quelques équipes de présenter leur diagramme et d’interpréter ce que leurs parents découvriront en l’observant. Suggérer aux autres élèves de bien vérifier que toutes les composantes du diagramme sont présentes. S’il en manque, leur demander de proposer des changements pour l’améliorer. Au besoin, demander aux élèves de corriger ou de modifier leur diagramme.
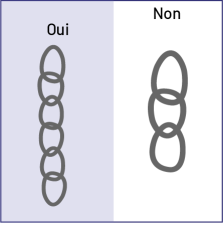
Les dessins des maillons du oui ne sont pas de la même grandeur que ceux du non, ce qui peut fausser l'interprétation.
De plus, les catégories sont indiquées au haut de la feuille et ne sont pas à la même hauteur.
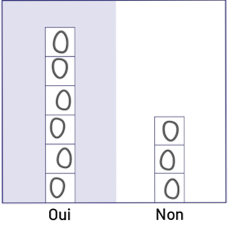
Après correction, les élèves ont utilisé des papillons autocollants identiques sur lesquels ils ont dessiné chaque maillon.
De plus, le nom des catégories et le point de départ sont situés au bas du diagramme.
Discuter avec les élèves des ressemblances et des différences entre un diagramme concret et un diagramme avec illustrations.
Prolongement – 2
Expliquer aux élèves qu’il existe des diagrammes qui représentent les objets par des symboles que l’on appelle des pictogrammes. Leur présenter des exemples de diagrammes contenant des pictogrammes (par exemple, 😀, ⭐). Leur montrer qu’il est nécessaire d’ajouter une légende pour expliquer le sens de chaque pictogramme. Leur demander de choisir un pictogramme qui pourrait remplacer les illustrations de leur diagramme.
Différenciation pédagogique
La situation d’apprentissage peut être modifiée pour répondre aux différents besoins des élèves.
|
Pour faciliter la tâche |
Pour enrichir la tâche |
|
|
Suivi à la maison
Proposer aux élèves de présenter à leurs parents leur diagramme avec illustrations et de leur expliquer les renseignements qu’elles et ils ont recueillis lors des sondages.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 151-168.
