D1.1 Trier et classer des ensembles de données portant sur des personnes ou des objets en fonction de deux attributs, en utilisant des tableaux et des logigrammes, y compris des diagrammes de Venn et de Carroll.
HABILETÉ : TRIER ET CLASSER DES ENSEMBLES DE DONNÉES
Trier consiste à grouper des objets qui présentent une caractéristique commune (par exemple, objets qui sont gros) et à écarter ceux qui ne la présentent pas (par exemple, objets qui ne sont pas gros).
Classer consiste à concevoir des catégories sous lesquelles il est possible de grouper des objets qui se différencient les uns des autres (par exemple, gros, moyen, petit), et à grouper ces objets en fonction de ces catégories.
Ces deux habiletés se développent presque simultanément. Le lien étroit qui existe entre le tri et le classement rend souvent ces deux habiletés difficiles à observer séparément. Pour faciliter cette observation, le personnel enseignant devrait choisir des problèmes contextualisés, faisant davantage appel soit au tri, soit au classement.
« Les jeunes élèves doivent classer des choses de différentes façons afin d’apprendre à interpréter des données portant sur le monde réel. L’objectif des activités sur les attributs est de développer un type de raisonnement flexible au sujet des caractéristiques des données. »
(Van de Walle et Lovin, 2007, p. 334)
Les habiletés à trier et à classer comprennent la capacité :
- à déterminer soi-même des classes à partir d’au moins un attribut;
- à grouper des objets adéquatement dans ces classes.
Pour trier et classer des objets, les élèves doivent d’abord, à partir de l’observation qu’elles et ils font de ces objets, être en mesure de choisir ceux qui présentent une caractéristique commune et écarter ceux qui ne la présentent pas. Les élèves peuvent également trier les objets qu’elles et ils ont écartés afin de les répartir dans d’autres classes. Il importe que les élèves aient l’occasion de trier et de classer les mêmes objets de diverses manières.
« En employant et, ou et non de façon appropriée, les élèves élargissent leurs schèmes de classification. »
(Van de Walle et Lovin, 2007, p. 336)
Une activité qui exige de définir des classes à l’aide du mot lien « ou » (par exemple, les triangles ou les carrés) est une activité complexe.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 36-37.
Représentations de tri et de classement
Au cours des premières expériences de tri et de classement, le personnel enseignant doit laisser les élèves utiliser des représentations personnelles (par exemple, matériel concret, dessin) avant de les exposer aux représentations à l’aide de diagrammes conventionnels (par exemple, diagramme de Venn, diagramme de Carroll). Par la suite, il doit leur fournir diverses occasions de choisir elles-mêmes et eux-mêmes le type de représentation qui se prête bien à ce qu’elles et ils veulent démontrer.
Représentations personnelles
De la maternelle à la 2e année, l’utilisation du matériel concret (par exemple, contenants, assiettes, grands cartons divisés en sections) facilite la représentation de tri et de classement d’objets.
Les habiletés développées au cours d’activités de tri et de classement d’objets concrets serviront lorsqu’il s’agira de définir des catégories qui permettront de regrouper des données obtenues dans le cadre d’une enquête et de créer un diagramme pour les représenter. Il importe cependant de souligner que le classement de données requiert des élèves un niveau d’abstraction plus élevé que le classement d’objets concrets. Le personnel enseignant peut les aider à acquérir ce niveau d’abstraction en leur suggérant d’abord de représenter le classement des réponses à une question de sondage à l’aide de matériel représentatif. Par exemple, les élèves pourraient représenter les réponses à la question « As-tu un chat? » en plaçant des autocollants dans la colonne appropriée d’un tableau simple. Soulignons que ce genre de tableau initie aussi les élèves au classement à l’aide d’un diagramme de Carroll.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 45-47.
CONNAISSANCE : ATTRIBUT
Un attribut d’un objet correspond à l’une de ses propriétés observables (par exemple, couleur, forme, grandeur).
Le concept d’attribut est très important puisqu’on le trouve et qu’on l’utilise dans tous les domaines en mathématiques. Lorsqu’il s’agit de trier et de classer, l’attribut d’un objet devient le critère de classement et les caractéristiques de l’attribut définissent les classes ou les catégories. Afin de classer, les élèves doivent :
- observer plusieurs attributs de l’objet (par exemple, couleur, matériau, grandeur);
- choisir un attribut pour le classement;
- relever certaines caractéristiques de cet attribut (par exemple, si l’attribut est le matériau, les caractéristiques peuvent être bois, plastique, papier).
Il est généralement plus facile de déterminer les caractéristiques d’un attribut que de définir l’attribut lui-même, car définir un attribut exige un effort de synthèse. Par exemple, si les élèves observent que les boutons sont lisses, rugueux ou ondulés, elles et ils utiliseront ces caractéristiques pour définir les trois classes dans lesquelles seront groupés les boutons. Après analyse, les élèves pourront reconnaître que ce sont là trois caractéristiques de l’attribut texture. Dans certains cas, il est préférable que le personnel enseignant propose au départ le choix d’un attribut.
Note : Les attributs permettent de trier et de classer des données en catégories, et les catégories permettent de créer des tableaux et des diagrammes.
Au fil des activités, les élèves prennent conscience que la description d’un ensemble doit être précise de sorte que l’on puisse déterminer avec certitude si tel ou tel objet appartient ou pas à la catégorie. Par exemple, les élèves réalisent que des catégories comme « gros, pas gros » ou « drôle, pas drôle » sont sujettes à la subjectivité de la personne qui effectue le classement.
Certaines descriptions d’objets se fondent sur la comparaison. Lorsque l’attribut correspond à une mesure (par exemple, longueur), les caractéristiques peuvent être définies à l’aide d’une comparaison (par exemple, objets plus longs que la craie).
Le tableau ci-dessous présente quelques exemples d’attributs et de caractéristiques que les élèves pourraient utiliser pour classer une collection de boutons.
| Attribut | Caractéristiques |
|---|---|
| texture | lisse, rugueux ou ondulé |
| nombre de trous | 0, 2, 3 ou 4 |
| grandeur | petit ou gros, long ou court |
| épaisseur | mince ou épais |
| forme | rond ou non rond |
| couleur | rouge, bleu, ou noir; brun ou non brun |
| vêtement auquel il correspond | pantalon, manteau ou chemise |
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 38-39.
Connaissance : caractéristique
Une caractéristique de l’attribut décrit comment l’attribut est reflété dans un objet particulier (par exemple, si l’attribut est la couleur, les caractéristiques peuvent être rouge, bleu, jaune).
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 38.
Connaissance : diagramme de Venn
Le diagramme de Venn met en évidence la réunion et l’intersection d’éléments de différents ensembles.
Le diagramme de Venn comprend les composantes suivantes :
- un titre qui désigne l’ensemble de référence;
- un rectangle qui regroupe l’ensemble de tous les objets à classer;
- un ou plusieurs cercles dans lesquels sont réunis les objets présentant une même caractéristique (le nombre de cercles dépend du nombre de catégories nécessaires au classement des objets);
- une étiquette qui définit chaque ensemble.
L’allure du diagramme de Venn peut varier selon la nature des catégories qu’il représente. Le diagramme A ci-dessous présente le classement d’objets selon une seule catégorie, soit « les enfants ». Ce type de diagramme peut être créé à l’aide de matériel concret dès la maternelle. On peut, par exemple, regrouper les noms ou les photos des enfants à l’intérieur d’une ligne fermée ou on peut demander aux enfants de se tenir debout à l’intérieur d’un cercle tracé sur le plancher. Dans un diagramme de Venn, tout objet qui fait partie de l’ensemble de référence peut être situé dans une des régions du diagramme, même les objets qui ne présentent pas une des caractéristiques retenues. Par exemple, dans le diagramme A, monsieur Paul n’est pas un élément de l’ensemble « les enfants », mais il fait partie de l’ensemble de référence « Les personnes dans la classe du jardin d’enfants ». Ce nom est alors placé dans la région à l’intérieur du rectangle, mais à l’extérieur du cercle.
Diagramme A
Le diagramme B ci-dessous représente le classement d’objets selon quatre catégories distinctes. Dans ce cas, il s’agit du classement d’aliments selon quatre groupes. Ce type de diagramme de Venn peut être créé à l’aide de matériel concret, de dessins ou d’illustrations dès la 1re année.
Diagramme B
Le diagramme C ci-dessous représente le classement d’objets selon deux catégories qui ne sont pas distinctes. Lorsqu’un objet peut être classé autant dans une catégorie que dans l’autre, il se trouve dans la région correspondant à l’intersection des deux cercles. Ce type de diagramme est la représentation la plus connue du diagramme de Venn; il peut être présenté dès la 2e année.
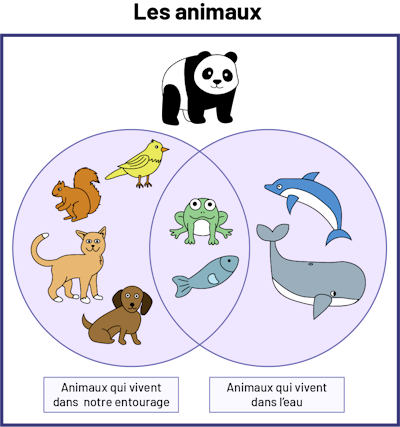Image
Diagramme de Venn C, dont le titre est Les animaux, formé de deux cercles : Animaux qui vivent dans notre entourage et
Animaux qui vivent dans l’eau. Le premier contient un chien, un chat, un écureuil et un oiseau, le second contient une
baleine et un dauphin, puis la zone du milieu contient un poisson et une grenouille.
Diagramme C
Dans ce diagramme, on note, par exemple, que :
- le chien est un élément de l’ensemble « Animaux qui vivent dans notre entourage »;
- la grenouille est à la fois un élément de l’ensemble « Animaux qui vivent dans notre entourage » et de l’ensemble « Animaux qui vivent dans l’eau »;
- le panda ne fait pas partie des ensembles « Animaux qui vivent dans notre entourage » et « Animaux qui vivent dans l’eau », mais il est un élément de l’ensemble de référence « Les animaux ».
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 48-51.
Connaissance : diagramme de Carroll
Le diagramme de Carroll met en évidence une partie de l’ensemble de référence et son complément.
Le diagramme de Carroll comprend les composantes suivantes :
- un titre qui désigne l’ensemble de référence;
- un rectangle divisé en régions représentant des sous-ensembles de l’ensemble de référence;
- des étiquettes pour désigner les sous-ensembles.
Le diagramme A ci-dessous représente le classement de souliers selon un seul attribut, soit les lacets. Les deux caractéristiques retenues de cet attribut sont « avec des lacets » et « sans lacets ». Notons que ces deux caractéristiques sont complémentaires, c’est-à-dire que tous les souliers possèdent l’une ou l’autre des caractéristiques, mais pas les deux.
Le diagramme B ci-dessous représente le classement de jetons numérotés selon la couleur (rouge ou vert) et la parité (pair ou impair).
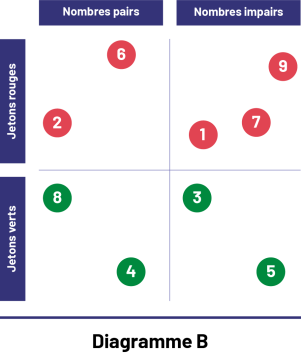Image Diagramme B composé de deux rangées et de deux colonnes.1re colonne : Nombres pairs1re rangée : Jetons rougesCette première case contient deux jetons rouges, l’un numéroté 6 et l’autre, 2.2e colonne : Nombres impairs1re rangée : Jetons rougesCette deuxième case contient trois jetons rouges, le premier numéroté 1, le deuxième, 7, et le troisième, 9.1re colonne : Nombres pairs2e rangée : Jetons vertsCette troisième case contient deux jetons verts, l’un numéroté 8 et l’autre, 4.2e colonne : Nombres impairs2e rangée : Jetons vertsCette troisième case contient deux jetons verts, l’un numéroté 3 et l’autre, 5.
Le diagramme C ci-dessous représente le classement de blocs logiques selon la couleur (bleu ou non bleu) et la forme (triangle ou pas un triangle).
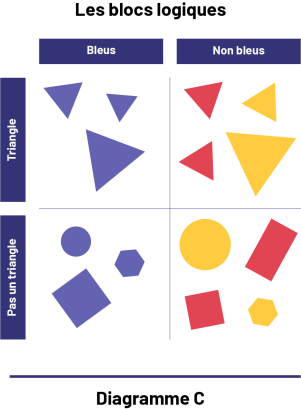Image
Diagramme C, dont le titre est Les blocs logiques, composé de deux rangées et de deux colonnes.1re colonne : Bleus1re
rangée : TriangleCette case contient trois triangles bleus.2e colonne : Non bleus1re rangée : TriangleCette case
contient deux triangles rouges et deux triangles jaunes.1re colonne : Bleus2e rangée : Pas un triangleCette case
contient un disque bleu, un carré bleu et un hexagone bleu.2e colonne : Non bleus2e rangée : Pas un triangleCette
contient un disque jaune, un hexagone jaune, un carré rouge et un rectangle rouge.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 52-53.