D1.3 Représenter des ensembles de données, en utilisant la correspondance un à plusieurs, à l’aide de diagrammes à pictogrammes et de diagrammes à bandes, comprenant des sources, des titres, des étiquettes et des échelles appropriés.
Activité 1 : à chaque tableau son diagramme (diagramme à pictogrammes et diagramme à bandes)
Matériel
Sommaire
Dans cette activité, les élèves associent un tableau de données à un diagramme à pictogrammes ou à un diagramme à bandes partiellement complété, puis ils ajoutent les composantes manquantes.
Déroulement
Grouper les élèves et remettre à chaque équipe une copie des annexes 3.3 et 3.4. Leur dire que chacun des quatre tableaux de données présentés à l’annexe 3.3 peut être représenté par deux des diagrammes partiellement complétés de l’annexe 3.4.
Expliquer aux élèves que le défi est de trouver quels deux diagrammes correspondent à chaque tableau de données. Pour ce faire, ils doivent lire attentivement les données dans les tableaux et voir quel diagramme partiellement complété peut représenter ces données. Au besoin, modeler une démarche possible à partir d’un des tableaux de données. Indiquer aux élèves que chaque équipe doit choisir un des quatre tableaux de données et trouver les deux diagrammes qui lui correspondent. Ils doivent ensuite compléter ces deux diagrammes en ajoutant les composantes manquantes (par exemple, titre, légende, échelle, catégories).
Circuler et observer afin de choisir, pour chacun des quatre tableaux, une équipe qui a trouvé les deux diagrammes correspondants et qui pourra présenter son travail lors de l’échange mathématique. Intervenir au besoin en posant des questions telles que :
- Pourquoi pensez-vous que ce diagramme correspond à ce tableau?
- Quel autre diagramme pourrait lui correspondre? Pourquoi?
- Comment avez-vous choisi l’échelle ou la légende?
- Quelles autres composantes devez-vous ajouter à ce diagramme?
Lorsque toutes les équipes ont terminé, demander tour à tour à chacune des quatre équipes identifiées préalablement d’indiquer quel tableau de données elles ont choisi, de présenter les deux diagrammes qui lui correspondent et d’expliquer comment elles ont fait pour le déterminer.
Après chaque présentation, demander aux autres élèves d’indiquer si toutes les composantes manquantes de ces deux diagrammes ont été ajoutées comme il se doit. Encourager les élèves à analyser et à interpréter les données dans les tableaux et les diagrammes.
Note : L’annexe 3.5 présente un exemple des huit diagrammes complétés.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 247-248.
Activité 2 : sautons à la corde (choisir le type de diagramme approprié)
Matériel
- cordes à sauter (1 corde par équipe de deux);
- grandes feuilles de papier (1 feuille par équipe de deux);
- marqueur de bingo;
- autocollant;
- crayons de couleur;
- règles;
- liste de classe (1).
Sommaire
Dans cette activité, les élèves choisissent le type de diagramme qui représente le mieux les différentes données recueillies.
Déroulement
La première partie de l’activité peut se dérouler dans le cadre de la période d’éducation physique. Grouper les élèves et distribuer une corde à sauter à chacune des équipes. Leur indiquer que chaque élève doit, à tour de rôle, sauter à la corde jusqu’à ce qu’il ou elle rate un saut et que l’autre membre de l’équipe doit compter les sauts effectués.
Dès le retour en classe, demander à chaque élève d’inscrire son résultat à côté de son nom sur la liste de classe. Remettre une copie de cette liste avec les résultats à chaque équipe, ainsi qu’une grande feuille. Indiquer aux élèves qu’ils doivent construire le diagramme de leur choix afin de représenter les données relatives au nombre de sauts à la corde réussis. Circuler et poser des questions telles que :
- Quel type de diagramme avez-vous choisi? Pourquoi?
- Comment allez-vous organiser vos données?
- Comment avez-vous désigné vos axes?
- Que signifie ce nombre sur votre axe horizontal?
- Pourquoi avez-vous utilisé cette échelle?
Inviter ensuite les équipes à présenter leur diagramme et à justifier certains de leurs choix (par exemple, choix de diagramme, de catégories, d’échelle). Au besoin, attirer l’attention des élèves sur les problèmes que certains diagrammes pourraient poser.
Exemple 1
Une équipe a utilisé les intervalles suivants pour organiser ses données : 0 à 5 sauts; 5 à 10 sauts; 10 à 15 sauts, etc. Leur demander d’expliquer dans quel intervalle ils ont placé la donnée correspondant à 5 sauts réussis; dans l’intervalle de 0 à 5 sauts ou dans celui de 5 à 10 sauts? Les inciter ensuite à créer des intervalles sans qu’il y ait de chevauchements.
Exemple 2
Une équipe a construit un diagramme à bandes dans lequel il y a une bande pour chaque nombre différent de sauts réussis. Faire remarquer qu’il est difficile d’interpréter un tel diagramme lorsque le nombre de bandes est élevé et que le fait de créer des classes selon un intervalle est un bon moyen de réduire ce nombre.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 250-251.
Activité 3 : diagramme à pictogrammes
Proposer la question d’intérêt ci-dessous aux élèves et les guider dans la collecte et la représentation des données.
| Question d'intérêt | Au lancer de deux dés, quelle somme représente le résultat le plus probable? |
| Type d'enquête | Enquête au moyen d'une expérience de probabilité |
| Type de renseignement recherché | Quantité |
| Regroupement des données | Catégories numériques |
| Représentation des données | Pictogrammes, selon une correspondance de un à un |
| Diagramme à pictogrammes |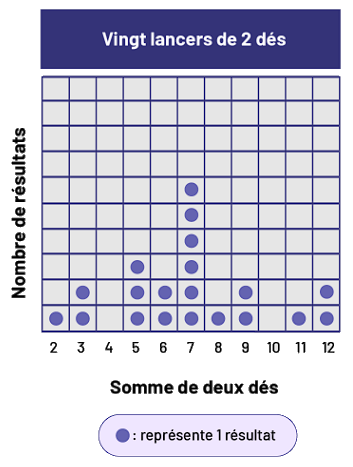 
Le tableau quadrillé s’intitule « Vingt lancers de deux dés ». L’axe horizontal se nomme
« Somme de deux dés » tandis que l’axe vertical se nomme « Nombre de résultats ». La somme deux obtient un
résultat, la somme 3 obtient deux résultats, la somme 4 n’obtient aucun résultat, la somme 5 obtient 3
résultats, la somme 6 obtient deux résultats, la somme 7 obtient 6 résultats, la somme 8 obtient un
résultat, la somme 9 obtient deux résultats, la somme dix n’obtient aucun résultat, la somme 11 obtient un
résultat et la somme 12 obtient deux résultats.
|
Exemples de questions :
- De quelle façon peut-on collecter les données? Par observation, par sondage, par expérience?
- Quel type de renseignements recherche-t-on?
- À l’aide de quel attribut seront formées les catégories? (données qualitatives ou données quantitatives)
- Quel type de diagramme représente mieux les données?
- Est-ce qu’un intervalle serait nécessaire pour les données quantitatives?
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 95.
Activité 4 : diagramme à pictogrammes
Proposer la question d’intérêt ci-dessous aux élèves et les guider dans la collecte et la représentation des données.
| Question d'intérêt | Quel est le fruit préféré des élèves de la classe? |
| Type d'enquête | Enquête au moyen d'un sondage |
| Type de renseignement recherché | Préférence |
| Regroupement des données | Catégories nominales |
| Représentation des données | Pictogrammes, selon une correspondance de un à deux |
| Diagramme à pictogrammes |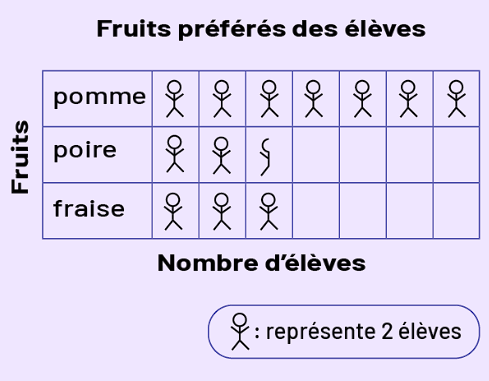 
Titre du tableau : Fruits préférés des élèves. Sous le tableau, il est écrit : « Nombre
d’élèves ». Trois fruits sont nommés : pomme, poire et fraise. Un bonhomme allumette représente deux élèves.
La pomme possède un bonhomme allumette, la poire possède deux bonshommes allumette et demi, et la fraise
possède 3 bonshommes allumette.
|
Exemples de questions :
- De quelle façon peut-on collecter les données? Par observation, par sondage, par expérience?
- Quel type de renseignements recherche-t-on?
- À l’aide de quel attribut seront formées les catégories? (données qualitatives ou données quantitatives)
- Quel type de diagramme représente mieux les données?
- Est-ce qu’un intervalle serait nécessaire pour les données quantitatives?
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 96.
Activité 5 : diagramme à bandes
Proposer la question d’intérêt ci-dessous aux élèves et les guider dans la collecte et la représentation des données.
| Question d'intérêt | Combien de minutes les élèves prennent-elles et prennent-ils pour se rendre à l'école à bicyclette à partir de la maison? |
| Type d'enquête | Enquête au moyen de mesures |
| Type de renseignement recherché | Grandeur |
| Regroupement des données | Intervalles de classe |
| Représentation des données | Bandes d'égales largeurs |
| Diagramme à band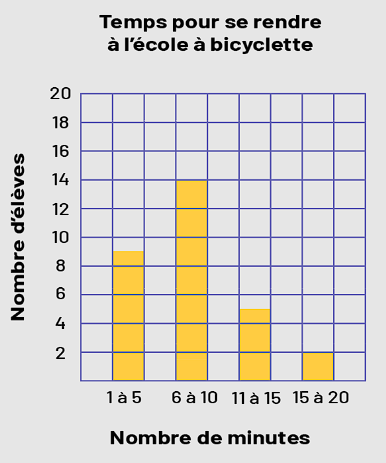es |  Un
diagramme quadrillé à 4 bandes jaunes illustre le temps pour se rendre à l’école à bicyclette. L’axe
horizontal concerne le nombre de minutes, et l’axe vertical concerne le nombre d’élèves. D’une à 5 minutes,
la bande indique 9 élèves. De 6 à 10 minutes, la bande indique 14 élèves. De 11 à 15 minutes, la bande
indique 5 élèves. Et de 15 à 20 minutes, la bande indique 2 élèves. |
Exemples de questions :
- De quelle façon peut-on collecter les données? Par observation, par sondage, par expérience?
- Quel type de renseignements recherche-t-on?
- À l’aide de quel attribut seront formées les catégories? (données qualitatives ou données quantitatives)
- Quel type de diagramme représente mieux les données?
- Est-ce qu’un intervalle serait nécessaire pour les données quantitatives?
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 97.
Activité 6 : réorganisons nos données
Présenter l’annexe 5.6 (Résultats d’une enquête). Inviter les élèves à interpréter les résultats en posant diverses questions telles que :
- Chez qui retrouve-t-on le même nombre de téléviseurs que chez vous? Le même nombre total de résidents à la maison? Le même nombre d’enfants?
- Y a-t-il des élèves qui partagent plus d’une caractéristique avec vous personnellement?
- Quel est le mode de chaque catégorie?
- Si nous faisions ce sondage auprès des élèves de notre classe, les résultats seraient-ils très différents? Pourquoi?
Sonder les élèves de la classe afin de déterminer, pour chacune des caractéristiques, le mode des données relatives à leur situation personnelle. Leur demander de comparer les données de la classe à celles de la classe de 5e année de l’école Tournesol.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 218.