D2.1 Utiliser le vocabulaire mathématique, y compris des termes comme « impossible », « peu probable », « équiprobable », « très probable » et « certain » pour exprimer la probabilité que des événements se produisent et s’appuyer sur cette probabilité pour faire des prédictions et prendre des décisions éclairées.
Activité 1 : agencement de vêtements (résultats possibles et probabilité)
Sommaire
Dans cette activité, les élèves énumèrent tous les résultats possibles d’une situation de probabilité et les utilisent pour décrire la probabilité de résultats particuliers.
Déroulement
Présenter la situation suivante aux élèves :
Olivier a une chemise rouge et un pantalon bleu qu’il désire mettre tous les jours pour aller à l’école. Sa mère aimerait bien qu’il porte aussi sa chemise jaune et sa chemise verte ainsi que son pantalon gris. Elle lui dit que dorénavant elle va placer ses trois chemises dans un sac opaque et ses deux pantalons dans un autre sac et que chaque matin, il devra retirer, sans regarder, une chemise du sac de chemises et un pantalon du sac de pantalons. Chaque soir, les vêtements portés au cours de la journée seront lavés et replacés dans les sacs afin que les mêmes vêtements soient disponibles chaque jour.
Demander aux élèves de déterminer tous les agencements possibles de chemise et de pantalon qu’Olivier pourrait porter. Si des élèves ont de la difficulté à les déterminer, mettre à leur disposition deux sacs avec des jetons de couleur pour représenter les vêtements. Ensuite, poser des questions telles que :
- Est-il possible qu’Olivier choisisse la chemise rouge et le pantalon bleu? Pourquoi?
- Est-il possible qu’Olivier choisisse la chemise rouge et le pantalon bleu chaque jour de la semaine? Pourquoi?
- Diriez-vous qu’il est peu probable, probable ou très probable qu’Olivier choisisse la chemise rouge et le pantalon bleu chaque jour de la semaine? Pourquoi?
- Est-il possible qu’Olivier choisisse un autre agencement que la chemise rouge et le pantalon bleu? Pourquoi?
- Diriez-vous qu’il est peu probable, probable ou très probable qu’Olivier choisisse un agencement autre que la chemise rouge et le pantalon bleu? Pourquoi?
- La mère d’Olivier décide d’ajouter un pantalon beige dans le sac contenant les pantalons. Est-ce que cette décision fait augmenter ou diminuer la probabilité qu’Olivier choisisse l’agencement qu’il préfère? Justifiez votre réponse.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 270-271.
Activité 2 : jaune ou vert? (prédictions)
Matériel
- sacs opaques contenant 3 jetons jaunes et 7 jetons verts (1 par équipe);
- crayons jaunes et crayons verts (1 de chaque couleur par équipe);
Sommaire
Dans cette activité, les élèves utilisent les résultats d’une expérience pour estimer le nombre de jetons jaunes et de jetons verts que contient un sac opaque.
Déroulement
Au préalable, préparer des sacs opaques contenant 3 jetons jaunes et 7 jetons verts. Grouper les élèves par deux et remettre un sac à chaque équipe en précisant de ne pas regarder dans le sac. Leur dire que le sac contient 10 jetons dont certains sont jaunes et d’autres sont verts. Expliquer aux élèves que l’activité consiste à tenter de déterminer, sans regarder dans le sac, combien de jetons sont jaunes et combien sont verts. Pour ce faire, elles et ils peuvent piger, à 10 reprises, un jeton du sac afin de noter sa couleur. Les élèves doivent cependant remettre le jeton dans le sac après chaque essai. Leur suggérer de consigner les résultats dans un tableau de leur choix.
Lorsque toutes les équipes ont terminé, demander à quelques-unes de présenter leur tableau et de dire combien elles estiment qu’il y a de jetons de chaque couleur dans le sac.
Exemple
Une équipe a noté les résultats suivants :

Les élèves indiquent alors que, selon elles et eux, il y a environ 5 jetons jaunes et 5 jetons verts dans le sac. Demander ensuite aux élèves de répéter l’expérience deux autres fois et d’utiliser les résultats pour estimer de nouveau la répartition des jetons de chaque couleur. Demander à d’autres équipes de présenter leur tableau et de dire combien elles estiment qu’il y a de jetons de chaque couleur dans le sac. Poser des questions telles que :
- Cette deuxième estimation est-elle pareille à la première que vous avez faite ou est-elle différente? Pourquoi?
- Puisque tous les sacs contiennent le même nombre de jetons jaunes et de jetons verts, pourquoi les équipes n’ont-elles pas toutes formulé la même estimation? (Parce que les estimations sont fondées sur des résultats qui relèvent du hasard.)
- Que pouvons-nous faire pour augmenter la probabilité que l’estimation corresponde à la répartition exacte de jetons de chaque couleur? (On pourrait répéter l’expérience un grand nombre de fois ou on pourrait regrouper les résultats des 30 tirages de chaque équipe.)
Demander à chaque équipe d’inscrire, dans un tableau préparé à cet effet, le nombre total de jetons jaunes et de jetons verts obtenus lors des 30 tirages. Faire le total pour chaque couleur et demander aux élèves d’utiliser ces nouvelles données pour formuler une troisième estimation de la répartition des jetons dans le sac. Leur demander de comparer le nombre de jetons de chaque couleur aux trois estimations afin de déterminer laquelle des estimations correspond le mieux à la répartition exacte.
En général, plus le nombre d’essais est grand, meilleure devrait être l’estimation. Par contre, en raison de la nature aléatoire des tirages, il se peut que, pour certaines équipes, ce ne soit pas le cas. C’est une occasion de discuter avec les élèves du concept de hasard.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 271-273.
Activité 3 : probabilité d’événements
Le personnel enseignant présente aux élèves la roulette illustrée ci-dessous et leur demande de classer chacun des résultats suivants selon l’attribut probabilité :
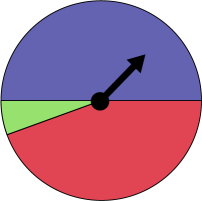 image Un diagramme circulaire muni d’une aiguille affiche une moitié
bleue, et l’autre moitié presque entièrement rouge sauf une petite section verte. L' aiguille pointe dans la section
bleue. À côté du diagramme, l’image d’une pointe de tarte bleue accompagne la mention : « L’aiguille s’arrête dans
un secteur bleu ». L’image d’une pointe jaune accompagne la mention : « L’aiguille s’arrête dans un secteur jaune ».
L’image d’une pointe verte accompagne la mention : « L’aiguille s’arrête dans un secteur vert ». L’image d’une
pointe mauve marquée d’un X rouge accompagne la mention : « L’aiguille s’arrête dans un secteur qui n’est pas mauve
». L’image d’une pointe rouge accompagne la mention : « L’aiguille s’arrête dans un secteur rouge ». Et l’image
d’une pointe verte marquée d’un X rouge accompagne la mention : « L’aiguille s’arrête dans un secteur qui n’est pas
vert »
image Un diagramme circulaire muni d’une aiguille affiche une moitié
bleue, et l’autre moitié presque entièrement rouge sauf une petite section verte. L' aiguille pointe dans la section
bleue. À côté du diagramme, l’image d’une pointe de tarte bleue accompagne la mention : « L’aiguille s’arrête dans
un secteur bleu ». L’image d’une pointe jaune accompagne la mention : « L’aiguille s’arrête dans un secteur jaune ».
L’image d’une pointe verte accompagne la mention : « L’aiguille s’arrête dans un secteur vert ». L’image d’une
pointe mauve marquée d’un X rouge accompagne la mention : « L’aiguille s’arrête dans un secteur qui n’est pas mauve
». L’image d’une pointe rouge accompagne la mention : « L’aiguille s’arrête dans un secteur rouge ». Et l’image
d’une pointe verte marquée d’un X rouge accompagne la mention : « L’aiguille s’arrête dans un secteur qui n’est pas
vert » 
Comme illustré ci-après, les élèves représentent ce classement en plaçant l’étiquette correspondant au résultat à un endroit approprié sur une ligne de probabilité.
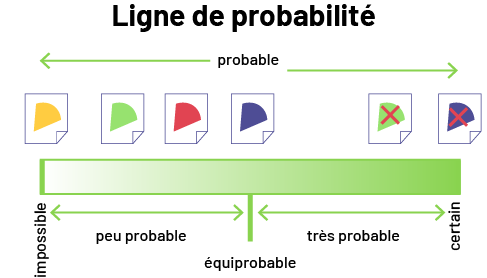 image
L’illustration a pour titre : Ligne de probabilité. Sous celui-ci, le mot « probable » possède à sa gauche une flèche
pointant à gauche, et à sa droite une flèche pointant à droite. En dessous, une barre progressive blanche devient
graduellement verte. À l’extrême-gauche de la barre, on trouve le mot « impossible », au-dessus duquel apparait la
pointe de tarte jaune. Sous la première moitié de la barre, il est écrit « peu probable », et l’on y associe la pointe
de tarte verte et la pointe de tarte rouge. En plein centre de la barre, on trouve le mot « équiprobable », auquel on
associe la pointe de tarte bleue. Sous la deuxième moitié de la barre, il est écrit « très probable », et on y associe
la pointe de tarte verte marquée d’un X rouge. Et au-dessus du mot « certain » à l’extrême-droite de la barre, on
trouve la pointe de tarte mauve marquée d’un X rouge.
image
L’illustration a pour titre : Ligne de probabilité. Sous celui-ci, le mot « probable » possède à sa gauche une flèche
pointant à gauche, et à sa droite une flèche pointant à droite. En dessous, une barre progressive blanche devient
graduellement verte. À l’extrême-gauche de la barre, on trouve le mot « impossible », au-dessus duquel apparait la
pointe de tarte jaune. Sous la première moitié de la barre, il est écrit « peu probable », et l’on y associe la pointe
de tarte verte et la pointe de tarte rouge. En plein centre de la barre, on trouve le mot « équiprobable », auquel on
associe la pointe de tarte bleue. Sous la deuxième moitié de la barre, il est écrit « très probable », et on y associe
la pointe de tarte verte marquée d’un X rouge. Et au-dessus du mot « certain » à l’extrême-droite de la barre, on
trouve la pointe de tarte mauve marquée d’un X rouge.
Il importe de souligner qu’aux cycles préparatoire et primaire, les élèves classent des événements ou des résultats d’une expérience de probabilité en se basant sur leurs expériences et sur leur intuition, et non à partir de connaissances théoriques du concept de probabilité. Ce classement intuitif dépend souvent de la compréhension qu’elles et ils ont des mots utilisés pour nommer les caractéristiques. Par exemple, si le personnel enseignant dit aux élèves qu’il est possible que la récréation soit prolongée de dix minutes, quelques élèves peuvent interpréter ceci comme voulant dire qu’il est certain qu’elle va l’être. Elles et ils ne comprennent pas qu’un événement qui est possible peut aussi bien se produire que ne pas se produire.
D’autres élèves ont de la difficulté à faire la distinction entre les caractéristiques jamais et impossible. Il leur est difficile de comprendre que même si un événement impossible est un événement qui ne peut jamais se produire, par contre, un événement qui ne s’est jamais produit n’est pas nécessairement impossible. À titre d’exemple, il est impossible que l’aiguille de la roulette dans l’exemple précédent s’arrête dans un secteur jaune. Donc, même si on la fait tourner 100 fois, elle ne s’arrêtera jamais dans un secteur jaune. Par contre, même si après 100 essais, l’aiguille ne s’est jamais arrêtée dans un secteur vert, cela ne veut pas nécessairement dire que ce résultat est impossible.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 57-58.
ACTIVITÉ 4 : COLLECTE DE DONNÉES RELIÉE AUX PROBABILITÉS
Dans le cadre d’une enquête au moyen d’une expérience de probabilité, une équipe fait tourner 15 fois l’aiguille d’une roulette et note, à l’aide d’un crochet (√), chaque résultat à l’endroit approprié dans un tableau.
.png) image Trois objets placés l’un en dessous de l’autre sont respectivement accompagnés de coches. Une
clé est accompagnée de 6 coches. Un trombone est accompagné de deux coches. Et une paire de ciseaux est accompagnée de
7 coches. À côté de ce tableau, il y a un cercle séparé en trois parties égales, lesquelles contiennent chacune l’un
des objets. Une flèche pointant à droite est placée sous la clé.
image Trois objets placés l’un en dessous de l’autre sont respectivement accompagnés de coches. Une
clé est accompagnée de 6 coches. Un trombone est accompagné de deux coches. Et une paire de ciseaux est accompagnée de
7 coches. À côté de ce tableau, il y a un cercle séparé en trois parties égales, lesquelles contiennent chacune l’un
des objets. Une flèche pointant à droite est placée sous la clé.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 72.
ACTIVITÉ 5 : ANALYSE DE DONNÉES LIÉES AUX PROBABILITÉS
Le personnel enseignant présente aux élèves un sac et leur indique qu’il contient un certain nombre de billes bleues (B), de billes rouges (R) et de billes jaunes (J). Il leur propose d’effectuer une enquête à l’aide d’une expérience de probabilité afin de déterminer s’il est probable, peu probable ou très probable que le sac contienne le même nombre de billes de chaque couleur. Le personnel enseignant groupe les élèves et demande à chaque équipe d’effectuer quatre tirages en s’assurant de remettre la bille dans le sac après chaque tirage. Les équipes inscrivent ensuite à tour de rôle leurs résultats dans un tableau collectif préparé à cet effet. Une fois rempli, le tableau présente l’ensemble des résultats obtenus par les équipes.
Source : Guide d’enseignement efficace des mathématiques de la maternelle à la 3e année, p. 76.
Les élèves se rendent compte que même si cette façon d’enregistrer les données est efficace, elle ne leur donne pas une bonne vue d’ensemble des résultats. Elles et ils décident donc de les regrouper dans un tableau de fréquences comme suit.
Billes pigées
| Équipe | 1er tirage | 2e tirage | 3e tirage | 4e tirage |
|---|---|---|---|---|
| 1 | B | B | R | J |
| 2 | B | R | J | B |
| 3 | B | J | B | R |
| 4 | R | J | B | B |
| 5 | B | B | B | J |
| 6 | R | B | J | B |
| 7 | J | B | B | R |
| 8 | J | B | R | B |
| 9 | J | R | B | B |
| 10 | B | R | J | R |
Résultats de quarante tirages d'une bille
| Résultat | Dénombrement | Fréquences |
|---|---|---|
| Bille bleue |  |
19 |
| Bille jaune |  |
10 |
| Bille rouge |  |
11 |
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 85.
Le personnel enseignant incite les élèves à analyser les données présentées dans ce tableau en posant des questions à chacun des trois niveaux de compréhension. Afin d’amener les élèves à lire les données, il pose des questions telles que :
- Quel est le titre du diagramme? (Résultats de quarante tirages d’une bille)
- Combien de fois a-t-on pigé une bille jaune? (Dix fois)
- En combien de catégories les résultats ont-ils été classés? (En trois catégories)
Afin d’amener les élèves à établir des liens entre les données, le personnel enseignant pose des questions telles que :
- Quel résultat a-t-on obtenu le plus souvent? (Le résultat « bille bleue »)
- Quel rapport y a-t-il entre la fréquence de ce résultat et la fréquence de chacun des deux autres résultats? (La fréquence du résultat « bille bleue » est à peu près le double de la fréquence de chacun des deux autres résultats. Elle est à peu près la même que les fréquences des résultats « bille rouge » et « bille jaune » combinés.)
Afin d’amener les élèves à lire au-delà des données, le personnel enseignant pose des questions telles que :
- Quelle conclusion peut-on tirer de ces résultats? (Il y a probablement plus de billes bleues que de billes rouges ou de billes jaunes dans le sac.)
- Si vous aviez à piger une seule bille du sac et que vous deviez prédire le résultat, que diriez-vous? Pourquoi? (Je prédirais que ce sera une bille bleue parce qu’il semble y avoir davantage de billes bleues dans le sac que de billes rouges ou jaunes. J’aurais donc de meilleures chances de prédire juste.)
Note : Un ou une élève pourrait répondre, par exemple, que la bille pigée sera rouge parce que c’est sa couleur préférée. Ce type de réponse est commun chez les élèves dont la pensée probabiliste n’est pas encore très développée.
- Si on faisait quarante nouveaux tirages, est-ce qu’on obtiendrait les mêmes résultats? » (On n’obtiendrait pas nécessairement les mêmes résultats puisqu’ils relèvent du hasard. Par contre, on peut s’attendre à ce que le résultat « bille bleue » soit encore celui dont la fréquence est la plus élevée.)
Après que les élèves ont analysé les données recueillies, le personnel enseignant les incite à interpréter les résultats en posant des questions telles que :
- Qu’est-ce qu’on voulait savoir au début de l’enquête? (On voulait savoir s’il est probable, peu probable ou très probable que le sac contienne le même nombre de billes de chaque couleur.)
- Avons-nous obtenu la réponse à cette question? (Oui. Selon les résultats obtenus après quarante tirages, il est peu probable que le sac contienne le même nombre de billes de chaque couleur.)
- Pouvons-nous être certains que cette conclusion est exacte? (Nous ne pouvons pas être certains parce que les résultats des tirages relèvent du hasard.)
- Que pourrions-nous faire pour augmenter la probabilité que cette conclusion soit exacte? (Nous pourrions reprendre l’expérience et effectuer, par exemple, cent tirages au lieu de quarante.)
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 107-109.
