La vue d'ensemble

À vue d'oeil...

Un remaniement des guides d'enseignement efficace en mathématiques

FrançaisEnglish

D1.1 Trier et classer des ensembles de données portant sur des personnes ou des objets en fonction de deux ou trois attributs, en utilisant des tableaux et des logigrammes, y compris des diagrammes de Venn et de Carroll, et des diagrammes en arbre.

HABILETÉ : TRIER DES ENSEMBLES DE DONNÉES

Trier consiste à grouper des objets qui présentent une caractéristique commune (par exemple, objets qui sont gros) et à écarter ceux qui ne la présentent pas (par exemple, objets qui ne sont pas gros).

Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 36.

HABILETÉ : CLASSER DES ENSEMBLES DE DONNÉES

Classer consiste à concevoir des catégories sous lesquelles il est possible de grouper des objets qui se différencient les uns des autres (par exemple, gros, moyen, petit), et à grouper ces objets en fonction de ces catégories.

Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 36.

CONNAISSANCE : ATTRIBUT

Un attribut d’un objet correspond à l’une de ses propriétés observables (par exemple, couleur, forme, grandeur).

Le concept d’attribut est très important puisqu’on le retrouve et qu’on l’utilise dans tous les domaines en mathématiques. Lorsqu’il s’agit de trier et de classer, l’attribut d’un objet devient le critère de classement et les caractéristiques de l’attribut définissent les classes ou les catégories. Afin de classer, les élèves doivent :

  • observer plusieurs attributs de l’objet (par exemple, couleur, matériau, grandeur);
  • choisir un attribut pour le classement;
  • identifier certaines caractéristiques de cet attribut (par exemple, si l’attribut est le matériau, les caractéristiques peuvent être bois, plastique, papier).

Il est généralement plus facile de déterminer les caractéristiques d’un attribut que de définir l’attribut lui-même, car définir un attribut exige un effort de synthèse. Par exemple, si les élèves observent que les boutons sont lisses, rugueux ou ondulés, ils utiliseront ces caractéristiques pour définir les trois classes dans lesquelles ils grouperont les boutons. Après analyse, ils pourront reconnaître que ce sont là trois caractéristiques de l’attribut texture. Dans certains cas, il est préférable que le personnel enseignant propose au départ le choix d’un attribut.

Note : Les attributs permettent de trier et de classer des données en catégories, et les catégories permettent de créer des tableaux et des diagrammes.

Au fil des activités, les élèves prennent conscience que la description d’un ensemble doit être précise de sorte que l’on puisse déterminer avec certitude si tel ou tel objet appartient ou pas à la catégorie. Par exemple, ils réalisent que des catégories comme « gros, pas gros » ou « drôle, pas drôle » sont sujettes à la subjectivité de la personne qui effectue le classement.

Certaines descriptions d’objets se fondent sur la comparaison. Lorsque l’attribut correspond à une mesure (par exemple, longueur), les caractéristiques peuvent être définies à l’aide d’une comparaison (par exemple, objets plus longs que la craie).

Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 38-39.

CONNAISSANCE : CARACTÉRISTIQUE

Une caractéristique de l’attribut décrit comment l’attribut est reflété dans un objet particulier (par exemple, si l’attribut est la couleur, les caractéristiques peuvent être rouge, bleu, jaune).

Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 38.

Connaissance : diagramme de Venn

Le diagramme de Venn met en évidence la réunion et l’intersection d’éléments de différents ensembles.

Le diagramme de Venn comprend les composantes suivantes :

  • un titre qui désigne l’ensemble de référence;
  • un rectangle qui regroupe l’ensemble de tous les objets à classer;
  • un ou plusieurs cercles dans lesquels sont réunis les objets présentant une même caractéristique (le nombre de cercles dépend du nombre de catégories nécessaires au classement des objets);
  • une étiquette qui définit chaque ensemble.

L’allure du diagramme de Venn peut varier selon la nature des catégories qu’il représente. Le diagramme A suivant présente le classement d’objets selon une seule catégorie, soit « les enfants ». Ce type de diagramme peut être construit à l’aide de matériel concret dès la maternelle. On peut, par exemple, regrouper les noms ou les photos des enfants à l’intérieur d’une ligne fermée ou on peut demander aux enfants de se tenir debout à l’intérieur d’un cercle tracé sur le plancher. Dans un diagramme de Venn, tout objet qui fait partie de l’ensemble de référence peut être situé dans une des régions du diagramme, même les objets qui ne présentent pas une des caractéristiques retenues. Par exemple, dans le diagramme A, Monsieur Paul n’est pas un élément de l’ensemble « les enfants », mais il fait partie de l’ensemble de référence « Les personnes dans la classe du jardin d’enfants ». Ce nom est alors placé dans la région à l’intérieur du rectangle, mais à l’extérieur du cercle.

Sur un tableau, un ensemble de prénoms est encerclé à l' aide d'un marqueur à tableau. Au-dessus de l’ensemble, il est écrit : « Les personnes dans la classe du jardin d’enfants. » En dessous de l’ensemble, il est écrit : « Les enfants ». À droite de l’ensemble, il est écrit : « Monsieur Paul ».Diagramme A

Le diagramme B suivant représente le classement d’objets selon quatre catégories distinctes. Dans ce cas, il s’agit du classement d’aliments selon quatre groupes. Ce type de diagramme de Venn peut être construit à l’aide de matériel concret, de dessins ou d’illustrations dès la 1re année.

Image Le diagramme B est une illustration ayant pour titre « Les groupes d’aliments », qui présente 4 images associées à leur groupe respectif. Le groupe Fruits et légumes est représenté par une tranche de melon d’eau, de la laitue, une banane et une carotte. Le groupe Produits céréaliers est représenté par deux pains et une tige de blé. Le groupe Lait et substituts est représenté par une pinte de lait, un yogourt à boire et un fromage. Le groupe Viandes et substituts est représenté par un poisson et un pilon de poulet.

Le diagramme C suivant représente le classement d’objets selon deux catégories qui ne sont pas distinctes. Lorsqu’un objet peut être classé autant dans une catégorie que dans l’autre, il se retrouve dans la région correspondant à l’intersection des deux cercles. Ce type de diagramme est la représentation la plus connue du diagramme de Venn; il peut être présenté dès la 2e année.

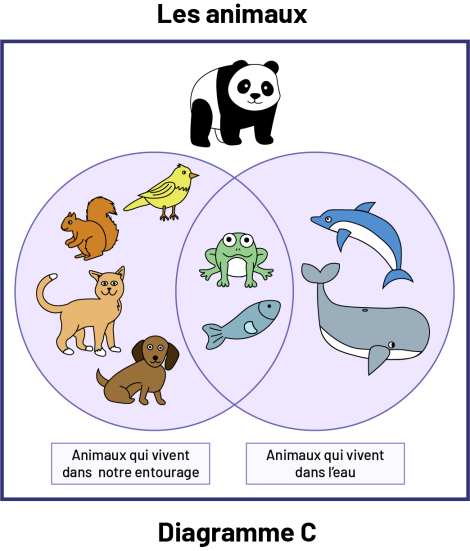Image Le Diagramme C a pour titre : Les animaux. Un panda est illustré au-dessus d’un diagramme de Venn à deux cercles. L’ensemble de gauche est nommé : « Animaux qui vivent dans notre entourage. » Il contient un oiseau, un écureuil, un chat et un chien. Il possède également une grenouille et un poisson dans sa partie partagée avec l' ensemble suivant. L’ensemble suivant se nomme « Animaux qui vivent dans l’eau ». En plus de la grenouille et du poisson qui sont partagés avec l’autre ensemble, cet ensemble contient un dauphin et une baleine.

Dans ce diagramme, on note, par exemple, que :

  • le chien est un élément de l’ensemble « Animaux qui vivent dans notre entourage »;
  • la grenouille est à la fois un élément de l’ensemble « Animaux qui vivent dans notre entourage » et de l’ensemble « Animaux qui vivent dans l’eau »;
  • le panda ne fait pas partie des ensembles « Animaux qui vivent dans notre entourage » et « Animaux qui vivent dans l’eau », mais il est un élément de l’ensemble de référence « Les animaux ».

Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 48-51.

Connaissance : diagramme de Carroll

Le diagramme de Carroll met en évidence une partie de l’ensemble de référence et son complément.

Le diagramme de Carroll comprend les composantes suivantes :

  • un titre qui désigne l’ensemble de référence;
  • un rectangle divisé en régions représentant des sous-ensembles de l’ensemble de référence;
  • des étiquettes pour désigner les sous-ensembles.

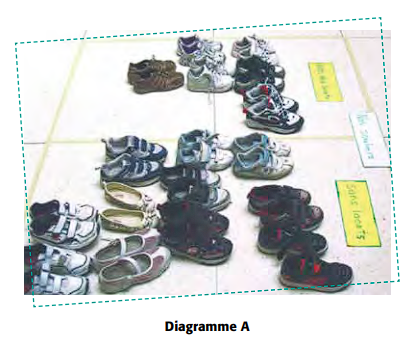
Le diagramme A suivant représente le classement de souliers selon un seul attribut, soit les lacets. Les deux caractéristiques retenues de cet attribut sont « avec des lacets » et « sans lacets ». Notons que ces deux caractéristiques sont complémentaires, c’est-à-dire que tous les souliers possèdent l’une ou l’autre des caractéristiques, mais pas les deux.

Le diagramme A est un diagramme de Caroll élaboré avec de vrais objets. Il a pour titre : « Nos souliers ». L’ensemble de gauche s’intitule « Avec des lacets » et présente 6 paires de chaussures qui s’attachent à l’aide de lacets. L’ensemble de droite s’intitule « Sans lacets » et présente 11 paires de chaussures qui s’attachent à l’aide de velcros, d’oeillets, ou qui sont dépourvus d’attaches.

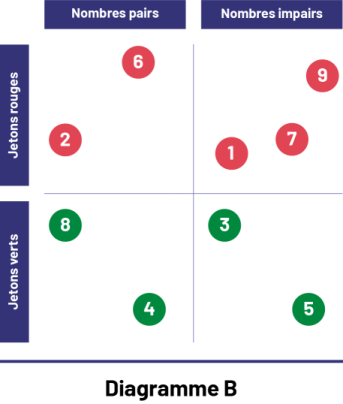
Le diagramme B suivant représente le classement de jetons numérotés selon la couleur (rouge ou vert) et la parité (pair ou impair).

Le Diagramme B présente 4 quadrants. Le quadrant en haut à gauche, « Nombres pairs » et « Jetons rouges », contient les jetons 2 et 6, qui sont rouges. Le quadrant en haut à droite, « Nombres impairs » et « Jetons rouges », contient les jetons un, 7 et 9, qui sont rouges. Le quadrant en bas à gauche, « Nombres pairs » et « Jetons verts », contient les jetons 4 et 8, qui sont verts. Et le quadrant en bas à droite, « Nombres impairs » et « Jetons verts », contient les jetons 3 et 5, qui sont verts.

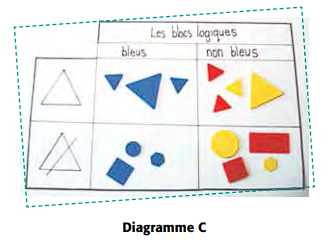
Le diagramme C suivant représente le classement de blocs logiques selon la couleur (bleu ou non bleu) et la forme (triangle ou pas un triangle).

Le Diagramme C présente 4 quadrants. Le quadrant en haut à gauche, « Bleus » et « Triangle » contient 3 triangles bleus de taille différente. Le quadrant en haut à droite, « Non bleus » et « Triangle », contient 2 triangles jaunes et 2 triangles rouges. Le quadrant en bas à gauche, « Bleus » et « Non triangle » contient un carré, un cercle et un hexagone bleus. Et le quadrant en bas à droite, « Non bleus » et « Non triangle » contient un cercle et un hexagone jaunes, et un carré et un rectangle rouges.

Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 52-53.

CONNAISSANCE : DIAGRAMME EN ARBRE

Un diagramme en arbre peut servir à déterminer toutes les combinaisons de catégories possibles pour les attributs associés à un ensemble de données en vue de déterminer les catégories pour la collecte de données.

On peut déterminer le nombre de combinaisons possibles en multipliant le nombre de catégories d’un attribut par le nombre de catégories des autres attributs. Prenons, à titre d’exemple, les attributs suivants : « forme » (cercle, rectangle, triangle, hexagone), « couleur » (rouge, bleu, vert) et « taille » (grand, pas grand). Dans cet exemple, le résultat de la multiplication 4 × 3 × 2 donne le nombre de combinaisons possibles.

Exemple

Diagramme en arbre à trois attributs

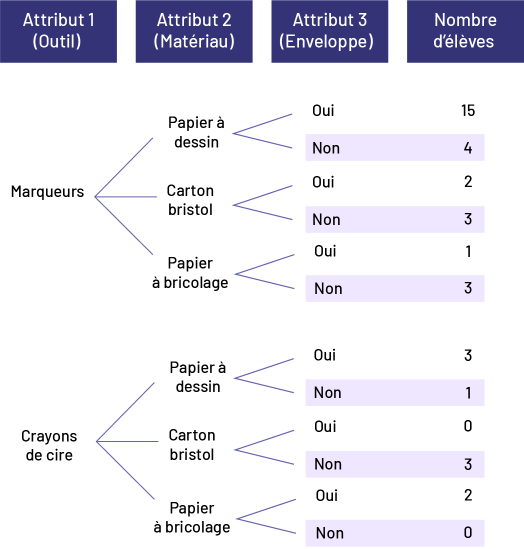
  • Les élèves de l’école B se sont fait poser une autre question, à savoir si elles et ils veulent une enveloppe pour leur carte. Le diagramme en arbre ci-dessous montre les réponses des élèves selon leur sélection de marqueurs ou de crayons de cire.
image L’attribut 1, l’outil, présente deux options : marqueurs ou crayons de cire. L’attribut deux, le matériau, présente 3 options : papier à dessin, carton bristol ou papier à bricolage. L’attribut 3, l’enveloppe, présente deux options : oui ou non. Et le nombre d’élèves varie de zéro à 15. Lorsque l' outil marqueurs est lié à papier à dessin et à oui, le nombre d’élèves est de 15. Lorsque l’outil marqueurs est lié à papier à dessin et à non, le nombre d’élèves est de 4. Lorsque l’outil marqueurs est lié au carton bristol et à oui, le nombre d’élèves est de deux. Lorsque l’outil marqueurs est lié à carton bristol et à non, le nombre d’élèves est de 3. Lorsque l’outil marqueurs est lié à papier à bricolage et à oui, le nombre d’élèves est d’un. Lorsque l’outil marqueurs est lié à papier à bricolage et à non, le nombre d’élèves est de trois. Lorsque l’outil crayons de cire est lié à papier à dessin et à oui, le nombre d’élèves est de 3. Lorsque l’outil crayons de cire est lié à papier à dessin et à non, le nombre d’élèves est d’un. Lorsque l’outil crayons de cire est lié à carton bristol et à oui, le nombre d’élèves est de zéro. Lorsque l’outil crayons de cire est lié à carton bristol et à non, le nombre d’élèves est de trois. Lorsque l’outil crayons de cire est lié à papier à bricolage et à oui, le nombre d’élèves est de 2. Et lorsque l’outil crayons de cire est lié à papier à bricolage et à non, le nombre d’élèves est de zéro.

Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.