D1.3 Représenter des ensembles de données, en utilisant la correspondance un à plusieurs, à l’aide de diagrammes à pictogrammes et de diagrammes à bandes, comprenant des sources, des titres, des étiquettes et des échelles appropriés.
HABILETÉ : REPRÉSENTER DES ENSEMBLES DE DONNÉES
Une fois que les données relatives à une enquête ont été regroupées par catégories dans un tableau de fréquences ou autre, il est souvent très utile de les représenter à l’aide d’un diagramme en raison de son impact visuel. En effet, un diagramme :
- présente l’information de façon organisée;
- est généralement plus facile à lire et à interpréter qu’une représentation de données à l’aide d’un texte ou d’un tableau;
- permet de voir l’ensemble des données en un coup d’œil et de s’en faire une première impression (par exemple, si les données sont réparties également ou inégalement entre les catégories);
- facilite la prochaine étape du processus d’enquête, soit l’analyse des données et l’interprétation des résultats.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 86.
Par exemple, les élèves peuvent représenter un ensemble de données statistiques de façon beaucoup plus succincte et efficace à l’aide d’un tableau ou d’un diagramme qu’à l’aide d’une description orale. Ils doivent cependant apprendre à utiliser correctement les diverses représentations conventionnelles des données (par exemple, tableau de fréquences, diagramme à pictogrammes, diagramme à bandes) afin de s’assurer que le message transmis est le bon et qu’il est bien compris par les autres. Elles et ils peuvent ensuite utiliser ces représentations pour justifier un raisonnement ou appuyer un argument lors d’un échange mathématique avec le groupe classe.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 30.
La représentation de données dans des tableaux et des diagrammes permet de communiquer des renseignements en vue de leur interprétation.
Les élèves doivent déterminer la meilleure façon de regrouper les données recueillies afin de faciliter leur analyse. Par la suite, elles et ils doivent choisir un mode de représentation approprié et le construire de façon à s’assurer de la clarté du message transmis.
Une fois que les données ont été recueillies et enregistrées, les élèves doivent les regrouper à l’intérieur d’un nombre restreint de catégories. Il n’y a pas de règle qui dicte la façon de regrouper les données. Le choix du regroupement dépend en grande partie de la sorte de données recueillies.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 80-81.
Les sources, les titres, les étiquettes et les échelles fournissent des précisions importantes sur les données d’un diagramme, incluant :
- La source indique l’origine des données recueillies.
- Le titre présente les données du diagramme.
- Les étiquettes indiquent les catégories ayant servi au classement des données.
- Les échelles indiquent les valeurs sur un axe du diagramme.
L’ordre des catégories est important dans les diagrammes présentant des données quantitatives. Les nombres sont placés en ordre croissant. En revanche, l’ordre des catégories importe peu dans les diagrammes présentant des données qualitatives (par exemple, les couleurs peuvent être placées dans n’importe quel ordre).
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : TYPES DE DIAGRAMME
Ligne de dénombrement
La ligne de dénombrement est utile pour représenter un grand nombre de données numériques. Chaque donnée est représentée par un X et les X correspondant à une même quantité sont disposés l’un au-dessus de l’autre de manière à former des colonnes. Puisque la hauteur de chaque colonne correspond alors à la taille de la fréquence qu’elle représente, l’analyse des données s’effectue facilement.
Exemple
Le personnel enseignant demande à ses élèves de vérifier depuis combien d’années leurs parents demeurent dans leur logis actuel. Les résultats sont représentés par la ligne de dénombrement suivante.
Image
La ligne de dénombrement s’intitule : « Nombre d’années que les parents des élèves de quatrième année habitent leur
logis actuel ». La ligne intitulée « Nombre d’années » est graduée de 1 à 23. Le chiffre 1 affiche la présence d’un X.
Le chiffre deux ne présente aucun X. Le chiffre 3 présente 4 X. Le chiffre 4 présente 6 X. Le chiffre 5 présente 5 X.
Les chiffres 6 et 7 ne présentent aucun X. Le chiffre 8 présente deux X. Les nombres 9, dix et 11 ne présentent aucun
X. Le nombre 12 présente un X. Le nombre 13 présente 7 X. Le nombre 14 présente 4 X. Le nombre 15 présente 5 X. Les
nombres 16, 17, 18 et 19 ne présentent aucun X. Le nombre 20 présente deux X. Les nombres 21 et 22 ne présentent aucun
X. Le nombre 23 présente un X.
On voit facilement d’après la répartition des X, qu’il y a eu deux vagues de déménagements, soit il y a de 3 à 5 ans et de 13 à 15 ans, ce qui pourrait être le résultat de la construction de nouveaux logis ou de la création de nouveaux emplois dans la ville.
Caractéristiques d’une ligne de dénombrement :
- Elle a un titre.
- Elle a un axe horizontal gradué portant une étiquette.
- Chaque donnée est représentée par un X. Les X qui représentent une même donnée numérique sont superposés et sont séparés l’un de l’autre par un espace constant.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 83-84.
CONNAISSANCE : DIAGRAMME À PICTOGRAMMES
Un diagramme à pictogrammes est semblable au diagramme à bandes sauf qu’on utilise des pictogrammes pour former les bandes. Ce type de diagramme n’est pas utilisé seulement au cycle primaire; il est aussi utilisé dans les journaux et les revues.
Un pictogramme est un dessin ou une image figurative. C’est pourquoi le diagramme à pictogrammes porte parfois le nom de diagramme figuratif.
Le choix du pictogramme a une certaine importance. Idéalement, le pictogramme devrait évoquer les données qu’il représente. De plus, il est généralement utile de choisir un pictogramme qui est facile à dessiner ou à recopier et facile à découper en demis ou en quarts.
Image
Le diagramme à pictogrammes s’intitule : « Nombre de biscuits vendus pendant la vente de pâtisseries ». L’axe
horizontal est nommé « Nombre de biscuits vendus » et l’axe vertical est nommé « Année d’études ». La légende indique
que chaque pictogramme de biscuit équivaut à 4 biscuits vendus. La deuxième année affiche 5 biscuits. La troisième
année affiche 3 biscuits. La quatrième année affiche 5 biscuits et un quart. La cinquième année affiche 3 biscuits et
trois quarts. La sixième année affiche 7 biscuits et demi.
Caractéristiques d’un diagramme à pictogrammes :
- Il a un titre.
- Il a un axe qui indique les catégories.
- Les deux axes ont chacun une étiquette.
- Il utilise un pictogramme répété pour représenter, à l’horizontale ou à la verticale, le nombre de données de chaque catégorie.
- L’espacement entre les pictogrammes est constant.
- Il a une légende qui indique ce que le pictogramme représente.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 82-83.
CONNAISSANCE : DIAGRAMME À BANDES
Le diagramme à bandes sert à représenter les fréquences d’un ensemble de données. Il est composé de bandes rectangulaires dont la longueur correspond à la taille des fréquences. Il permet de voir, en un coup d’œil, la distribution des données dans chacune des catégories.
Note : Pour faciliter la construction de diagrammes à bandes, il est recommandé de demander aux élèves d’utiliser du papier quadrillé.
En 3e année, les élèves commencent à construire des diagrammes à bandes dans lesquels ils utilisent une échelle par intervalles autres que 1. Or, cette habileté n’est pas nécessairement maîtrisée lorsqu’ils arrivent au cycle moyen.
Le personnel enseignant doit donc présenter aux élèves des activités qui leur permettent de consolider cette habileté. Par exemple, il peut leur demander de représenter les fréquences du tableau suivant par le diagramme à bandes de leur choix.
Anniversaires de naissance selon les saisons
| Saison | Nombres d'élèves |
|---|---|
| hiver | 24 |
| printemps | 30 |
| été | 48 |
| automne | 34 |
Certains élèves pourraient utiliser des intervalles de 1 et construire un diagramme à bandes verticales (ou un diagramme à bandes horizontales tracé sur la longueur de la feuille). Dans ce cas, la bande la plus longue sera formée de 48 carrés. D’autres pourraient utiliser des intervalles de 2 ou de 3 et construire leur diagramme à bandes horizontales sur la largeur de la feuille. Le personnel enseignant peut ensuite inciter les élèves à comparer les différents diagrammes construits, à discuter des avantages et des inconvénients de chacun et à déterminer lequel leur plaît le plus. Par exemple :
- Avec un intervalle de 1, on peut lire plus facilement la longueur des bandes. Par contre, le diagramme est très long et peu large; il occupe beaucoup de place, ce qui lui donne un aspect peu plaisant.
- Avec un intervalle de 2, le diagramme à bandes horizontales prend presque toute la largeur de la page. Il est lui aussi long et peu large.
- Avec un intervalle de 3, il faut faire plus attention pour déterminer la longueur de certaines bandes (par exemple, la bande qui représente 34 élèves). Par contre, le diagramme ne prend qu’environ la moitié de la largeur de la page et le rapport entre la longueur et la largeur du diagramme fait qu’il est plaisant à regarder. Les élèves pourraient alors convenir que l’échelle de 1 carré pour 3 élèves est la plus pratique.
Après un certain temps, les élèves pourraient raisonner comme suit.
- Je veux que mon diagramme occupe environ la moitié de la largeur de la page.
- Selon le tableau de fréquences, les données vont jusqu’à 48.
- Si chaque carré représente 1 élève, je n’ai pas assez de place.
- Si chaque carré représente 2 élèves, ça prend toute la largeur de la page.
- Si chaque carré représente 3 élèves, ça prend à peu près la moitié de la page.
- Donc, je peux numéroter l’axe horizontal de 0 à 48 en comptant par intervalles de 3.
Ils obtiendraient ainsi le diagramme suivant.
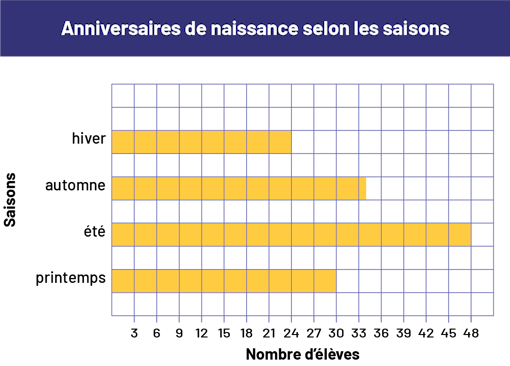Un diagramme à 4 bandes jaunes horizontales s’intitule « Anniversaires de naissance selon les
saisons ». L’axe horizontal est nommé « Nombre d’élèves », et l’axe vertical est nommé « Saisons ». Au printemps, la
bande indique 30 élèves. À l’été, la bande indique 48 élèves. À l’automne, la bande indique un peu plus de 33 élèves.
Et à l’hiver, la bande indique 24 élèves.
Les fréquences 24, 30 et 48 sont des multiples de 3 et les bandes qui les représentent arrivent précisément sur des lignes verticales. Pour représenter la fréquence 34, les élèves doivent comprendre que puisque chaque carré représente 3 élèves, il faut diviser le dernier carré utilisé en 3 parties égales. Les élèves éprouvent parfois de la difficulté à placer les nombres le long de l’axe numérique lorsqu’ils doivent représenter des intervalles autres que 1. Par exemple, certains élèves ont tendance à inscrire d’abord 1, 2, 3, puis à poursuivre en inscrivant les nombres par intervalles de 3 comme illustré ci-dessous.
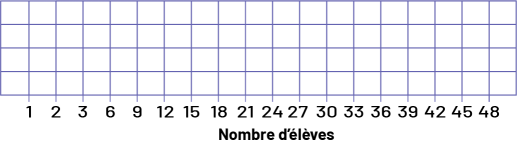
Le personnel enseignant doit donc leur faire réaliser que ceci est incorrect puisque les trois premiers carrés représentent 1 élève chacun alors que les carrés subséquents en représentent 3.
Caractéristiques d’un diagramme à bandes
- Il a un titre (par exemple, Anniversaires de naissance selon les saisons).
- Il a un axe (vertical ou horizontal) gradué selon une échelle appropriée.
- Il a un autre axe qui représente des catégories (par exemple, printemps, été, automne, hiver).
- Les deux axes ont chacun une étiquette (par exemple, Nombre d’élèves, Saisons).
- Les bandes ont la même largeur et leur longueur correspond, en fonction de l’échelle retenue, à la taille de la fréquence qu’elles représentent (par exemple, si l’échelle est par intervalles de 1, une bande de longueur 3 représente une fréquence de 3).
- Les bandes sont séparées par des espaces égaux.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 71-74.