D1. Littératie statistique :
Traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne.
SITUATION D’APPRENTISSAGE 1 : UNE COURSE OLYMPIQUE!
Durée totale : environ 4 heures
Sommaire :
Les élèves mènent une enquête afin de déterminer le temps requis par chacun et chacune pour compléter la course du 100 mètres. Les résultats sont enregistrés et représentés à l’aide d’un diagramme à pictogrammes ou à bandes. Par la suite, les élèves analysent et interprètent ces données.
| Attente | Contenus d'apprentissage |
|---|---|
| D1. Littératie statistique
traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne. |
D1.2 Collecter des données au moyen d’observations, d’expériences et d’entrevues pour répondre à des questions d’intérêt concernant les données qualitatives et quantitatives, et organiser les données à l’aide de tableaux de fréquences. D1.3 Représenter des ensembles de données, en utilisant la correspondance un à plusieurs, à l’aide de diagrammes à pictogrammes et de diagrammes à bandes comprenant des sources, des titres, des étiquettes et des échelles appropriés. D1.5 Analyser divers ensembles de données présentées de différentes façons, y compris dans des tableaux de fréquences et des diagrammes à différentes échelles, en se posant des questions au sujet des données, en y répondant et en tirant des conclusions, et ensuite formuler des arguments persuasifs et prendre des décisions éclairées. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves à mettre en pratique les quatre étapes du processus d’enquête, c’est-à-dire :
- cerner la situation;
- faire une collecte de données;
- organiser les données (notamment en les regroupant par intervalles de classe);
- analyser les données et interpréter les résultats.
| Contexte pédagogique | Préalables |
|---|---|
|
En 3e année, les élèves continuent à développer leur compréhension du processus d’enquête qui sous-tend le domaine Données. Dans la présente situation d’apprentissage, ils ont l’occasion d’effectuer une collecte de données primaires dans un contexte authentique et d’utiliser une correspondance de un à plusieurs pour représenter les résultats dans un diagramme. De plus, l’étendue des données recueillies est telle qu’ils sont incités à réduire le nombre de catégories utilisées dans leur diagramme en les regroupant par intervalles de classe. |
Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent pouvoir :
|
Matériel
- copie de l’annexe 3.1 (Liste d’activités hivernales);
- copie de l’annexe 3.2;
- ruban pour mesurer une piste de 100 mètres au gymnase ou à l’extérieur;
- chronomètres (au moins 2);
- grandes feuilles de papier (1 feuille par équipe de deux);
- marqueurs;
- cubes emboîtables.
Vocabulaire mathématique
enquête, question d’intérêt, données, catégories, intervalles de classe, tableau de dénombrement, tableau de fréquences, diagramme à pictogrammes, légende, correspondance de un à un, correspondance de un à plusieurs, diagramme à bandes, échelle, axe, titre du diagramme, chronomètre
Activité préparatoire
Durée : environ 50 minutes
Cette activité a pour but de conscientiser les élèves au fait que dans certaines situations d’enquête, il est utile de regrouper les données par intervalles de classe. Présenter l’annexe 3.1 (Liste d’activités hivernales). Expliquer aux élèves qu’on a présenté à quelques classes de 3e année une liste de 15 activités hivernales et qu’on leur a demandé d’indiquer à combien de ces activités ils aimeraient participer lors d’une journée de plein air. Leur indiquer que le tableau représente les données correspondant aux résultats du sondage.
Vérifier l’habileté des élèves à lire les données dans un tableau en posant des questions telles que :
- Comment se nomme ce genre de tableau? (Tableau de fréquences)
- Quel est le titre du tableau? (Nombre d’activités hivernales auxquelles les élèves de 3e année aimeraient participer lors d’une journée de plein air)
- Quelle question a-t-on pu poser aux élèves pour obtenir ces données? (Parmi les 15 activités hivernales suivantes, à combien aimerais-tu participer lors d’une journée de plein air?)
- Comment les réponses sont-elles regroupées? (Elles sont regroupées en catégories selon le nombre d’activités auxquelles les élèves aimeraient participer.)
- Quels renseignements sont contenus dans la 1re rangée du tableau? (Six élèves ont indiqué qu’ils aimeraient participer à 1 seule activité.)
- Quels renseignements sont contenus dans la 7e rangée du tableau? (Neuf élèves ont indiqué qu’ils aimeraient participer à 7 activités.)
- Ces données nous permettent-elles de savoir quelle est l’activité la plus populaire? (Non, ces données nous indiquent combien d’élèves ont choisi 1 activité, 2 activités, etc., sans toutefois préciser lesquelles.)
Distribuer des cubes emboîtables à deux élèves et leur demander de représenter les données du tableau de fréquences à l’aide de ce matériel concret.
Demander ensuite aux élèves d’observer les tours de cubes qu’ils ont construites et faire ressortir le fait qu’il est difficile de tirer beaucoup de conclusions à partir de cette représentation en raison du grand nombre de catégories de réponses. Leur suggérer qu’il pourrait être utile de regrouper les données dans des intervalles de classe afin de réduire le nombre de catégories. Discuter des intervalles possibles, par exemple :
- si on regroupe les données par intervalles de 3, on obtient cinq catégories;
- si on regroupe les données par intervalles de 5, on obtient trois catégories;
- si on regroupe les données par intervalles de 2, on obtient huit catégories.
Regrouper les élèves et distribuer à chaque équipe des cubes emboîtables. Leur demander de regrouper les données selon les intervalles de classe de leur choix et de les représenter ensuite à l’aide de ce matériel.
Exemples
- Une équipe a regroupé les données par intervalles de 3 (1-3, 4-6, 7-9, 10-12 et 13-15) et construit cinq tours de cubes (Photo 1).
- Une équipe a regroupé les données par intervalles de 5 (1-5, 6-10 et 11-15) et construit trois tours de cubes (Photo 2).


Demander aux élèves de comparer les différentes représentations et d’indiquer certains renseignements que l’on peut tirer de chacune. Par exemple, à partir de la représentation par intervalles de 3, ils pourraient dire que la catégorie 7 à 9 est celle qui représente le nombre d’activités auxquelles le plus grand nombre d’élèves ont indiqué vouloir participer. Ils pourraient aussi souligner qu’à partir de chacune des représentations, on peut conclure qu’un très petit nombre d’élèves souhaitent participer à plus de 10 activités.
Par la suite, les élèves pourraient construire un diagramme à pictogrammes ou un diagramme à bandes en utilisant les intervalles de classe retenus lors de la construction de la représentation concrète.
Avant l’apprentissage (mise en train)
Durée : environ 100 minutes
Faire une recherche avec les élèves sur les Jeux olympiques ou lire un album jeunesse qui contient ce thème. Leur présenter ensuite l’épreuve de la course du 100 mètres, une des épreuves faisant partie des Jeux olympiques d’été, en leur expliquant qu’un trajet de 100 mètres correspond environ à la longueur d’un terrain de football.
Montrer aux élèves les résultats obtenus au fil des années par les médaillés d’or du 100 mètres masculin en présentant l’annexe 3.2. Encourager les élèves à compléter l’annexe avec les résultats des plus récents Jeux Olympiques. Inciter les élèves à interpréter ces données en posant des questions telles que :
- Comment le tableau est-il organisé?
- Quels renseignements ce tableau nous donne-t-il?
- Que remarquez-vous au sujet des résultats? (Ils sont indiqués en secondes et en parties de seconde. Par exemple, le résultat 9,95 signifie que l’athlète a complété la course en 9 secondes et 95 parties sur 100 d’une autre seconde, soit presque 10 secondes.)
- Qui a couru le plus vite? le moins vite? (Donovan Bailey, Allen Well)
- Pourquoi l’écart entre les résultats est-il si minime?
- D’après vous, quels seraient les résultats de ces mêmes athlètes au 200 mètres? Pourquoi?
Demander à chaque élève d’estimer le nombre de secondes qu’il ou elle pense prendre pour compléter la course du 100 mètres. Leur proposer ensuite de mener une enquête afin de vérifier dans quelle mesure ils ont vu juste.
Cerner la situation
Demander aux élèves de formuler une question d’intérêt afin de préciser l’intention de l’enquête (par exemple, En combien de temps les élèves de 3e année courent-ils le 100 mètres?). Leur rappeler que la question doit être formulée clairement et qu’elle doit mener à une collecte de données.
Avec les élèves, mesurer un trajet de 100 mètres au gymnase ou dans la cour de l’école. Mettre à leur disposition quelques chronomètres.
Note : Si les élèves n’ont jamais utilisé un chronomètre, leur permettre à tour de rôle d’explorer son fonctionnement afin de s’assurer qu’ils sont capables de le démarrer, de l’arrêter et de le remettre à 0.
Faire une collecte de données
Discuter de la méthode la plus efficace pour recueillir et enregistrer les résultats de chaque élève en posant des questions telles que :
- Quelle information veut-on recueillir? (Le temps requis par chaque élève pour courir le 100 mètres.)
- Comment peut-on enregistrer les résultats? (En les inscrivant dans un tableau.)
- Est-il nécessaire d’écrire le nom des élèves lorsqu’on enregistre les résultats? Pourquoi? (Non, il n’est pas nécessaire d’écrire le nom de chaque élève parce qu’on s’intéresse seulement au temps requis pour courir le 100 mètres. Par contre, on peut le faire pour s’assurer que tous les élèves font la course et que personne ne la fait deux fois.)
- Comment peut-on s’assurer que la durée de chaque course est bien mesurée? (Chaque course peut être chronométrée par deux personnes. Si les résultats sont trop différents, on demande à l’élève de faire la course de nouveau.)
Préparer sur une grande feuille, un tableau pour enregistrer les résultats de la course. Discuter des composantes essentielles du tableau, soit :
- le titre (par exemple, Résultats des élèves au 100 m);
- le nombre de colonnes ou de rangées nécessaires;
- la désignation de chaque colonne ou rangée (par exemple, Nom et Résultat en secondes).
Demander aux élèves, à tour de rôle, d’effectuer la course du 100 mètres. Lorsque les élèves ont terminé leur course, on leur donne leur résultat et on leur demande de l’inscrire dans un tableau.
Lorsque tous les élèves ont couru le 100 mètres, transcrire les résultats à l’ordinateur et imprimer une copie du tableau des résultats pour chaque équipe de deux élèves.
Exemple
| Résultats des élèves au 100 m | |
|---|---|
| Nom | Résultat en secondes |
| Oriana | 35 |
| Isabel | 30 |
| Louise | absente |
| Terece | absente |
| Mireille | 29 |
| Julien | 26 |
| Chloé | 32 |
| Mia | 25 |
| Sienna | 30 |
| Patrick | 30 |
| André | 30 |
| Daniel | 26 |
| Matthias | 27 |
| Jean-Yves | 29 |
| Nicolas | 25 |
| Severn | 37 |
| Éloïse | 29 |
| Nicolas L. | 26 |
| Jack | 27 |
| Cameron | 37 |
| Alicia | 29 |
Pendant l’apprentissage (exploration)
Durée : environ 60 minutes
Organiser les données
Grouper les élèves et distribuer à chaque équipe une copie du tableau des résultats des courses. Leur demander de représenter ces résultats dans un tableau de fréquences.
Exemple
Résultats des élèves de la classe à la course du 100 m
| Nombre de secondes | Dénombrement | Nombre d'élèves |
|---|---|---|
| 25 |
| | |
2 |
| 26 |
| | | |
3 |
| 27 |
| | |
2 |
| 29 |
| | | | |
4 |
| 30 |
| | | | |
4 |
| 32 |
| |
1 |
| 35 |
| |
1 |
| 37 |
| | |
2 |
Distribuer une grande feuille à chaque équipe et leur demander de représenter les résultats à l’aide du diagramme de leur choix.
Circuler et observer le travail des élèves. Au besoin, intervenir en posant des questions telles que :
- Quelle est la question d’intérêt de notre enquête?
- Comment représentez-vous les résultats de la course dans chaque catégorie?
- Quels intervalles avez-vous choisis pour définir les catégories?
En circulant, choisir quelques diagrammes à pictogrammes et quelques diagrammes à bandes qui seront utilisés lors de l’échange mathématique. S’assurer que les diagrammes choisis présentent une certaine diversité par rapport à leurs composantes (titre, désignation des axes, catégories, légende, intervalles de classe).
Après l’apprentissage (objectivation/échange mathématique)
Durée : environ 40 minutes
Analyser les données et interpréter les résultats
Regrouper les élèves. Afficher d’abord les diagrammes à pictogrammes choisis lors de l’exploration. Inciter les élèves à analyser les données présentées en posant des questions reliées à chaque diagramme.
Note : Le questionnement présenté dans ce qui suit est propre à certains diagrammes obtenus lors de la mise à l’essai de la situation d’apprentissage; il vise à donner un exemple de pistes à suivre lors de l’échange mathématique. Il est préférable de ne travailler que quelques concepts par diagramme afin que ce ne soit pas toujours le travail d’une même équipe qui soit analysé. Modifier le questionnement selon les diagrammes produits par les élèves.
Exemple 1
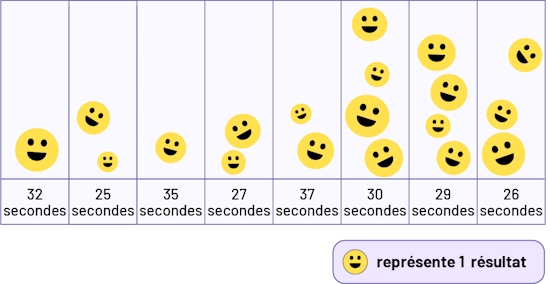
- Savons-nous ce que représente le diagramme? Pourquoi? (Non, parce qu’il n’y a pas de titre.)
- Qu’est-ce qu’un pictogramme représente? Comment le savez-vous? (Chaque pictogramme représente un élève. Ceci est indiqué dans la légende.)
- Que remarquez-vous au sujet des catégories? (Elles ne sont pas en ordre croissant et chacune ne représente qu’un seul temps de course.)
- Comment ceci peut-il nous induire en erreur? (Puisque 32 secondes est la première catégorie, on peut penser à tort qu’il s’agit du temps le plus court que les élèves ont pris pour courir le 100 mètres.)
Exemple 2
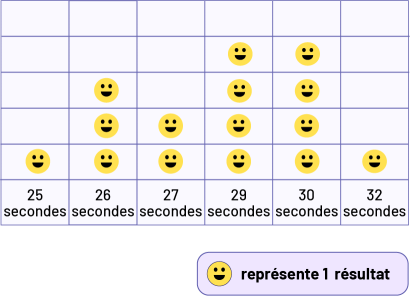
- Comment ce diagramme diffère-t-il du premier? (Les pictogrammes sont encadrés et les catégories sont placées en ordre croissant.)
- Pourquoi certains nombres entre 25 et 37 n’ont-ils pas été inscrits comme catégorie? (Parce que ces nombres correspondent à des temps de course qui n’ont pas été atteints.)
- Est-il important d’ajouter ces nombres? Pourquoi? (Oui, c’est important parce qu’une catégorie qui n’a pas de données fournit de l’information. Si cette catégorie n’apparaît pas sur le diagramme, on pourrait avoir l’impression que tous les temps de 25 à 37 secondes ont été atteints.)
- Si on inscrivait toutes les catégories de 25 à 37, il y aurait 13 catégories dans le diagramme. Que pourrait-on faire pour réduire ce nombre? (On pourrait regrouper les catégories par intervalles de classe.)
Exemple 3

- Que pensez-vous du pictogramme utilisé dans ce diagramme? (Ce n’est peut-être pas le meilleur choix de pictogramme parce qu’on peut avoir l’impression que le diagramme représente les résultats d’une enquête au sujet des poissons.)
- Comment les données ont-elles été regroupées? Quels sont les avantages et les désavantages de ce regroupement? (Elles ont été regroupées en trois catégories selon des intervalles de 5 secondes. On peut donc voir que la majorité des élèves courent le 100 mètres dans un temps qui varie entre 25 et 29 secondes. Par contre, on pourrait effectuer une interprétation plus précise des résultats si on avait un diagramme avec des intervalles de temps moins grands.)
Exemple 4
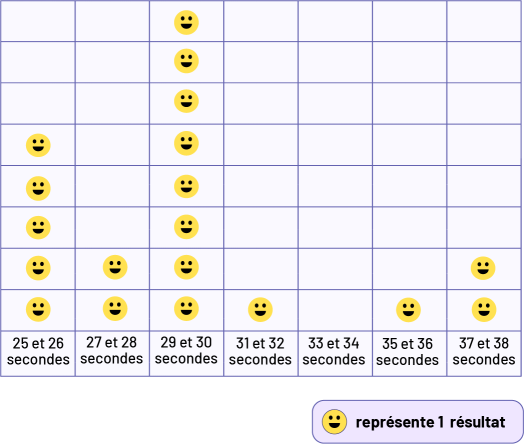
Note : Avec ce diagramme, on illustre un questionnement qui touche aux trois niveaux de compréhension.
Lire les données (niveau 1)
- En quoi ce diagramme diffère-t-il du précédent? (Les catégories correspondent à des intervalles de 2 secondes et elles sont représentées au bas du diagramme. Chaque pictogramme représente 1 élève.)
- Dans quel intervalle de temps retrouve-t-on le plus grand nombre de données? (Dans l’intervalle de 29 à 30 secondes.)
- Quel renseignement pouvons-nous tirer du diagramme par rapport à la catégorie de 33 à 34 secondes? (On constate qu’aucun élève n’a couru le 100 mètres en 33 ou en 34 secondes.)
- Combien d’élèves ont couru le 100 mètres en 25 secondes? (Il n’est pas possible de répondre à cette question à partir du diagramme. Tout ce que nous pouvons dire est que 5 élèves ont réussi la course en 25 ou 26 secondes.)
Établir des liens entre les données (niveau 2)
- Que pouvez-vous dire en comparant les données de certaines des catégories? (Il y a autant d’élèves dans l’intervalle de classe de 27 à 28 secondes que dans l’intervalle de classe de 37 à 38 secondes.)
Note : Encourager l’emploi des expressions il y a « plus que », « moins que » ou « autant que » lorsque les élèves comparent les données.
- Combien d’élèves ont couru le 100 mètres en 30 secondes ou moins? (15 élèves)
Lire au-delà des données (niveau 3)
- Quelle réponse pourrait-on donner à la question d’intérêt que nous avons formulée au début de l’enquête, soit En combien de temps les élèves de 3e année courent-ils le 100 mètres? (On pourrait dire que les élèves de 3e année prennent entre 25 et 37 secondes pour courir le 100 mètres, mais que la majorité le réussit en 30 secondes ou moins.)
- En vous basant sur les données du diagramme, quels seraient selon vous, les résultats de la classe à la course du 200 mètres? Justifiez votre réponse. (Les résultats du 200 mètres pourraient se situer dans l’intervalle de 50 à 74 secondes parce que si on double la longueur de la course, on va doubler le temps. On pourrait même anticiper que ce sera encore plus, puisqu’on risque de ralentir avant la fin de la course en raison de la fatigue.)
- Croyez-vous que les élèves d’une autre classe de 3e année obtiendraient les mêmes résultats à la course du 100 mètres? Pourquoi? (Il pourrait y avoir certaines différences, mais puisque ces élèves ont le même âge que nous, les résultats devraient être semblables.)
- Si on courait à l’extérieur plutôt qu’au gymnase, les résultats seraient-ils les mêmes? (Ils pourraient être un peu différents en raison de la différence entre les parcours.)
- Que pourriez-vous faire pour améliorer votre résultat personnel? (Je pourrais m’entraîner à courir. Je pourrais faire la course dehors puisque c’est une piste droite.)
- Pourquoi y a-t-il autant de différence entre vos résultats et ceux des coureurs olympiques? (Parce que les coureurs olympiques sont des adultes et qu’ils se sont entraînés longtemps avant de participer à cette épreuve.)
Afficher ensuite les diagrammes à bandes choisis lors de l’exploration et reprendre la même démarche en adaptant le questionnement aux composantes particulières du diagramme à bandes (par exemple, disposition des bandes, choix de l’échelle). Faire ressortir les similitudes et les différences entre ces diagrammes et les diagrammes à pictogrammes précédents.
Différenciation pédagogique
La situation d’apprentissage peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|---|---|
|
Mettre à la disposition des élèves :
|
Demander aux élèves :
|
Suivi à la maison
À la maison les élèves peuvent :
- faire une recherche sur les résultats de la course du 400 mètres aux Jeux olympiques et comparer ces résultats à ceux obtenus lors de l’enquête;
- courir le 100 mètres avec des membres de la famille, chronométrer les courses à l’aide d’une montre et enregistrer les résultats dans un tableau. Le lendemain, ils peuvent comparer l’étendue des données recueillies par l’ensemble des élèves à celle obtenue lors de l’enquête (par exemple, de 25 à 37 secondes).
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 235-247.
SITUATION D’APPRENTISSAGE 2 : DES LIVRES BIEN CLASSÉS!
Durée totale : environ 200 minutes
Sommaire
Dans cette situation d’apprentissage, les élèves appliquent le processus d’enquête au classement de livres illustrés.
| Attente | Contenus d'apprentissage |
|---|---|
| D1. Littératie statistique
traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne. |
D1.1 Trier et classer des ensembles de données portant sur des personnes ou des objets en fonction de deux ou trois attributs, en utilisant des tableaux et des logigrammes, y compris des diagrammes de Venn et de Carroll, et des diagrammes en arbre. D1.2 Collecter des données au moyen d’observations, d’expériences et d’entrevues pour répondre à des questions d’intérêt concernant les données qualitatives et quantitatives, et organiser les données à l’aide de tableaux de fréquences. D1.3 Représenter des ensembles de données, en utilisant la correspondance un à plusieurs, à l’aide de diagrammes à pictogrammes et de diagrammes à bandes comprenant des sources, des titres, des étiquettes et des échelles appropriés. D1.5 Analyser divers ensembles de données présentées de différentes façons, y compris dans des tableaux de fréquences et des diagrammes à différentes échelles, en se posant des questions au sujet des données, en y répondant et en tirant des conclusions, et ensuite formuler des arguments persuasifs et prendre des décisions éclairées. |
Intention pédagogique
Cette situation d’apprentissage a pour but d’amener les élèves à :
- recueillir des données primaires;
- construire un diagramme à bandes;
- créer et à interpréter un diagramme de Venn;
- effectuer un classement selon certains critères;
- mettre en pratique les étapes du processus d’enquête.
| Contexte | Préalables |
|---|---|
|
Au cycle primaire, les élèves ont utilisé, en situation d’enquête, différentes façons de recueillir et d’enregistrer des données (par exemple, tableau de fréquences), et de les représenter (par exemple, diagramme à pictogrammes, diagramme à bandes, diagramme de Venn). En 3e année, ils approfondissent, toujours à l’aide du processus d’enquête, leurs habiletés relatives à l’interprétation de résultats et à la construction de différents diagrammes. |
La présente situation d’apprentissage permet aux élèves de développer leurs habiletés reliées au traitement des données en utilisant le processus d’enquête pour résoudre une situation-problème. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent pouvoir construire et interpréter :
|
Matériel
- livres illustrés (1 par équipe);
- marqueurs;
- règles;
- cerceaux (3, facultatif);
- contenants (4);
- papillons autocollants;
- annexe 4.1 (1 par équipe);
- annexes 4.2, 4.4 et 4.5 (1 copie de chacune par équipe);
- annexe 4.3 (1 copie par élève);
- annexe 4.6 (facultatif).
Vocabulaire mathématique
collecte de données, diagramme à bandes horizontales, diagramme à bandes verticales, diagramme de Venn, critère d’inclusion, échelle, tableau de fréquences, étiquette
Activité préparatoire facultative
Cette activité préparatoire facultative permet aux élèves d’actualiser, au besoin, leurs connaissances relatives à la construction et à l’interprétation d’un diagramme de Venn. Tracer au tableau un diagramme de Venn (Figure 1) et identifier chaque ensemble par un des critères d’inclusion suivants : multiple de 2, multiple de 5 et nombre plus grand que 25. Rappeler aux élèves que chaque critère sert à déterminer si un élément (nombre, objet…) est inclus dans l’ensemble ou s’il en est exclu.
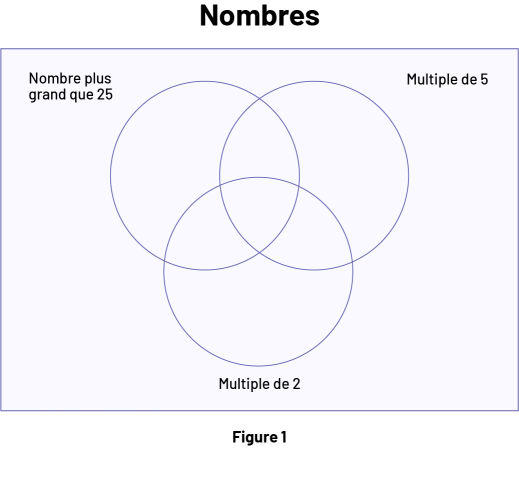
Situer quelques nombres (par exemple, 5, 12 et 20) dans le diagramme (Figure 2) et demander aux élèves de les interpréter (par exemple, l’endroit où est placé le nombre 20 dans ce diagramme permet de montrer qu’il est à la fois un multiple de 2 et un multiple de 5, mais qu’il n’est pas supérieur à 25).
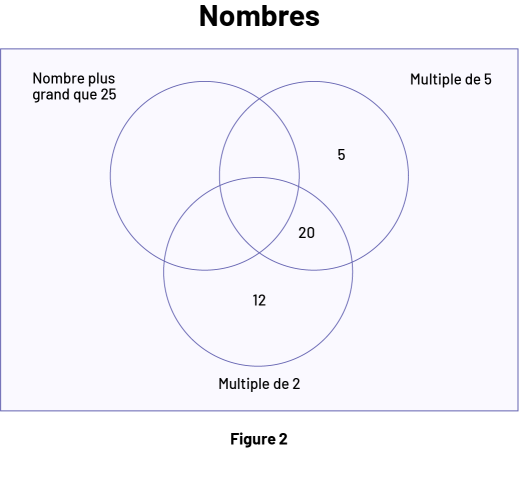
Inviter ensuite les élèves à situer d’autres nombres (par exemple, 63, 6, 7, 57, 52, 10, 18, 28, 13, 15, 35, 40, 31) dans le diagramme en fonction des critères et à expliquer leur raisonnement.
Avant l’apprentissage (mise en train)
Durée : environ 20 minutes
Jour 1
Choisir préalablement les livres illustrés à classer. Identifier chaque livre par une lettre inscrite sur deux papillons autocollants (l’utilité du deuxième papillon est expliquée plus loin). Prévoir un livre par équipe.
Note : Les élèves auront à classer ces livres en fonction de trois attributs : la taille de la police de caractères, la longueur des phrases et le nombre de phrases qu’ils contiennent. Il importe donc que les livres choisis représentent un éventail de ces attributs. Plus les livres se ressemblent, plus il sera difficile pour les élèves de définir les critères d’inclusion. Des livres qui contiennent une courte histoire se prêtent mieux à cette activité que des livres documentaires, des recueils de textes ou des bandes dessinées.
Présenter la situation d’apprentissage suivante aux élèves :
Dans la classe de 2e année de Mme Isabelle* , les livres du centre de lecture ne sont pas classés. Elle nous demande de l’aider à les classer en quatre groupes selon leur niveau de difficulté de lecture. Les livres d’un même groupe seront mis dans un même contenant. Elle précise que le niveau de difficulté d’un livre doit être déterminé en fonction des attributs suivants : la taille de la police de caractères, le nombre total de phrases par livre et le nombre de mots dans 10 phrases.
* Pour rendre la situation plus authentique, utiliser le nom d’un membre du personnel de l’école.
Pour aider les élèves à cerner la situation, présenter pour chacun des attributs deux livres préalablement choisis en leur demandant lequel est le plus facile à lire. Laisser les élèves expliquer leur choix. Ainsi, présenter :
- un livre dont la taille de la police de caractères est grande (par exemple, 14 points, 16 points) et un autre dont la taille est plus petite (par exemple, 10 points, 8 points);
- un livre ayant peu de phrases (peu de texte) et un autre ayant beaucoup de phrases (beaucoup de texte);
- un livre ayant de courtes phrases et un autre ayant de longues phrases (lire un passage de chacun des livres).
Expliquer brièvement le sens de ces trois attributs.
- La taille de la police de caractères : La police de caractères est la forme d’écriture des lettres dans une publication (par exemple, Arial Narrow ou Times New Roman). La taille de la police de caractères est définie en points. Projeter l’annexe 4.1 (Taille de la police de caractères) afin de montrer aux élèves, par exemple, qu’un caractère dont la taille est de 10 points est plus petit qu’un caractère dont la taille est de 16 points.
- Le nombre total de phrases par livre : Revoir ce qu’est une phrase. En général, la façon de reconnaître une phrase est d’en trouver les limites, soit avec la lettre majuscule qui en marque le début et le point qui en marque la fin.
- Le nombre de mots dans 10 phrases : Un attribut souvent utilisé pour évaluer le niveau de difficulté de lecture d’un livre est le nombre moyen de mots par phrase, c’est-à-dire la longueur moyenne des phrases. Cependant, puisque les élèves de 3e année n’ont pas encore maîtrisé parfaitement le concept de la moyenne, il suffit de leur expliquer qu’ils devront compter le nombre total de mots dans 10 phrases choisies au hasard dans le texte.
Pendant l’apprentissage (exploration)
Durée : environ 50 minutes
Note : Le classement des livres s’effectuera selon des critères reliés aux attributs. Pour déterminer ces critères, il faut préalablement avoir de l’information au sujet des livres qui feront l’objet du classement. C’est pourquoi les élèves devront d’abord effectuer une collecte de données sur les trois attributs : la taille de la police de caractères, le nombre total de phrases dans le livre et le nombre de mots dans 10 phrases choisies au hasard.
Grouper les élèves et remettre à chaque équipe un livre identifié par une lettre, l’annexe 4.1 (Taille de la police de caractères) ainsi qu’une copie de l’annexe 4.2 (Données reliées aux livres à classer).
Modeler une façon de déterminer la taille de la police de caractères utilisée dans un livre. Inviter ensuite les équipes à déterminer quelle taille est utilisée dans leur livre et à l’inscrire à l’annexe 4.2. Circuler parmi les équipes et aider les élèves au besoin.
Une fois que toutes les équipes ont terminé, revoir brièvement la définition d’une phrase et modeler une stratégie pour déterminer le nombre total de phrases dans un livre. Inviter les équipes à faire de même avec leur livre et à inscrire le résultat à l’annexe 4.2. Circuler parmi les équipes et aider les élèves au besoin. Modeler ensuite une stratégie pour déterminer le nombre de mots dans 10 phrases choisies au hasard, puis demander aux équipes de procéder de la même façon avec leur livre et d’inscrire le résultat à l’annexe 4.2.
En groupe classe, insister sur le fait que chaque équipe a recueilli les données relatives à son livre. En discutant avec les élèves, les amener à reconnaître que pour déterminer les critères de classement des livres selon leur niveau de difficulté de lecture, il est important d’avoir une vue d’ensemble des données recueillies. Leur suggérer que les tableaux de l’annexe 4.2 s’avéreraient utiles pour organiser les données.
Reproduire sur de grandes feuilles de papier les trois tableaux. Demander, tour à tour, à chaque équipe de venir inscrire leurs résultats dans ces tableaux et aux autres élèves de remplir leurs tableaux de l’annexe 4.2 au fur et à mesure que les données sont fournies.
Une fois les tableaux remplis, amorcer une interprétation des résultats en incitant les élèves à énoncer des conclusions (par exemple, dans l’ensemble des livres, la police 14 est la plus utilisée; certains livres présentent peu de phrases; plusieurs livres ont des phrases courtes).
Animer l’échange en posant des questions telles que :
- Est-ce qu’à première vue ces données permettent de classer les livres en quatre catégories? (Non)
- Est-ce que certaines données peuvent nous aider à faire des groupes de livres? (Oui, si on compare un attribut à la fois. Par exemple, un livre qui comporte de nombreuses phrases est plus difficile à lire qu’un livre qui en a moins.)
- Mme Isabelle a choisi ses attributs afin que le classement reflète le niveau de difficulté de lecture des livres. D’après nos résultats, est-ce que le livre A est plus facile ou plus difficile à lire que le livre G? (Le livre G contient moins de phrases et moins de mots que le livre A. La taille de la police du livre G est plus grande que celle du livre A. Alors, le livre G est plus facile à lire que le livre A.)
- Selon nos données, est-ce qu’un livre semble plus facile à lire qu’un autre? (Il est difficile de comparer simultanément les données dans les trois tableaux.)
- Comment peut-on percevoir plus rapidement les différences entre les livres pour un même attribut? (Il faudrait trouver une autre façon d’organiser et de représenter les données. La création d’un diagramme à bandes permettrait de jeter un regard différent sur les données.)
Jour 2
Durée : environ 60 minutes
Revoir la tâche précédente et proposer aux élèves d’organiser l’ensemble des données par attribut à l’aide de trois diagrammes à bandes.
Reformer les mêmes équipes que le jour 1 et assigner à chaque équipe la responsabilité de construire un diagramme à bandes représentant les données d’un attribut. On comptera donc plus d’une équipe travaillant au diagramme représentant un même attribut.
Distribuer à chaque élève une copie de l’annexe 4.3 (Papier quadrillé) qui servira à la construction du diagramme à bandes. Préciser que cette opération se fera en deux parties : un ou une élève construira un diagramme représentant les données d’une moitié des livres (par exemple, les livres identifiés par les lettres de A à H) et l’autre fera de même pour le reste des livres (par exemple, les livres identifiés par les lettres de I à O). Spécifier qu’ils devront ensuite réunir les deux diagrammes en un seul pour illustrer l’ensemble des données. Leur expliquer qu’il est donc important que les deux membres de l’équipe déterminent à l’avance l’orientation des bandes (bandes horizontales ou bandes verticales) et l’échelle à utiliser (par exemple, chaque carré représente 10 phrases).
Pendant que chaque élève construit sa section de diagramme, circuler parmi les équipes et les aider au besoin. Profiter de l’occasion pour repérer des diagrammes particuliers qui pourraient enrichir la discussion au cours de l’échange mathématique.
Une fois les diagrammes individuels réalisés, prendre les deux diagrammes d’une équipe et modeler la façon de les réunir, soit :
- plier le diagramme correspondant à la deuxième moitié des livres le long de l’axe vertical pour les diagrammes à bandes verticales (Figure 1) ou le long de l’axe horizontal pour les diagrammes à bandes horizontales;
- joindre les deux diagrammes à l’aide d’un ruban adhésif ou de colle (Figure 2), en prenant soin de conserver le même espace entre les bandes.
Exemple
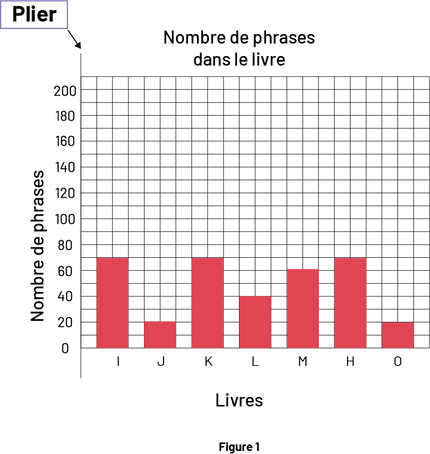
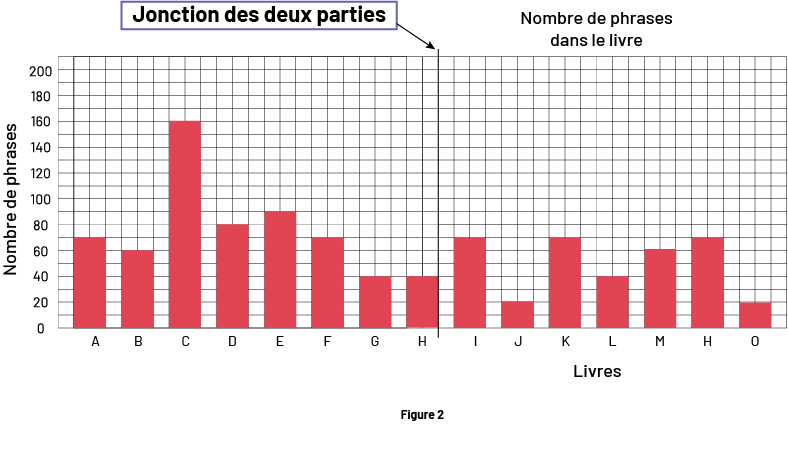
Dire aux élèves d’effacer un titre et une étiquette s’ils se retrouvent en double. Une fois tous les diagrammes réunis, les afficher au mur en les regroupant selon l’attribut. Inviter les élèves à s’approcher et à observer les diagrammes illustrant la taille de la police de caractères des livres. Convier une équipe à présenter son diagramme et à l’expliquer.
Note : À titre d’exemple, l’annexe 4.4 (Diagrammes à bandes) présente pour chaque attribut, un diagramme à bandes correspondant aux données recueillies lors de la mise à l’essai de cette situation d’apprentissage. La plupart des interprétations proposées dans ce qui suit découlent de ces diagrammes.
Inciter les élèves à interpréter les diagrammes en posant des questions telles que :
- Lequel des diagrammes est le plus facile à lire ou à interpréter? Pourquoi?
- Quel est le rôle du titre, des étiquettes, de la droite graduée et des bandes dans un diagramme à bandes?
- Quelle différence y a-t-il entre ces diagrammes? (L’échelle, l’espacement entre les bandes, le sens des bandes, la couleur des bandes, la largeur des bandes, entre autres, sont différents d’un diagramme à l’autre.)
- Quel est l’effet de l’utilisation d’une échelle différente sur un diagramme? (Plus l’échelle est grande, plus on voit clairement la différence entre les valeurs.)
- En examinant les diagrammes, quelles conclusions peut-on tirer? (Par exemple, les livres G et J ont la plus grande taille de police de caractères.)
- Quelle taille de police de caractères revient le plus souvent? Qu’est-ce que cela signifie? (C’est le 14, ce qui signifie que 14 points est la taille la plus utilisée dans nos livres.)
- Entre quelles valeurs, la taille des polices de caractères de nos livres se situe-t-elle? (Entre 12 et 22 points.)
- Est-ce plus facile de comparer la taille de la police de caractères des livres dans les diagrammes ou dans le tableau? Pourquoi? (Dans les diagrammes, car on peut comparer d’un coup d’œil la longueur des bandes et, par conséquent, la taille de la police de caractères des livres.)
Note : Le but de cet échange est de faire remarquer à la classe que tous ces diagrammes d’un même attribut représentent les mêmes données, et ce, peu importe l’échelle ou la longueur, la largeur et l’orientation des bandes.
Refaire rapidement le même exercice avec les diagrammes correspondant aux deux autres attributs. Inciter les élèves à reconnaître que, puisque chaque diagramme à bandes permet de comparer les livres en fonction d’un seul attribut, il serait utile de trouver un autre type de diagramme pour comparer les livres en fonction de plusieurs attributs. Pour ce faire, poser des questions telles que :
- À partir de tous ces diagrammes, est-il possible de classer nos livres en quatre groupes reflétant le niveau de difficulté de lecture des livres selon les trois attributs simultanément, comme le demandait Mme Isabelle? (Ça demeure difficile.)
- Est-ce qu’on pourrait utiliser une autre sorte de diagramme pour comparer en même temps les trois attributs? (Amener les élèves à suggérer le diagramme de Venn.)
Préciser que la situation d’apprentissage se poursuivra le lendemain.
Jour 3
Durée : environ 55 minutes
Revoir les tâches accomplies préalablement et expliquer aux élèves qu’ils utiliseront un diagramme de Venn qui les aidera à classer les livres selon leur niveau de difficulté de lecture.
Tracer un grand rectangle au tableau. À l’intérieur du rectangle, fixer trois cerceaux avec du ruban-cache ou dessiner trois cercles pour former un diagramme de Venn.
Indiquer aux élèves que chaque cercle regroupera les livres dont le niveau de difficulté de lecture est jugé plus élevé en fonction de l’un des attributs. Leur préciser que pour remplir le diagramme de Venn, il faut préalablement adopter, pour chaque attribut, un critère d’inclusion, c’est-à-dire le seuil à partir duquel le niveau de difficulté de lecture sera jugé plus élevé. Chaque critère doit donc permettre de différencier les livres faciles à lire des livres difficiles à lire. Il doit aussi faire en sorte qu’un certain nombre de livres y répondent et soient inclus dans cet ensemble, et que d’autres ne le soient pas.
Choisir, pour chacun des trois attributs, un diagramme parmi ceux construits par les élèves et les afficher au tableau. Inviter les élèves à examiner le diagramme à bandes représentant la taille de la police de caractères, à proposer un critère d’inclusion et à justifier leur choix. Discuter en groupe classe des propositions et convenir, par consensus, du critère d’inclusion à retenir. Inscrire ce critère comme une étiquette dans le diagramme de Venn au tableau.
Par exemple, dans le diagramme 1 de l’annexe 4.4, on constate que la taille de la police de caractères de tous les livres se situe entre 12 et 22 points. Près de la moitié des livres affichent une taille de 14 points ou moins. À partir de cette observation, on pourrait retenir comme critère d’inclusion dans le premier ensemble, les livres dont la taille de la police de caractères est de 14 points ou moins, puisqu’un texte dont les caractères sont plus petits est plus difficile à lire. Un autre critère serait tout aussi valable (par exemple, la taille est de 16 points ou moins, ou même de 18 points ou moins) pourvu qu’il soit établi par consensus.
Reprendre la même démarche pour chacun des deux autres diagrammes.
À titre d’exemples,
- dans le diagramme 2 de l’annexe 4.4, on constate que le nombre de phrases dans les livres varie entre 27 et 161. On pourrait alors convenir que le critère d’inclusion sera de 55 phrases ou plus, puisque plus il y a de phrases dans un livre, plus il risque d’être difficile à lire.
- dans le diagramme 3 de l’annexe 4.4, on constate que le total de mots dans 10 phrases s’échelonne de 55 à 162. On pourrait alors convenir que le critère d’inclusion sera de 80 mots ou plus, puisque plus il y a de mots dans un texte, plus il est difficile à lire.
Reformer les mêmes équipes que lors du jour 2 et distribuer à chacune une copie de l’annexe 4.5 (Diagramme de Venn). Leur demander de compléter les étiquettes de chaque ensemble selon ce qui a été convenu, puis de situer leur livre (à l’aide de la lettre d’identification) dans le diagramme de Venn.
Note : Il est important que les élèves justifient l’endroit où est placé leur livre. Pour leur faciliter la tâche, on peut leur suggérer de remplir une copie de l’annexe 4.6 (Analyse des critères).
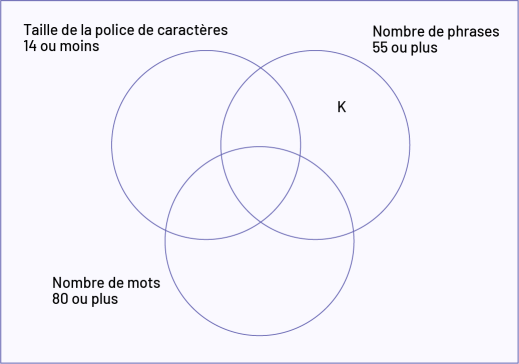
Exemple d’explication à l’aide de l’annexe 4.6
| Notre livre est identifié par la lettre K. | |
| La taille de la police de caractères est 16. | Le critère d'inclusion pour la taille de la police de caractères est 14 ou moins. Notre livre se situe donc à l'extérieur de cercle correspondant à cet attribut. |
| Dans notre livre, il y a 73 phrases. | Le critère d'inclusion pour le nombre de phrases est de 55 ou plus. Notre livre se situe donc à l'intérieur du cercle correspondant à cet attribut. |
| Dans les 10 phrases choisies, il y a 55 mots. | Le critère d'inclusion pour le nombre de mots dans 10 phrases est de 80 ou plus. Notre livre se situe donc à l'extérieur du cercle correspondant à cet attribut. |
| Notre livre se situe donc à l'extérieur du cercle pour la taille de la police de caractères, à l'intérieur du cercle pour le nombre de phrases et à l'extérieur du cercle pour le nombre de mots dans 10 phrases | |
Cette équipe indique alors l’endroit où se situe son livre comme suit.
Inviter chaque équipe à venir placer, au bon endroit sur le diagramme de Venn au tableau, l’un des papillons autocollants apposés sur la couverture de leur livre. Demander à quelques élèves de décrire ce que représente l’endroit où est situé leur livre ou celui d’une autre équipe.
Demander aux élèves de remplir au fur et à mesure leur diagramme de Venn (Annexe 4.5). Les inviter ensuite à interpréter les résultats et à énoncer des conclusions en posant des questions telles que :
- Que peut-on dire au sujet d’un livre qui est inclus dans un seul cercle? (Il répond à un seul critère.)
- Que peut-on dire au sujet d’un livre qui est inclus dans deux cercles? (Il répond à deux critères.)
- Qu’est-ce qui différencie le livre A du livre C? (Le livre A répond à deux critères, puisqu’il contient plus de 80 mots dans 10 phrases et plus de 55 phrases, mais que la taille de la police de caractères n’est pas de 14 points ou moins. Le livre C, par contre, répond aux trois critères.)
- Est-ce qu’il y a des livres qui ne remplissent aucun critère? Où les retrouve-t-on? (Oui. Ces livres sont placés dans le rectangle, mais à l’extérieur des cercles.)
- Est-ce que tous les livres répondent au même nombre de critères? (Non)
Après l’apprentissage (objectivation/échange mathématique)
Durée : environ 15 minutes
Inciter les élèves à interpréter le diagramme de Venn, en posant des questions telles que :
- Où sont situés les livres les plus faciles à lire dans le diagramme? Pourquoi dit-on qu’ils sont plus faciles à lire que les autres? (Ils sont situés à l’extérieur des trois ensembles, mais dans le rectangle. Ils sont plus faciles à lire, car selon nos données, une police de caractères relativement grande est utilisée et ces livres comptent peu de phrases et comportent des phrases courtes.)
- En fonction des attributs utilisés et des critères énoncés, où sont situés les livres les plus difficiles à lire? Comment pouvez-vous justifier leur degré de difficulté? (Ils sont situés à l’intérieur de l’intersection des trois cercles. Ils sont plus difficiles à lire, car selon nos données, une police de caractères relativement petite est utilisée et ces livres comptent un grand nombre de phrases et comportent des phrases longues.)
- Comment pourrait-on utiliser ce diagramme pour classer les livres en quatre groupes selon leur niveau de difficulté de lecture? (On peut regrouper les livres selon qu’ils ne remplissent aucun critère ou qu’ils remplissent un critère, deux critères ou trois critères.)
Placer quatre contenants devant la classe et demander à chaque équipe de déposer leur livre dans le contenant approprié, c’est-à-dire un contenant pour les livres qui ne remplissent aucun critère, un second pour ceux qui remplissent un seul critère, un troisième pour ceux qui en remplissent deux et un quatrième pour ceux qui en remplissent trois.
Poser les questions suivantes :
- Comment les livres sont-ils classés? (Ils sont classés selon leur niveau de difficulté de lecture en fonction des attributs donnés par Mme Isabelle.)
- Comment s’y prendrait-on pour classer de nouveaux livres pour la classe de Mme Isabelle? (Maintenant que l’on a établi les critères d’inclusion pour chaque attribut, on vérifierait la taille de la police de caractères, le nombre de phrases dans le livre et le nombre de mots dans 10 phrases choisies au hasard. Puis, selon le nombre de critères remplis par le livre, on le déposerait dans le contenant approprié, le classant ainsi selon son niveau de difficulté de lecture.)
Différenciation pédagogique
L’activité peut être modifiée pour répondre aux différents besoins des élèves.
| Pour faciliter la tâche | Pour enrichir la tâche |
|---|---|
|
|
Suivi à la maison
Demander aux élèves de déterminer si le choix des livres dans le centre de lecture de la classe de Mme Isabelle constitue une bonne répartition des quatre niveaux de difficulté de lecture et de construire un diagramme approprié pour justifier leur réponse. Par exemple, ils peuvent construire un diagramme à bandes pour représenter le nombre de livres correspondant à chacun des niveaux de difficulté, puis comparer la longueur des bandes. Si les longueurs sont semblables, c’est qu’il y a à peu près le même nombre de livres à chaque niveau de difficulté; la répartition est donc bonne.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 177-192.
