D2.1 Utiliser le vocabulaire mathématique, y compris des termes comme « impossible », « peu probable », « équiprobable », « très probable » et « certain » pour exprimer la probabilité que des événements se produisent, la représenter sur une ligne de probabilité et s’appuyer sur cette probabilité pour faire des prédictions et prendre des décisions éclairées.
Activité 1 : Évaluer la probabilité
Voici cinq sacs qui contiennent chacun quatre billes.
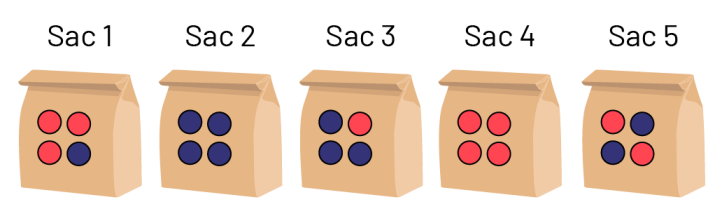 Image Cinq
sacs en papier s’alignent côte à côte. Chacun d’eux contient quatre billes. Le sac un contient trois billes rouges et
une bille violette. Le sac deux contient quatre billes violettes. Le sac trois contient une bille rouge et trois
billes violettes. Le sac 4 contient 4 billes rouges. Et le sac cinq contient deux billes rouges et deux billes
violettes.
Image Cinq
sacs en papier s’alignent côte à côte. Chacun d’eux contient quatre billes. Le sac un contient trois billes rouges et
une bille violette. Le sac deux contient quatre billes violettes. Le sac trois contient une bille rouge et trois
billes violettes. Le sac 4 contient 4 billes rouges. Et le sac cinq contient deux billes rouges et deux billes
violettes.
Demander aux élèves d’expliquer la probabilité de piger une bille rouge, en utilisant les termes mathématiques « impossible », « peu probable », « équiprobable », « très probable » et « certain».
- Sac 1 : Très probable puisqu’il y a plus de billes rouges que de billes bleues.
- Sac 2 : Impossible puisqu’il n’y a pas de billes rouges.
- Sac 3 : Peu probable puisqu’il y a seulement une bille rouge parmi les quatre.
- Sac 4 : Certain puisque toutes les billes sont rouges.
- Sac 5 : Équiprobable puisqu’il y a le même nombre de billes rouges et de billes bleues.
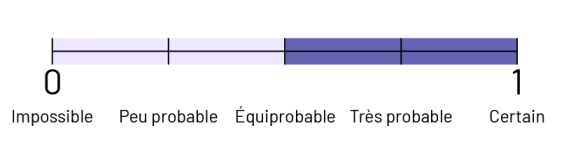
Demander aux élèves de situer chacun des événements (sacs) sur l’échelle des probabilités suivante.
Source : En avant, les maths!, 4e année, CM, Données, p. 4.
 Image
L’échelle des probabilités est graduée de zéro à un et sectionnée en quatre parties. À l’extrême-gauche, à zéro, il
est écrit « impossible ». Au premier quart, il est écrit « peu probable ». À la moitié, il est écrit « équiprobable ».
Au troisième quart, il est écrit « très probable ». Et à l’extrême-droite, à un, il est écrit « certain ». La première
moitié de la ligne est violet pâle tandis que la deuxième moitié est violet foncé.
Image
L’échelle des probabilités est graduée de zéro à un et sectionnée en quatre parties. À l’extrême-gauche, à zéro, il
est écrit « impossible ». Au premier quart, il est écrit « peu probable ». À la moitié, il est écrit « équiprobable ».
Au troisième quart, il est écrit « très probable ». Et à l’extrême-droite, à un, il est écrit « certain ». La première
moitié de la ligne est violet pâle tandis que la deuxième moitié est violet foncé.
Si l’on ajoute une bille rouge dans chacun des sacs, la probabilité de piger une bille rouge changerait-elle?
Si l’on ajoute une bille bleue dans chacun des sacs, la probabilité de piger une bille bleue changerait-elle?
ACTIVITÉ 2 : Faire des prédictions en utilisant des probabilités
Amar lance six fois un dé à six faces.

Prédire le nombre de fois qu’il obtiendra :
- un « 3 » ou un « 4 » (puisqu’il est peu probable d’obtenir un « 3 » ou un « 4 », je prédis qu’il obtiendra deux fois un de ces chiffres);
- un « 1 », « 2 », « 3 », « 4 », « 5 » ou « 6 » (puisqu’il est certain d’obtenir un chiffre de 1 à 6, je prédis alors qu’il réussira six fois à rouler un de ces chiffres);
- un « 1 », « 2 », « 4 », « 5 » ou « 6 » (puisqu’il est très probable de rouler un de ces chiffres, je prédis qu’il obtiendra à cinq reprises un « 1 », « 2 », « 4 », « 5 » ou « 6 »);
- un « 0 » (puisqu’il est impossible d’obtenir un « 0 », je prédis alors qu’il n’obtiendra jamais ce chiffre);
- un « 1 », « 2 », « 3 » ou un « 4 », « 5 », « 6 » (puisqu’il est équiprobable d’obtenir un chiffre de 1 à 3 ou un chiffre de 4 à 6, je prédis qu’il obtiendra trois fois un chiffre de 1 à 3 et trois fois un chiffre de 4 à 6).
ACTIVITÉ 3 : CHASSE AU TRÉSOR (VRAISEMBLANCE D’UN ÉVÉNEMENT)
Matériel
- ensembles de six billes de couleur différente (deux par équipe de quatre)
- sacs opaques (deux par équipe de quatre)
- annexe 1.2 (une copie par équipe de quatre)
- jetons de couleur différente (deux par équipe de quatre)
- référentiel pour la valeur des billes
Sommaire
Dans cette activité, les élèves tentent de se rendre sur l’île au Trésor en utilisant leur compréhension intuitive de la probabilité pour évaluer la vraisemblance d’un résultat particulier.
Déroulement
Former des équipes de quatre. Inviter chaque équipe à former deux groupes. Ils joueront l’un contre l’autre. Remettre à chaque équipe un plateau de jeu (voir l’annexe 1.2), deux jetons de couleur différente et deux sacs opaques contenant chacun une série de six billes de couleur différente. Expliquer aux élèves qu’une valeur est associée à chacune des billes selon sa couleur. Fixer un référentiel de ces valeurs sur chacun des sacs ou inscrire le référentiel au tableau.
| Exemple de référentiel | ||
|---|---|---|
| Bille rouge : 1 | Bille bleue : 2 | Bille verte : 3 |
| Bille jaune : 4 | Bille orange : 5 | Bille mauve : 6 |
Indiquer aux élèves que le but du jeu est d’être le premier groupe à se rendre sur l’île au Trésor. Leur expliquer les règles du jeu en modelant, au besoin, un premier tirage. Leur accorder ensuite le temps nécessaire pour jouer.
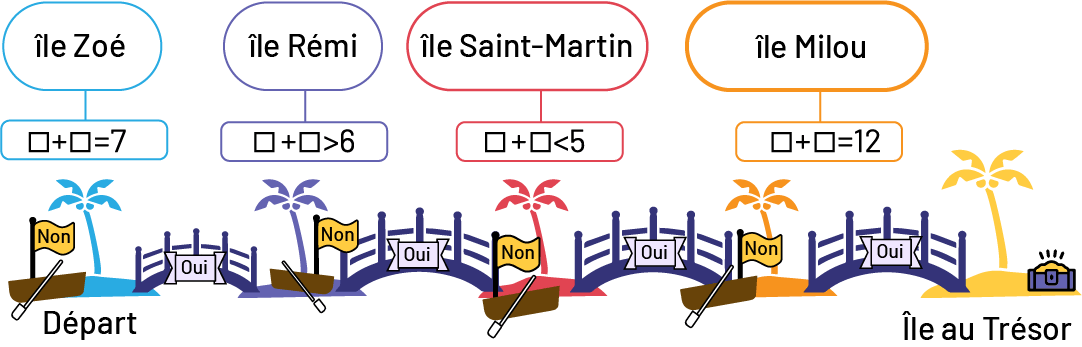 Image Cinq mini îles de différentes couleurs sont alignées côte à côte. Elles sont toutes reliées par
des ponts sur lesquels il est écrit « oui ». Elles hébergent chacune une barque dont le drapeau hissé sur le mât
indique « non ». L'île de départ, l’île zoé, est bleue et présente l’équation suivante : carré vide plus égale 7. la
deuxième, rémi, violette grand que 6. troisième, saint-martin, rouge petit cinq. quatrième, milou, orange 12. elle
mène à dernière île, au trésor, qui jaune.
Image Cinq mini îles de différentes couleurs sont alignées côte à côte. Elles sont toutes reliées par
des ponts sur lesquels il est écrit « oui ». Elles hébergent chacune une barque dont le drapeau hissé sur le mât
indique « non ». L'île de départ, l’île zoé, est bleue et présente l’équation suivante : carré vide plus égale 7. la
deuxième, rémi, violette grand que 6. troisième, saint-martin, rouge petit cinq. quatrième, milou, orange 12. elle
mène à dernière île, au trésor, qui jaune.
Règles du jeu
- Au départ, chaque groupe place son jeton sur l’île Zoé.
- Une ou un membre de chaque groupe pige à tour de rôle une bille d’un sac et le groupe qui pige la valeur la plus élevée commence le jeu.
- À tour de rôle, chaque groupe observe la phrase mathématique proposée (par exemple, ? + ? = 7). Il évalue la mesure dans laquelle il est possible de piger une bille de chaque sac afin que leur valeur rende la phrase mathématique vraie.
- Le groupe décide ensuite si oui ou non il réussira à piger les billes dont la valeur rend la phrase mathématique vraie et place son jeton soit sur le pont (pour le oui) soit sur la chaloupe (pour le non).
- Le groupe pige une bille de chaque sac. Si le résultat obtenu correspond au choix qu’il a fait (oui ou non), il déplace son jeton sur l’île suivante; sinon, il reste sur l’île Zoé jusqu’au prochain tour.
- Le premier groupe à atteindre l’île au Trésor gagne la partie.
Exemple
La phrase mathématique à compléter est ? + ? = 7. En l’observant, le groupe décide qu’il ne réussira pas à piger deux billes dont la valeur totale est égale à 7. Les élèves placent donc leur jeton sur la chaloupe. Chaque élève pige ensuite une bille d’un sac différent. Elles et ils constatent qu’une des billes pigées est bleue (2) et que l’autre est orange (5). Puisque leur valeur totale est égale à 7 et que ce résultat ne correspond pas à ce qu’elles et ils avaient prédit, les élèves replacent leur jeton sur l’île Zoé et attendent au prochain tour. Si elles et ils avaient pigé une bille rouge (1) et une bille verte (3), les élèves n’auraient pas obtenu un total de 7, ce qui aurait correspondu à leur prédiction. Elles et ils auraient alors pu placer leur jeton sur l’île suivante.
Une fois que toutes les équipes ont terminé le jeu, animer une discussion au sujet des stratégies utilisées. Par exemple, les élèves pourraient indiquer qu’il y avait peu de possibilités de rendre la dernière phrase mathématique vraie ( ? + ? = 12) et qu’il était alors préférable de choisir de placer le jeton sur la chaloupe.
Source : Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, p. 193-194.
