D2.1 use mathematical language, including the terms “impossible”, “unlikely”, “equally likely”, “likely”, and “certain”, to describe the likelihood of events happening, and use that likelihood to make predictions and informed decisions.
Activity 1: Assessing Probability
Present the students with five bags each containing four marbles that are either red or blue or a combination of red and blue.
image Five paper bags are lined up side by side. Each bag contains four marbles. Bag one contains three red marbles and one purple marble. Bag two contains four purple marbles. Bag three contains one red marble and three purple marbles. Bag four contains four red marbles. And bag five contains two red marbles and two purple marbles.
Ask students to explain the probability of drawing a red marble, using the mathematical terms "impossible," "unlikely," "equally likely," "very likely" and "certain".
- Bag 1: Very likely since there are more red marbles than blue marbles.
- Bag 2: Impossible since there are no red marbles.
- Bag 3: Unlikely since there is only one red marble among the four.
- Bag 4: Certain since all the marbles are red.
- Bag 5: Equally likely since there are the same number of red and blue marbles.
Ask students to place each event (bag) on the following probability line.
Source: translated from En avant, les maths!, 4e année, CM, Données, p. 4.
image The probability scale is graduated from zero to one and divided into four parts. On the far left, at zero, it is written "impossible". At the first quarter, it is written "somewhat likely". At half, it is written "equiprobable". At the third quarter, it is written "very likely". And on the far right, at one, it says "certain". The first half of the line is light purple while the second half is dark purple.
If we add a red marble to each of the bags, would the probability of drawing a red marble change?
If we add a blue marble to each bag, would the probability of drawing a blue marble change?
Activity 2: Making Predictions Using Probabilities
Amar rolls a six-sided die six times. Each die has the numbers 1 to 6 represented by dots as shown in the diagram below.

Predict how many rolls will have:
- a "3" or a "4" (since it is unlikely to get a "3" or a "4", I predict that he will roll one of these numbers twice);
- a "1", "2", "3", "4", "5" or "6" (since he is certain to get a number from 1 to 6, I predict that he will succeed six times in rolling one of these numbers);
- a "1", "2", "4", "5" or "6" (since it is very likely to roll one of these numbers, I predict that it will get a "1", "2", "4", "5" or "6" five times);
- a "0" (since it is impossible to get a "0", then I predict that it will never get that number);
- a "1", "2", "3" or a "4", "5", "6" (since it is equally likely to get a number from 1 to 3 or a number from 4 to 6, I predict that he will roll a number from 1 to 3 and a number from 4 to 6 three times).
Activity 3: Scavenger Hunt (Likelihood of an Event)
Materials
- sets of six different coloured marbles (two per team of four)
- opaque bags (two per team of four)
- Appendix 1.2 (one copy per team of four)
- different coloured tokens (two per team of four)
- benchmark for the value of the marble
Summary
In this activity, students attempt to get to Treasure Island by using their intuitive understanding of probability to assess the likelihood of a particular outcome.
Course of Action
Form groups of four. Invite each team to form two teams. They will play against each other. Give each group a game board (see Appendix 1.2), two different coloured tokens, and two opaque bags, each containing a set of six different coloured marbles. Explain to students that each marble has a value associated with it, depending on its colour. Attach a reference of these values to each bag or write the reference on the board.
| Example of a Reference System | ||
|---|---|---|
| Red marble: 1 | Blue marble: 2 | Green marble: 3 |
| Yellow marble: 4 | Orange marble: 5 | Purple marble: 6 |
Tell students that the object of the game is to be the first group to get to Treasure Island. Explain the rules of the game by modelling an initial draw, if necessary. Then allow them time to play.
image Five mini islands of different colors are lined up side by side. They are all connected by bridges on which it is written "yes". Each island has a boat with a flag on the mast that says "no". The starting island, Zoe Island, is blue and has the following equation: empty box plus empty box equals 7. The second, Rémi Island, is purple and has the following equation: empty box plus empty box is greater than 6. The third, Saint-Martin Island, is red and has the following equation: empty box plus empty box is smaller than five. The fourth, Milou Island, is orange and has the following equation: empty box plus empty box equals 12. It leads to the last island, Treasure Island, which is yellow.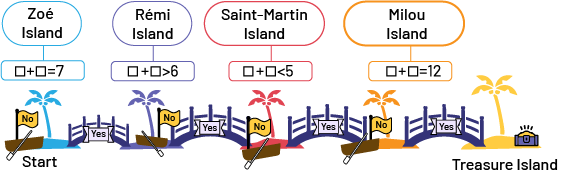
Rules of the Game
- At the start, each group places its marble on Zoe Island.
- One member of each group takes turns drawing a marble from a bag and the group that draws the highest value begins the game.
- In turn, each group looks at the proposed mathematical sentence (for example, ? + ? = 7) and assesses the extent to which it is possible to draw a marble from each bag so that their value makes the mathematical sentence true.
- The group then decides whether or not they will be able to pick the marbles whose value makes the mathematical sentence true and places their token either on the bridge (for yes) or on the rowboat (for no).
- The group picks a marble from each bag and if the result matches the choice they made (yes or no), they move their token to the next island; if not, they stay on Zoe Island until the next turn.
- The first group to reach Treasure Island wins the game.
Example
The mathematical sentence to be completed is ? + ? = 7. After observing it, the group decides that it will not succeed in drawing two marbles whose total value is equal to 7. The students therefore place their token on the boat. Each student then picks a marble from a different bag. They notice that one of the marbles drawn is blue (2) and the other is orange (5). Since their total value is equal to 7 and this result is not what they predicted, the students put their token back on Zoe Island and wait for the next round. If they had drawn a red marble (1) and a green marble (3), the students would not have obtained a total of 7, which would have corresponded to their prediction. They could then have placed their token on the next island.
Once all teams have completed the game, facilitate a discussion about the strategies used. For example, students might indicate that there were few possibilities for making the last mathematical sentence true (? + ? = 12) and that it was therefore preferable to choose to place the token on the boat.
Source : translated from Guide d’enseignement efficace des mathématiques, de la maternelle à la 3e année, Traitement des données et probabilité, p. 193-194.
