GEEM - Situation d’apprentissage

D1. Littératie statistique :

Traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne.

Situation d'apprentissage : une activité pleine de rebondissements

Durée totale : environ 1h30

Sommaire

Dans cette situation d’apprentissage, les élèves utilisent un diagramme à bandes doubles pour comparer des données primaires et des données secondaires.

Attente	Contenus d'apprentissage
D1. Littératie statistique : Traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne.	D1.2 Collecter des données provenant de sources primaires et secondaires pour répondre à des questions d’intérêt concernant la comparaison entre deux ou plusieurs ensembles de données et organiser ces données à l’aide de tableaux de fréquences et de diagrammes à tiges et à feuilles. D1.3 Choisir le diagramme le plus approprié pour représenter divers ensembles de données à partir d’une variété de diagrammes, y compris des diagrammes à bandes multiples; représenter ces données à l’aide de diagrammes comprenant des sources, des titres, des étiquettes et des échelles appropriés; et justifier son choix. D1.5 Déterminer la moyenne, la médiane et le ou les modes de divers ensembles de données représentées à l’aide de nombres naturels, et expliquer ce que chacune de ces valeurs indique au sujet des données. D1.6 Examiner divers ensembles de données présentées de différentes façons, y compris dans des diagrammes à tiges et à feuilles et des diagrammes à bandes multiples, en se posant des questions au sujet des données, en y répondant et en tirant des conclusions, et ensuite formuler des arguments persuasifs et prendre des décisions éclairées.

Attente

Contenus d'apprentissage

D1. Littératie statistique : Traiter, analyser et utiliser des données pour formuler des arguments persuasifs et prendre des décisions éclairées dans divers contextes de la vie quotidienne.

D1.2 Collecter des données provenant de sources primaires et secondaires pour répondre à des questions d’intérêt concernant la comparaison entre deux ou plusieurs ensembles de données et organiser ces données à l’aide de tableaux de fréquences et de diagrammes à tiges et à feuilles.

D1.3 Choisir le diagramme le plus approprié pour représenter divers ensembles de données à partir d’une variété de diagrammes, y compris des diagrammes à bandes multiples; représenter ces données à l’aide de diagrammes comprenant des sources, des titres, des étiquettes et des échelles appropriés; et justifier son choix.

D1.5 Déterminer la moyenne, la médiane et le ou les modes de divers ensembles de données représentées à l’aide de nombres naturels, et expliquer ce que chacune de ces valeurs indique au sujet des données.

D1.6 Examiner divers ensembles de données présentées de différentes façons, y compris dans des diagrammes à tiges et à feuilles et des diagrammes à bandes multiples, en se posant des questions au sujet des données, en y répondant et en tirant des conclusions, et ensuite formuler des arguments persuasifs et prendre des décisions éclairées.

Intention pédagogique

Cette situation d’apprentissage a pour but d’amener les élèves :

à analyser les données contenues dans un diagramme ou un tableau de fréquences et à en tirer des conclusions;
à effectuer une expérience dans le but de recueillir des données primaires;
à représenter et à communiquer avec efficacité et précision la comparaison entre des données primaires et des données secondaires;
à appliquer des stratégies de résolution de problèmes.

Contexte	Préalables
Au cours des années précédentes, les élèves ont traité des données et ont vu l’importance de bien représenter ces données pour pouvoir les interpréter correctement. Au cours d’activités, elles et ils ont utilisé diverses représentations des données, comme le tableau des fréquences, le diagramme à pictogrammes et le diagramme à bandes. En 4^e année, les élèves consolident leurs connaissances de ces représentations et apprennent à utiliser le diagramme à bandes multiples pour représenter et comparer des données.	La présente situation d’apprentissage expose les élèves, dans un contexte d’une expérience, à la comparaison entre des données secondaires et des données primaires à l’aide, notamment, d’un diagramme à bandes doubles. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent : connaître les composantes d’un diagramme à bandes; savoir utiliser un ruban à mesurer.

Contexte

Préalables

Au cours des années précédentes, les élèves ont traité des données et ont vu l’importance de bien représenter ces données pour pouvoir les interpréter correctement. Au cours d’activités, elles et ils ont utilisé diverses représentations des données, comme le tableau des fréquences, le diagramme à pictogrammes et le diagramme à bandes. En 4^e année, les élèves consolident leurs connaissances de ces représentations et apprennent à utiliser le diagramme à bandes multiples pour représenter et comparer des données.

La présente situation d’apprentissage expose les élèves, dans un contexte d’une expérience, à la comparaison entre des données secondaires et des données primaires à l’aide, notamment, d’un diagramme à bandes doubles. Pour être en mesure de réaliser cette situation d’apprentissage, les élèves doivent :

connaître les composantes d’un diagramme à bandes;
savoir utiliser un ruban à mesurer.

Matériel

annexe 5.1 et annexe 5.3
balles de tennis de table (une par équipe)
rubans à mesurer (un par équipe)
ruban-cache
papier quadrillé de grand format (une feuille par équipe)
marqueurs de couleur différente (deux par équipe)

Vocabulaire mathématique

diagramme à bandes, diagramme à bandes doubles, légende, étiquette, échelle, tableau de fréquences, données primaires, données secondaires, mode

Avant l’apprentissage (mise en train)

Durée : environ 20 minutes

Note : Cette activité peut se réaliser dans la salle de classe, à l’extérieur, dans un corridor ou dans le gymnase.

Présenter aux élèves la mise en situation suivante :

Une entreprise de fabrication est en train de mettre au point une nouvelle balle, la Bondiballe. Selon ses inventeurs, cette balle rebondit très facilement. Persuadée que cette caractéristique nous intéressera, l’entreprise nous a fait parvenir des données à cet effet à l’aide du diagramme que voici. (Présenter l’annexe 5.1.)

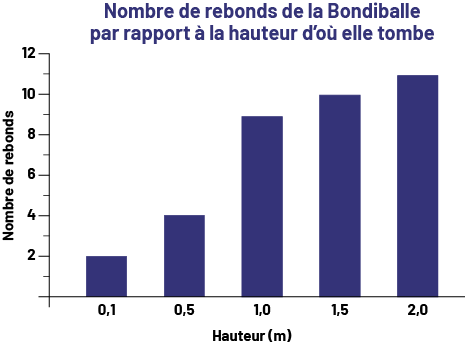
Le diagramme à cinq bandes violettes s’intitule : « Nombre de rebonds de la Bondiballe par rapport à la hauteur d’où elle tombe ». L’axe horizontal se nomme « Hauteur en mètres » tandis que l’axe vertical se nomme « Nombre de rebonds ». La bande située à zéro virgule un sur l’axe horizontal monte jusqu’à deux sur l’axe vertical. La bande située à zéro virgule cinq monte jusqu’à 4. La bande située à un monte jusqu’à 9. La bande située à un virgule cinq monte jusqu’à dix. Et la bande située à deux monte jusqu’à 11.

Demander aux élèves d’indiquer les renseignements qui sont communiqués au moyen de ce diagramme. Leur donner quelques minutes pour qu’elles et ils puissent observer et analyser les données présentées.

Après avoir recueilli un certain nombre d’observations, poursuivre avec la mise en situation :

Convaincue que leur nouvelle balle est celle qui rebondit le mieux, l’entreprise nous suggère de comparer les rebonds de la Bondiballe avec les rebonds d’une autre balle. Je propose qu’on relève leur défi et qu’on utilise une balle de tennis de table. D’après vous, laquelle des deux rebondira le plus et pourquoi?

Accepter les hypothèses des élèves, puis leur suggérer d’effectuer une expérience pour les vérifier. Afin de les aider à planifier la collecte de données, poser des questions telles que :

Comment pourrait-on procéder pour obtenir les résultats avec la balle de tennis de table? (On pourrait laisser tomber une balle de tennis de table et compter les rebonds.)
D’après vous, comment devrions-nous procéder pour que notre comparaison soit valable? (Il faudrait laisser tomber la balle des mêmes hauteurs que celles indiquées dans le diagramme relatif à la Bondiballe.)
Quels moyens pouvons-nous prendre pour nous assurer de faire preuve de rigueur au moment de la collecte de données? (Nous devons nous assurer de laisser tomber la balle sans lui donner d’élan. Il faudrait aussi faire l’expérience plusieurs fois afin d’assurer la validité des résultats.)

Dire aux élèves qu’elles et ils effectueront l’expérience en équipe. Préciser que chaque équipe laissera tomber dix fois une balle de tennis de table à partir d’une hauteur assignée et devra noter, à chaque essai, le nombre de rebonds qu’effectue la balle. Modeler ensuite la marche à suivre au moment de l’expérience :

se rendre à une station de travail avec une balle de tennis de table, du ruban-cache et un ruban à mesurer;
indiquer sur le mur, à l’aide d’un morceau de ruban-cache, une des hauteurs qui sera assignée (par exemple, 2 m);
sans appliquer de force, laisser tomber la balle à partir de la hauteur qu’indique le ruban-cache;
compter le nombre de rebonds en même temps que les élèves et l’inscrire sur une feuille de papier (préciser ce qui constitue un rebond et le moment où l’on doit cesser de compter les rebonds).

Répéter à quelques reprises les deux dernières étapes. Souligner que l’objectif de l’expérience est d’obtenir, pour la balle de tennis de table, des données comparables aux données fournies par l’entreprise et qu’il faudra trouver une représentation de ces données qui facilite la comparaison.

Pendant l’apprentissage (exploration)

Durée : environ 50 minutes

Former des équipes. Assigner à chacune des équipes une station de travail et une des cinq hauteurs (0,1 m, 0,5 m, 1 m, 1,5 m ou 2 m) à partir de laquelle elle devra réaliser l’expérience, en s’assurant d’assigner chaque hauteur à deux équipes différentes.

Rappeler aux élèves que, pour assurer la fiabilité des résultats, chaque équipe doit effectuer 10 essais. Leur suggérer de déterminer d’abord une façon de noter et d’enregistrer les résultats de leur expérience, c’est-à-dire le nombre de rebonds que fait la balle à chaque essai. Leur remettre ensuite une balle de tennis de table, du ruban-cache et un ruban à mesurer.

Allouer suffisamment de temps pour permettre à toutes les équipes de réaliser l’expérience. Circuler et observer le travail des élèves. Intervenir, au besoin, en posant des questions telles que :

Comment procédez-vous pour enregistrer vos résultats?
Les résultats vous surprennent-ils? Pourquoi?
Pourquoi avez-vous opté pour ce type de tableau?

Observations possibles	Interventions possibles
Une équipe éprouve de la difficulté à compter correctement le nombre de rebonds.	Revoir ce que constitue un rebond. Leur suggérer de compter les rebonds à voix haute et d’inscrire systématiquement chaque résultat dans un tableau.
Une équipe manque de rigueur au moment du comptage des rebonds.	Modeler de nouveau les deux dernières étapes de la marche à suivre. Insister sur l’importance de faire preuve de rigueur afin d’obtenir des résultats valables.

Observations possibles

Interventions possibles

Une équipe éprouve de la difficulté à compter correctement le nombre de rebonds.

Revoir ce que constitue un rebond.

Leur suggérer de compter les rebonds à voix haute et d’inscrire systématiquement chaque résultat dans un tableau.

Une équipe manque de rigueur au moment du comptage des rebonds.

Modeler de nouveau les deux dernières étapes de la marche à suivre.

Insister sur l’importance de faire preuve de rigueur afin d’obtenir des résultats valables.

Demander à chaque équipe d’inscrire les résultats de leur expérience dans un tableau des résultats.

Tableau des résultats

Équipe	Hauteur (m)	Nombre de rebonds de la balle de tennis de table
1
2
3
4
5
6
7
8
9
10

Lorsque toutes les équipes ont inscrit leurs résultats, présenter le tableau des résultats. En groupe-classe, demander aux élèves de proposer, pour chacune des hauteurs, une valeur qui représenterait le mieux le nombre de rebonds que fait la balle de tennis de table. Amener les élèves à reconnaître que le résultat le plus fréquent serait une valeur appropriée et qu’on appelle ce résultat le mode d’un ensemble des données. Demander aux élèves de déterminer le mode des données correspondant à chacune des hauteurs et d’inscrire ces résultats dans un tableau de fréquences. Une fois le tableau de fréquences rempli, poser la question suivante : «Quel diagramme nous permettrait de comparer, pour chacune des hauteurs, le nombre de rebonds de la Bondiballe et ceux de la balle de tennis de table?» Laisser les élèves présenter leurs suggestions.

Montrer l’annexe 5.3 qui présente le diagramme à bandes du fabricant de la Bondiballe (diagramme 1) ainsi qu’un diagramme à bandes doubles (diagramme 2). Inviter les élèves à comparer les deux types de diagrammes et à en faire ressortir les ressemblances et les différences. Par exemple, le diagramme à bandes doubles a les mêmes composantes que le diagramme à bandes, soit :

un titre (Sports préférés des élèves de 5^e année);
une étiquette sur chacun des axes (Nombre d’élèves, Sports);
une échelle verticale appropriée (intervalles de deux);
des bandes de même largeur;
un même écart entre les bandes;
la désignation des catégories (hockey, basket-ball, soccer, football, autres).

Par contre, le diagramme à bandes doubles comprend :

deux bandes de couleur différente par catégorie (une bande jaune et une bande rouge);
une légende qui indique ce que représente chaque couleur (les bandes jaunes représentent les données pour les filles et les bandes rouges, les données pour les garçons).

Amener les élèves à constater que le diagramme à bandes doubles permet de comparer facilement des résultats, de les interpréter et d’en tirer des conclusions.

Demander aux élèves de reformer les équipes et remettre à chacune une feuille de papier quadrillé de grand format et deux marqueurs de couleur différente. Demander à chaque équipe de créer un diagramme à bandes doubles pour représenter les données du tableau de fréquences (nombre de rebonds obtenus avec la Bondiballe et ceux obtenus avec la balle de tennis de table).

Laisser le temps aux élèves de compléter leur diagramme. Circuler et, au besoin, aider les élèves en posant des questions telles que :

Est-ce que les bandes sont de la même largeur?
Y a-t-il le même écart entre les bandes doubles?
Que représentent les bandes jaunes? les bandes vertes?
Quel titre porte votre diagramme?
Pouvez-vous me montrer la bande qui indique le nombre de rebonds effectués par la Bondiballe lorsqu’elle tombe d’une hauteur de 1,5 mètre?

Après l’apprentissage (objectivation/échange mathématique)

Durée : environ 15 minutes

Inviter quelques équipes à présenter leur diagramme à la classe et à l’expliquer. Laisser les autres élèves intervenir, tout en leur demandant de justifier leurs propos et leurs questions. Au besoin, poser des questions telles que :

Ce diagramme est-il correctement conçu?
Que représente cette bande?
Est-ce que tous les diagrammes présentés sont identiques? Sinon, en quoi sont-ils différents?

Discuter des résultats de cette expérience en posant des questions telles que :

Pourquoi n’avez-vous pas toutes et tous obtenu les mêmes résultats au cours de l’expérience?
En général, arrivez-vous à la même conclusion?
Pouvez-vous justifier la validité de l’expérience menée?
D’après vos résultats, est-ce qu’on peut déterminer quelle balle rebondit le plus haut? Comment pourrait-on le vérifier? (Puisque l’expérience ne consistait pas à mesurer la hauteur des rebonds, on ne peut déterminer la balle qui rebondit le plus haut. Pour le faire, il faudrait obtenir des données du fabricant relatives à la hauteur du rebond de la Bondiballe et faire ensuite une expérience afin d’obtenir des données comparables avec celles de la balle de tennis de table.)

Amener les élèves à reconnaître l’utilité du diagramme à bandes doubles dans cette situation et à formuler des conclusions. Par exemple :

D’après le diagramme à bandes doubles, on peut reconnaître que plus les balles tombent de haut, plus le nombre de rebonds est élevé.
La balle de tennis de table fait plus de rebonds que la Bondiballe.

Différenciation pédagogique

L’activité peut être modifiée pour répondre aux différents besoins des élèves.

Pour faciliter la tâche	Pour enrichir la tâche
Éliminer de l’expérience les hauteurs de 0,1 m et 0,5 m.	demander aux élèves d’effectuer la même expérience avec d’autres types de balles (par exemple, balle de tennis, balle de golf); inviter les élèves à créer le diagramme à bandes doubles à l’aide d’un logiciel.

Suivi à la maison

Apporter en classe une pile de courrier de diverses provenances et présenter la mise en situation suivante :

Quand j’arrive à la maison en fin de journée, je ramasse mon courrier. J’ai pris l’habitude de le trier selon deux catégories : les lettres et les dépliants publicitaires. (Modeler le triage avec le courrier apporté.) Vos parents font peut-être la même chose avec le contenu de votre boîte aux lettres. L’autre jour, alors que je faisais le tri, deux questions me sont venues à l’esprit :

En général, est-ce qu’on reçoit plus de lettres ou plus de dépliants publicitaires?
Est-ce que le nombre dans chaque catégorie varie selon la journée de la semaine?

Suggérer aux élèves de vous aider à obtenir des réponses à ces questions en prenant part à une enquête. Leur demander de vérifier chaque soir pendant une semaine le courrier reçu à la maison et de noter le nombre de lettres et de dépliants publicitaires qu’il contient. S’assurer que toutes et tous comprennent bien la tâche à effectuer.

Chaque lendemain, déterminer avec les élèves le nombre total de documents reçus par l’ensemble de la classe dans chacune des deux catégories et inscrire ces données dans un tableau de fréquences comme le tableau suivant.

Exemple

Jour	Nombre de lettres	Nombre de dépliants publicitaires
Lundi	68	84
Mardi
Mercredi
Jeudi
Vendredi

À quelques reprises pendant la semaine, inciter les élèves à analyser les données en posant des questions telles que :

Y avait-il plus de lettres ou de dépliants publicitaires hier?
Jusqu’à maintenant, dans quelle catégorie avons-nous enregistré le plus grand nombre d’articles?
À partir des données recueillies jusqu’à maintenant, êtes-vous en mesure de prédire si, à la fin de la semaine, les dépliants publicitaires représenteront plus de la moitié ou moins de la moitié du courrier reçu?

Lorsque toutes les données ont été recueillies, demander aux élèves de prendre en note les données inscrites dans le tableau de fréquences, de représenter ces données au moyen d’un diagramme à bandes et de répondre aux deux questions à l’origine de l’enquête. Analyser les diagrammes et les réponses aux questions en groupe-classe.

Variante

Conserver les données recueillies et répéter l’expérience à un autre moment dans l’année (par exemple, à l’approche d’une fête, du congé d’hiver). Il serait alors possible de comparer les deux ensembles de données, d’en tirer d’autres conclusions et d’établir des liens intéressants.

Source : Guide d’enseignement efficace des mathématiques, de la 4^e à la 6^e année, p. 207-216.