D1.2 Collecter des données qualitatives et des données quantitatives discrètes et continues pour répondre à des questions d’intérêt portant sur une population, et organiser les ensembles de données de façon appropriée, y compris à l’aide d’intervalles.
HABILETÉ : COLLECTER DES DONNÉES
La planification et la réalisation d’une collecte de données permettent de recueillir des données significatives.
Le processus d’enquête est une démarche globale qui comprend quatre étapes, soit cerner la situation, faire une collecte de données, organiser les données et interpréter les résultats.
Une fois que les élèves ont clarifié le problème et formulé une ou plusieurs questions d’intérêts, elles et ils doivent planifier et réaliser une collecte de données. Il est important de tenir compte, au moment de la planification de la collecte de données, des différents types d’enquêtes, des diverses sortes de données et de la différence entre la population et l’échantillon. En faisant participer les élèves activement à la planification de la collecte de données, on les incite à faire des choix réfléchis et à poser un regard critique sur l’ensemble du processus d’enquête.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 44.
Pistes de questionnement
Il importe de donner aux élèves différentes occasions de planifier une collecte de données. C’est en interrogeant les élèves tout au long de cette étape que le personnel enseignant les aide à mieux comprendre l’importance de bien choisir le type d’enquête et la sorte de données qui se prêtent le mieux à la question d’intérêt posée, ainsi que de bien cerner la population et, au besoin, l’échantillon qui sont visés par l’enquête. Ce faisant, il aide les élèves à développer leur sens d’analyse critique, lequel sera très utile à la quatrième étape du processus d’enquête.
Voici quelques idées de questions que le personnel enseignant peut utiliser pour guider les élèves au cours de la planification de la collecte de données.
Le type d’enquête :
Quel type d’enquête se prête le mieux à votre question d’intérêt? Pourquoi?
La sorte de données :
- Quelle sorte de données comptez-vous recueillir?
- Cette sorte de données se prête-t-elle bien à votre question d’intérêt? Pourquoi?
- Si vous comptez utiliser des données secondaires, d’où proviendront-elles? Cette source est-elle fiable?
La population cible :
- Quelle est votre population cible?
- Est-ce bien le groupe qui est visé par votre enquête?
- Votre enquête sera-t-elle menée auprès de la population en entier ou auprès d’une partie de la population seulement?
La taille de l’échantillon :
- Quelle sera la taille de votre échantillon? Comment l’avez-vous déterminée?
- Avec un échantillon de cette taille, les résultats seront-ils représentatifs de la population visée? Pourquoi?
- D’après vous, les résultats seraient-ils semblables si la taille de l’échantillon était plus petite? plus grande? Pourquoi?
La composition de l’échantillon :
- La composition de l’échantillon est-elle exempte de biais?
- Comment allez-vous procéder pour choisir votre échantillon de façon aléatoire?
- Votre échantillon a-t-il besoin d’être stratifié? Pourquoi?
- Quelles strates comptez-vous utiliser dans la composition de votre échantillon et quelle sera la taille de chacune?
Les modalités (où, quand, comment) :
- Où allez-vous mener votre enquête?
- Quand allez-vous mener votre enquête? Pourquoi est-ce un temps propice? Si elle était menée à un autre temps, les résultats seraient-ils les mêmes?
- Comment allez-vous procéder pour obtenir les données recherchées?
- De quelle façon allez-vous enregistrer les résultats de votre enquête?
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 57-58.
HABILETÉ : ORGANISER DES DONNÉES
L’organisation des données et leur représentation au moyen de tableaux et de diagrammes permettent de communiquer des renseignements en vue de leur interprétation. Une fois que les élèves ont cerné la situation et ont recueilli des données, elles et ils doivent organiser les données.
Pourquoi organiser les données
Gal (2002, p. 1-25) indique que l’on organise des données obtenues dans le cadre d’une enquête pour mieux les analyser ou pour communiquer des renseignements. L’objectif de l’enquête étant de trouver une réponse à une ou à plusieurs questions d’intérêts, il est très difficile de fonder cette réponse sur des données qui sont présentées de façon désordonnée. En organisant les données recueillies, on peut les présenter de façon à les résumer, à mettre en évidence certains renseignements qu’elles recèlent, à communiquer leurs principales caractéristiques et à faciliter leur interprétation.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 62.
CONNAISSANCE : TYPES D’ENQUÊTES
Enquête au moyen d’observations
Dans une enquête au moyen d’observations, on enregistre ce que l’on voit ou ce que l’on fait.
Exemples
- On compte le nombre d’oiseaux que l’on voit dans la cour d’école à des moments précis.
- On note le nombre de voitures qui passent à un carrefour pendant un intervalle de temps donné.
- On compte le nombre de fois où l’on se rend au centre sportif dans un mois.
- On note, tous les jours pendant une semaine, l’heure à laquelle on se couche et celle à laquelle on se lève.
Dans la planification d’une enquête au moyen d’observations, il faut prévoir où, quand, quoi et parfois comment observer (par exemple, comment on distingue une voiture qui fait un arrêt incomplet à une intersection d’une voiture qui ne fait aucun arrêt). On peut aussi prévoir si toutes les observations seront faites par une même personne ou si elles seront faites par plusieurs personnes en même temps pour assurer une meilleure fiabilité.
Enquête au moyen d’un prélèvement de mesures
Dans une enquête au moyen d’un prélèvement de mesures, on effectue des mesures simples dans des situations qui ne nécessitent pas une attention spéciale à diverses variables, comme c’est le cas au moment d’une expérience.
Exemples
- On mesure la taille de personnes et la longueur de leur pied pour déterminer s’il y a un lien entre les deux variables.
- On mesure le temps requis par les élèves de la 4e année pour lire un texte donné.
- On mesure la quantité de pluie (en mm) qui tombe chaque jour du mois de mai.
Dans la planification d’une enquête au moyen d’un prélèvement de mesures, il faut prévoir où, quand et comment effectuer les prélèvements. On peut aussi prévoir si toutes les mesures seront prélevées par une même personne ou si elles le seront par plusieurs personnes en même temps pour assurer une meilleure fiabilité.
Enquête au moyen d’une expérience
Dans une enquête au moyen d’une expérience, les données proviennent d’une activité de manipulation à caractère scientifique qui nécessite le respect de certains paramètres préétablis et, souvent, l’utilisation de techniques et d’outils de mesure précis.
Exemples
- À intervalles précis, on mesure la croissance de plantes dont certaines ont reçu une petite quantité d’éléments nutritifs, certaines en ont reçu une quantité plus importante et d’autres n’en ont reçu aucune, et ce, dans le but de voir si les éléments nutritifs contribuent à la croissance des plantes de façon importante.
- Toutes les 30 secondes, on prélève la température d’un liquide quelconque qui a été chauffé à 100 °C et qu’on laisse refroidir. On répète l’expérience avec divers liquides dans le but de comparer la vitesse à laquelle ils refroidissent.
Dans la planification d’une enquête au moyen d’une expérience, il faut faire appel à la démarche scientifique et assurer la fiabilité de la méthode de collecte de données. Il faut aussi contrôler et neutraliser les variables qui pourraient rendre les résultats non valides.
Enquête au moyen d’un sondage
Dans une enquête au moyen d’un sondage, les données sont recueillies en interrogeant un certain nombre d’individus sur un sujet particulier. Les questions posées prennent souvent la forme d’un questionnaire auquel on peut répondre par écrit ou de vive voix.
Exemples
- On demande aux élèves de la classe le nombre d’heures qu’elles et ils passent devant la télévision chaque semaine.
- On demande aux élèves de la 6e année leur genre de musique préféré.
Dans la planification d’une enquête au moyen d’un sondage, il est important de bien rédiger les questions du sondage pour s’assurer qu’elles sont claires et objectives. Il est aussi important de prévoir les réponses qui peuvent être données et parfois de les grouper en catégories.
Enquête au moyen d’une recherche de données existantes
Dans une enquête au moyen d’une recherche de données existantes, les données se trouvent habituellement dans une banque de données électronique (par exemple, site Internet) ou dans un document imprimé (par exemple, livre, magazine, encyclopédie).
Exemples
- On veut comparer la population des provinces et des territoires canadiens.
- On veut comparer les préférences des élèves canadiens de 5 à 7 ans et de 8 à 10 ans quant aux matières scolaires.
Dans la planification d’une enquête au moyen d’une recherche de données existantes, il faut vérifier si ces données sont disponibles, savoir où et comment les obtenir et s’assurer que leur source est fiable.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 46-48.
CONNAISSANCE : QUESTION D’INTÉRÊT
Question autosélectionnée pour laquelle des données doivent être collectées. La question peut non seulement traiter de préférence, mais aussi de grandeur, de quantité ou d’information générale.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : SOURCE PRIMAIRE
Les données primaires sont des données qui sont recueillies par la personne qui mène l’enquête. Elles conviennent bien à l’étude de questions qui touchent des objets et des personnes de l’environnement immédiat des élèves. En effet, elles sont idéales pour initier les élèves au traitement des données puisqu’en général, celles-ci et ceux-ci s’intéressent davantage aux données qu’elles et ils ont recueillies elles-mêmes et eux-mêmes.
Lorsque les élèves connaissent la gamme de réponses possibles, elles et ils peuvent faciliter l’enregistrement des données en utilisant un tableau de fréquences. Prenons, par exemple, une situation de sondage au cours de laquelle on tente de déterminer la sorte de soupe préférée d’une population déterminée. Les élèves peuvent inscrire, dans un tableau comme celui ci-dessous, un trait dans la rangée correspondant à chacune des réponses données. Cette stratégie de dénombrement est appelée pointage. Chaque cinquième trait est tracé obliquement sur les quatre traits précédents, ce qui permet par la suite de compter plus facilement les résultats. La colonne Fréquence indique le nombre total de traits dans chaque rangée.
Soupes préférées
| Sorte | Dénombrement | Fréquence |
|---|---|---|
| Soupe au poulet et aux nouilles |  |
7 |
| Potage au brocoli |  |
4 |
| Crème de champignons | 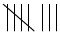 |
8 |
| Soupe aux légumes | 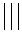 |
3 |
| Soupe aux tomates | 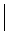 |
1 |
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 50-51.
CONNAISSANCE : SOURCE SECONDAIRE
Les données secondaires sont des données qui ont été recueillies par une personne ou un organisme (par exemple, chercheuse ou chercheur, entreprise, association) autre que la personne qui mène l’enquête. On trouve ces données dans des livres, des encyclopédies, des magazines, des journaux, ainsi que dans Internet. Elles sont particulièrement utiles pour répondre à des questions d’intérêts pour lesquelles il est difficile ou impossible de recueillir des données primaires (par exemple, au fil des ans, à combien se chiffrait la population francophone dans les principales grandes villes canadiennes?). Elles peuvent aussi servir à interpréter d’autres données avec lesquelles elles sont mises en relation. Le personnel enseignant doit aider les élèves à développer leur aptitude à juger de la pertinence des données secondaires auxquelles elles et ils sont exposés quotidiennement. Pour ce faire, il doit continuellement les sensibiliser à l’importance de vérifier la fiabilité des diverses sources d’information, ainsi qu’à l’importance de faire un usage judicieux des données présentées. Les diagrammes et les données qui paraissent dans les journaux procurent un contexte authentique et signifiant pour traiter des données.
Processus d’enquête et Internet
L’accès au Web donne l’occasion aux élèves de participer à des projets d’envergure nationale et même internationale qui les placent en situation authentique de collecte et de partage de données, favorisant ainsi la collaboration entre élèves de divers pays.
Par exemple, le projet Recensement à l’école « est un projet international en ligne qui permet aux élèves de la 4e année à la 12e année de découvrir le monde des enquêtes et de la statistique. Ce projet a pris naissance au Royaume-Uni en 2000, et des écoles d’Australie, du Canada, de la Nouvelle-Zélande et d’Afrique du Sud y prennent maintenant part. Des jeunes de ces pays remplissent de façon anonyme un questionnaire en classe. Ils fournissent des renseignements non confidentiels comme leur taille, la durée du trajet entre la maison et l’école, et leur matière préférée. Les réponses sont intégrées dans une base de données nationale, qui sera ensuite ajoutée à une base de données internationale maintenue au Royaume-Uni*. »
Puisque les élèves doivent reconnaître la différence entre des données primaires et des données secondaires à partir de la 4e année, de tels projets représentent des outils intéressants pour mener une enquête sur un sujet qui les intéresse et les touche plus particulièrement.
* Tiré de Statistique Canada, Recensement à l’école – Canada!
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 51-52.
CONNAISSANCE : POPULATION
En statistique, l’ensemble des objets, des événements ou des personnes que l’on veut étudier est appelé population. Au moment de la planification de la collecte de données, il faut d’abord définir la population cible de l’enquête, c’est-à-dire le groupe de personnes ou d’objets visé par l’enquête. Le choix de la population est en partie dicté par l’intention de l’enquête et l’énoncé de la question d’intérêt.
Exemples de populations en statistique
- les habitantes et habitants du Canada;
- les amatrices et amateurs de baseball;
- les élèves de la 4e année de l’école;
- les élèves du cycle primaire;
- les parents des élèves du cycle moyen.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 52.
CONNAISSANCE : TECHNIQUES D’ÉCHANTILLONNAGE
Processus de sélection
Échantillonnage aléatoire simple
Les élèves doivent comprendre qu’une des meilleures façons d’avoir un bon échantillon libre de biais est de le choisir de façon aléatoire, c’est-à-dire de façon que toutes et tous les membres de la population aient les mêmes chances d’en faire partie.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 55.
Échantillonnage aléatoire systématique
L’échantillonnage aléatoire systématique est utilisé lorsque les sujets d’une population sont sélectionnés selon une approche systématique qui a été déterminée de manière aléatoire. Par exemple, un échantillon pourrait être déterminé à partir d’une liste alphabétique de noms, en utilisant un nom de départ et un nombre (par exemple, un nom sur quatre) qui sont sélectionnés au hasard.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Processus de stratification
Dans certaines enquêtes, on pourrait vouloir s’assurer que certains sous-groupes de la population sont bien représentés dans l’échantillon (par exemple, le sous-groupe des élèves du cycle primaire et celui des élèves du cycle moyen). On dit alors que la population est stratifiée (divisée en groupes mutuellement exclusifs) et on veut que chaque strate (groupe) soit représentée dans l’échantillon.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 56.
Échantillonnage aléatoire stratifié
L’échantillonnage aléatoire stratifié consiste à diviser la population en strates, puis à prélever un échantillon aléatoire de chacune. Par exemple, une population scolaire pourrait être divisée en deux sous-populations (strates) : l’une avec les élèves qui prennent l’autobus pour aller à l’école et l’autre avec celles et ceux qui ne le font pas. Ensuite, un sondage pourrait être mené auprès de 10 % de la population choisie au hasard dans chacune de ces strates.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
