D1.2 Collect qualitative data and discrete and continuous quantitative data to answer questions of interest about a population, and organize the sets of data as appropriate, including using intervals.
Skill: Collecting Data
Planning and conducting data collection provides meaningful data.
The inquiry process is a comprehensive one that involves four steps: identifying the situation, collecting the data, organizing the data, and interpreting the results.
Once students have clarified the problem and formulated one or more questions of interest, they should plan and carry out a data collection. It is important to consider the different types of inquiry, the different kinds of data, and the difference between the population and the sample when planning the data collection. Involving students actively in the planning of the data collection encourages them to make thoughtful choices and to look critically at the entire inquiry process.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 44.
Lines of Questioning
It is important to provide students with a variety of opportunities to plan a data collection. By interviewing students throughout this stage, educators help them to better understand the importance of choosing the type of inquiry and the type of data that are most appropriate for the question of interest, as well as identifying the population and, if necessary, the sample to be surveyed. In doing so, it helps students develop critical thinking skills, which will be very useful in the fourth step of the inquiry process.
Here are some ideas for questions that teachers can use to guide students through the data collection planning process.
Type of Inquiry:
What type of inquiry is most appropriate for your question of interest? Why?
The Type of Data:
- What kind of data will you collect?
- Does this kind of data lend itself well to your question of interest? Why or why not?
- If you are going to use secondary data, where will it come from? Is this source reliable?
Target Population:
- What is your target population?
- Is this the group that is the focus of your investigation?
- Will your inquiry be conducted with the entire population or only a portion of the population?
Sample Size:
- What will your sample size be? How did you determine it?
- With a sample of this size, will the results be representative of the target population? Why or why not?
- Do you think the results would be similar if the sample size were smaller? larger? why?
Sample Composition:
- Is the sample composition free of bias?. Convince me.
- How will you go about selecting your sample at random?
- Does your random sample need to be stratifed? Why or why not?
- What strata do you plan to use in your sample composition and what will be the size of each stratum?
Modalities (Where, When, How):
- Where will you conduct your inquiry?
- When are you going to conduct your inquiry? Why is this a good time? If it were conducted at another time, would the results be the same?
- How will you go about getting the data you need?
- How will you record the results of your inquiry?
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 57-58.
Skill: Organizing Data
Organizing data and representing it in tables and graphs helps communicate information for interpretation. Once students have identified the situation and collected data, they need to organize the data.
Why Organize Data
Gal (2002) indicates that data obtained in an inquiry is organized for further analysis or to communicate information. Since the purpose of the inquiry is to find an answer to one or more questions of interest, it is very difficult to base that answer on data that is presented in a disorganized fashion. By organizing the data collected, we can present it in a way that summarizes it, highlights certain information it contains, communicates its main characteristics, and facilitates its interpretation.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 62.
Knowledge: Types of Inquiry
Data Collection by Observation
In data collection by observation, one records what one sees or does.
Examples
- We count the number of birds we see in the schoolyard at specific times.
- We count the number of cars passing through an intersection during a given time interval.
- We count the number of times we go to the sports center in a month.
- Every day for a week, we note the time we go to bed and the time we get up.
In planning data collection by observation, it is necessary to plan where, when, what, and sometimes how to observe (for example, how to distinguish between a car that makes an incomplete stop at an intersection and a car that makes no stop). It is also possible to plan whether all observations will be made by one person or whether they will be made by several people at the same time to ensure better reliability.
Data Collection by Means of Taking Measurements
When collecting data by taking measurements, measurements are taken in situations that involve a limited number of variables, as is the case in an experiment.
Examples
- We measure people's height and foot length to see if there is a connection between the two variables.
- We measure the time it takes Grade 4 students to read a given text.
- We measure the amount of rain (in mm) that falls each day in May.
When planning to collect data by measurement, it is important to consider where, when and how to collect the measurements, and whether all measurements will be collected by one person or by several people at the same time to ensure greater reliability.
Data Collection by Means of an Experiment
When performing an experiment, data is collected from a scientific activity that requires adherence to certain preset parameters and, often, the use of precise measurement techniques and tools.
Examples
- At specific intervals, we measure the growth of plants, some of which have received a small amount of nutrients, some of which have received a larger amount, and some of which have not received any, to see if nutrients contribute significantly to plant growth.
- Every 30 seconds, the temperature of any liquid that has been heated to 100°C and left to cool down. The experiment is repeated with different liquids to compare the rate at which they cool.
In planning an experiment, the scientific approach must be used and the reliability of the data collection method must be ensured. Variables that may render the results invalid must be controlled and neutralized.
Survey
When conducting a survey, data is collected by asking a number of individuals about a particular topic. The questions often take the form of a questionnaire that can be answered in writing or orally.
Examples
- Students in the class are asked how many hours they spend watching television each week.
- Grade 6 students are asked what kind of music they prefer.
In planning a survey, it is important to write the survey questions well to ensure that they are clear and objective. It is also important to anticipate the responses that may be given and sometimes to group them into categories.
Secondary Data Collection
In secondary data collection, the data is usually found in an electronic database (for example, website) or in a printed document (for example, book, magazine, encyclopedia).
Examples
- We want to compare the population of the provinces and territories of Canada.
- We want to compare the school subject preferences of Canadian students aged 5 to 7 and 8 to 10.
When planning secondary data collection, it is important to check whether the data is available, where and how to obtain it, and to ensure that the source is reliable.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 46-48.
Knowledge: Question of Interest
A question of interest is a self-selected question for which data must be collected. The question may deal not only with preference, but also with magnitude, quantity, or general information.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Knowledge: Primary Source
Primary data is data that is collected by the person conducting the inquiry. It is well suited to the study of issues that involve objects and people in the students' immediate environment. In fact, they are ideal for introducing students to data management since students are generally more interested in the data they have collected themselves.
Once students know the range of possible responses, they can facilitate the recording of data by using a frequency table. For example, in a a survey situation where a population is asked to identify the preferred type of soup of a given population, students can record a tally in the row corresponding to each response in a table such as the one below. This counting strategy is called tallying. Each fifth tally is drawn at an angle to the previous four tallies, making it easier to count the results later. The Frequency column shows the total number of tallies in each row.
Favourite Soups
| Type | Counting | Frequency |
|---|---|---|
| Chicken Noodle Soup |  |
7 |
| Broccoli Soup |  |
4 |
| Cream of Mushroom Soup | 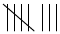 |
8 |
| Vegetable Soup |  |
3 |
| Tomato Soup | 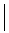 |
1 |
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 50-51.
Knowledge: Secondary Source
Secondary data is data that has been collected by a person or organization (for example, researcher, company, association) other than the person conducting the inquiry. This data can be found in books, encyclopedias, magazines, newspapers, as well as on the Internet. It is particularly useful for answering questions of interest for which it is difficult or impossible to collect primary data (for example, what was the size of the Francophone population in Canada's major cities in recent years?). Data can also be used to interpret other data with which they are related. Since students are exposed to secondary data on a daily basis, teachers should help students develop their ability to judge its reliability, validity, and relevance. This can be accomplished by continually educating students about the importance of checking the reliability of various sources of information, and the importance of making good use of the data presented. Graphs and data that appear in newspapers provide authentic and meaningful context for dealing with data.
Inquiry Process and the Internet
Access to the Web provides opportunities for students to participate in national and even international projects that place them in authentic data collecting and sharing situations, thus fostering collaboration among students from different countries.
For example, the Census at School project "is an international online project that introduces students in grade 4 to 12 to the world of surveys and statistics. The project began in the United Kingdom in 2000, and schools in Australia, Canada, New Zealand, and South Africa are now taking part. Students in each participating country anonymously fill in an online questionnaire in class. They answer non-confidential questions about topics such as their height, travel time to and from school, and favourite subject. The responses become part of a national database, which is later added to an international database that is maintained in the United Kingdom.
Since students are expected to recognize the difference between primary and secondary data by Grade 4, such projects are valuable tools for conducting a survey on a topic of particular interest and concern to them.
* Taken from Statistics Canada, Census at School – Canada!
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 51-52.
Knowledge: Population
In statistics, the set of objects, events, or people that we want to study is called a population. When planning data collection, the target population for the inquiry must be defined. The choice of population is partly dictated by the inquiry intent and the statement of the question of interest.
Examples of Populations in Statistics
- the people of Canada;
- baseball fans;
- the school's Grade 4 students;
- elementary school students;
- parents of students in grades 4 to 6.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 52.
Knowledge: Sampling Techniques
Selection Process
Simple Random Sampling
Students should understand that one of the best ways to have a good bias-free sample is to choose it randomly, that is, so that all members of the population have an equal chance of being included.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 55.
Systematic Random Sampling
Systematic random sampling is used when subjects from a population are selected using a systematic approach that has been determined at random. For example, a sample could be determined from an alphabetical list of names, using a starting name and a number (for example, every fourth name) that are randomly selected.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
Stratification Process
In some inquiries, one might want to ensure that certain subgroups of the population are well represented in the sample (for example, the subgroup of primary grade students and the subgroup of junior grade students). We then say that the population is stratified (divided into mutually exclusive groups) and we want each stratum (group) to be represented in the sample.
Source: translated from Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, Traitement des données et probabilité, p. 56.
Stratified Random Sampling
Stratified random sampling involves dividing the population into strata and then taking a random sample from each stratum. For example, a school population could be divided into two sub-populations (strata): one with students who take the bus to school and one with those who do not. Then, a survey could be conducted with 10% of the randomly selected population in each of these strata.
Source: The Ontario Curriculum. Mathematics, Grades 1-8 Ontario Ministry of Education, 2020.
