D1.2 Collecter des données qualitatives et des données quantitatives discrètes et continues pour répondre à des questions d’intérêt, et organiser les ensembles de données de façon appropriée, y compris en utilisant des pourcentages.
HABILETÉ : RÉPONDRE À DES QUESTIONS D’INTÉRÊT
Au cours de la planification de leur enquête ou de leur expérience de probabilité, les élèves doivent d’abord s’assurer de bien cerner la situation. Pour ce faire, elles et ils doivent clarifier le problème et formuler une ou plusieurs questions auxquelles il est possible de répondre en s’appuyant sur des données. Elles et ils doivent également tenir compte, dans la mesure du possible, de certains facteurs de variabilité qui peuvent influer sur les résultats de l’enquête ou de l’expérience.
Clarifier le problème
Avant de procéder à la résolution d’une situation-problème, le personnel enseignant doit s’assurer que le problème est bien compris de toutes et de tous les élèves. Il peut vérifier cette compréhension et, au besoin, les aider à clarifier le problème en animant un échange d’idées au sujet de ladite situation.
Formuler des questions
Une fois que les élèves comprennent bien ce qu’elles et ils cherchent ou ce qu’elles et ils voudraient savoir, elles et ils peuvent commencer à planifier l’enquête. Les élèves doivent, dans un premier temps, formuler clairement la question d’intérêt, c’est-à-dire la question qui vient préciser l’intention de l’enquête. Une question d’intérêt est une question à laquelle il est possible de répondre qu’à partir de données variables. Ainsi, « Combien d’enfants y a-t-il dans ta famille? » n’est pas une question d’intérêt, puisque la réponse est déterminée (par exemple, trois enfants) et qu’elle ne dépend pas de données variables. Cependant, « Combien d’enfants par famille y a-t-il chez les élèves du groupe-classe? » est une question d’intérêt, puisque pour y répondre, il faut d’abord recueillir des données relatives au nombre d’enfants dans chacune des familles des élèves. À la lumière des réponses obtenues, il sera alors possible de conclure, par exemple, que dans la majorité des familles des élèves, il y a deux enfants.
Le personnel enseignant doit aider les élèves à comprendre l’importance de bien formuler la question d’intérêt et de s’assurer qu’elle reflète correctement ce qu’elles et ils cherchent. Les élèves doivent aussi apprendre à reconnaître que le choix de la question d’intérêt a une incidence sur le type d’enquête qui devrait ensuite être effectué. Voici quelques exemples de questions d’intérêt que les élèves pourraient aborder. Chaque question est accompagnée du type d’enquête qu’elle suggère.
| Question d'intérêt | Type d'enquête |
|---|---|
| Quelles sont les trois variétés de pommes préférées des élèves de la classe de Mme Pomerleau? | Enquête au moyen d’un sondage |
| Combien de portions de légumes et de fruits les élèves du groupe-classe mangent-elles et mangent-ils dans une journée? | Enquête au moyen d'observations |
| Quelle est la taille des élèves du groupe-classe? | Enquête au moyen de mesures |
| Combien de rebonds fait une balle de tennis de table lorsqu'on la laisse tomber d’une hauteur de un mètre? | Enquête au moyen d’une expérience scientifique |
| Si on laisse tomber un verre de styromousse, est-il plus probable qu'il atterrisse à l'endroit, à l'envers ou sur le côté? | Enquête au moyen d’une expérience de probabilité |
| Quel est le mois de l'année au cours duquel les précipitations sont les plus abondantes? | Enquête au moyen de données existantes |
Source : Guide d’enseignement efficace des mathématiques de la 1re à la 3e année, p. 59-61.
HABILETÉ : COLLECTER DES DONNÉES
La planification d’une collecte de données et sa réalisation permettent de recueillir des données significatives.
Le processus d’enquête est une démarche globale qui comprend quatre étapes, soit cerner la situation, faire une collecte de données, organiser les données et interpréter les résultats.
Une fois que les élèves ont clarifié le problème et formulé une ou plusieurs questions d’intérêt, elles et ils doivent planifier et réaliser une collecte de données. Il est important de tenir compte, au moment de la planification de la collecte de données, des différents types d’enquêtes, des différentes sortes de données et de la différence entre la population et l’échantillon. En faisant participer les élèves activement à la planification de la collecte de données, cela les incite à faire des choix réfléchis et à poser un regard critique sur l’ensemble du processus d’enquête.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 44.
Pistes de questionnement
Il importe de donner aux élèves différentes occasions de planifier une collecte de données. C’est en posant des questions aux élèves tout le long de cette étape que le personnel enseignant les aide à mieux comprendre l’importance de bien choisir le type d’enquête et le type de données qui se prêtent le mieux à la question d’intérêt posée, puis à bien identifier la population et, au besoin, l’échantillon visés par l’enquête. Ce faisant, il aide les élèves à développer leur sens d’analyse critique, lequel sera très utile au cours de la quatrième étape du processus d’enquête.
Le personnel enseignant peut utiliser les idées de questions ci-dessous pour guider les élèves au cours de la planification de la collecte de données.
Le type d’enquête :
Quel type d’enquête se prête le mieux à votre question d’intérêt? Pourquoi?
La sorte de données :
- Quelle sorte de données comptez-vous recueillir?
- Cette sorte de données se prête-t-elle bien à votre question d’intérêt? Pourquoi?
- Si vous comptez utiliser des données secondaires, d’où proviendront-elles? Cette source est-elle fiable?
La population cible :
- Quelle est votre population cible?
- Est-ce bien le groupe que vise votre enquête?
- Votre enquête sera-t-elle menée auprès de la population en entier ou auprès d’une partie de la population seulement?
La taille de l’échantillon :
- Quelle sera la taille de votre échantillon? Comment l’avez-vous déterminée?
- Avec un échantillon de cette taille, les résultats seront-ils représentatifs de la population visée? Pourquoi?
- D’après vous, les résultats seraient-ils semblables si la taille de l’échantillon était plus petite? plus grande? Pourquoi?
La composition de l’échantillon :
- La composition de l’échantillon est-elle exempte de biais?
- Comment allez-vous procéder pour choisir votre échantillon de façon aléatoire?
- Votre échantillon a-t-il besoin d’être stratifié? Pourquoi?
- Quelles strates comptez-vous utiliser dans la composition de votre échantillon? Quelle sera la taille de chacune?
Les modalités (où, quand, comment) :
- Où allez-vous mener votre enquête?
- Quand allez-vous mener votre enquête? Pourquoi est-ce un temps propice? Si elle était menée à un autre moment, les résultats seraient-ils les mêmes?
- Comment allez-vous procéder pour obtenir les données recherchées?
- De quelle façon allez-vous enregistrer les résultats de votre enquête?
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 57-58.
HABILETÉ : ORGANISER DES DONNÉES
L’organisation des données et leur représentation par des tableaux et des diagrammes aident à communiquer des renseignements en vue de leur interprétation. Une fois que les élèves ont cerné la situation et ont recueilli des données, elles et ils doivent les organiser.
Pourquoi organiser les données
Gal (2002, p. 1-25) indique que nous organisons les données obtenues dans le cadre d’une enquête pour mieux les analyser ou pour communiquer des renseignements. L’objectif de l’enquête étant de trouver une réponse à une ou à plusieurs questions d’intérêt, il est très difficile de fonder cette réponse sur des données qui sont présentées de façon désordonnée. En organisant les données recueillies, on peut les présenter de façon à les résumer, à mettre en évidence certains renseignements, à communiquer leurs principales caractéristiques et à faciliter leur interprétation.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 62.
CONNAISSANCE : TYPE D’ENQUÊTE
Enquête au moyen d’observations
Dans une enquête au moyen d’observations, nous enregistrons ce que nous voyons ou ce que nous faisons.
Exemples
- Nous comptons le nombre d’oiseaux que nous voyons dans la cour de l’école à des moments précis.
- Nous notons le nombre de voitures qui passent à un carrefour pendant un intervalle de temps donné.
- Nous comptons le nombre de fois où nous nous rendons au centre sportif dans un mois.
- Nous notons, tous les jours, pendant une semaine, l’heure à laquelle nous nous couchons et l’heure à laquelle nous nous levons.
Dans la planification d’une enquête au moyen d’observations, il faut prévoir où, quand, quoi et, parfois, comment observer; par exemple, comment distinguer une voiture qui fait un arrêt incomplet à une intersection d’une voiture qui ne fait aucun arrêt. Il est aussi possible de déterminer si toutes les observations seront faites par une seule et même personne ou par plusieurs personnes en même temps pour assurer une meilleure fiabilité.
Enquête au moyen d’un prélèvement de mesures
Dans une enquête au moyen d’un prélèvement de mesures, nous effectuons des mesures simples dans des situations qui ne nécessitent pas une attention spéciale à diverses variables, comme c’est le cas au cours d’une expérience.
Exemples
- Nous mesurons la taille de personnes et la longueur de leur pied pour déterminer s’il y a un lien entre ces deux variables.
- Nous mesurons le temps requis pour les élèves de 7e année pour lire un texte donné.
- Nous mesurons la quantité de pluie (en mm) qui tombe chaque jour du mois de mai.
Dans la planification d’une enquête au moyen d’un prélèvement de mesures, il faut prévoir où, quand et comment effectuer les prélèvements. Il est aussi possible de déterminer si toutes les mesures seront prélevées par une seule et même personne ou par plusieurs personnes en même temps pour assurer une meilleure fiabilité.
Enquête au moyen d’une expérience
Dans une enquête au moyen d’une expérience, les données proviennent d’une activité de manipulation à caractère scientifique qui nécessite le respect de certains paramètres préétablis et, souvent, l’utilisation de techniques et d’outils de mesure précis.
Exemples
- À intervalles précis, nous mesurons la croissance de plantes, dont certaines ont reçu une petite quantité d’éléments nutritifs, d’autres, une quantité plus importante, et d’autres encore qui n’en ont reçu aucune, et ce, en vue de voir si les éléments nutritifs contribuent à la croissance des plantes de façon importante.
- Toutes les 30 secondes, nous prélevons la température d’un liquide quelconque qui a été chauffé à 100 °C et que nous laissons refroidir. Nous répétons l’expérience avec divers liquides en vue de comparer la vitesse à laquelle ils refroidissent.
Dans la planification d’une enquête au moyen d’une expérience, il faut faire appel à la démarche scientifique et assurer la fiabilité de la méthode de collecte de données. Il faut aussi contrôler et neutraliser les variables qui pourraient rendre les résultats non valides.
Enquête au moyen d’un sondage
Dans une enquête au moyen d’un sondage, les données sont recueillies en interrogeant un certain nombre d’individus sur un sujet particulier. Les questions posées prennent souvent la forme d’un questionnaire auquel nous pouvons répondre par écrit ou de vive voix.
Exemples
- Nous demandons aux élèves du groupe-classe le nombre d’heures qu’elles et ils passent devant la télévision chaque semaine.
- Nous demandons aux élèves de 7e année le genre de musique qu’elles et ils préfèrent.
Dans la planification d’une enquête au moyen d’un sondage, il est important de bien rédiger les questions du sondage pour s’assurer qu’elles sont claires et objectives. Il est aussi important de déterminer les réponses qui peuvent être données et, parfois, de les regrouper en catégories.
Enquête au moyen d’une recherche de données existantes
Dans une enquête au moyen d’une recherche de données existantes, les données se trouvent habituellement dans une banque de données électronique, comme un site Web, ou dans un document imprimé, comme un livre, un magazine ou une encyclopédie.
Exemples
- Nous voulons comparer la population des provinces et des territoires du Canada.
- Nous voulons comparer les préférences des élèves du cycle moyen avec celles des élèves du cycle intermédiaire de la province relativement aux matières scolaires.
Dans la planification d’une enquête au moyen d’une recherche de données existantes, il faut vérifier si ces données sont disponibles, savoir où et comment les obtenir et s’assurer que leur source est fiable.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 46-48.
CONNAISSANCE : TECHNIQUES D’ÉCHANTILLONNAGE
Processus de sélection
Échantillonnage aléatoire simple
Les élèves doivent comprendre qu’une des meilleures façons d’avoir un bon échantillon libre de biais est de le choisir de façon aléatoire, c’est-à-dire de façon que tous les individus aient les mêmes chances d’en faire partie.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 55.
Échantillonnage aléatoire systématique
L’échantillonnage aléatoire systématique est utilisé lorsque les sujets d’une population sont sélectionnés selon une approche systématique qui a été déterminée de manière aléatoire; par exemple, un échantillon pourrait être déterminé en partant d’une liste alphabétique de noms, en utilisant un nom de départ et un nombre, par exemple, un nom sur quatre, sélectionné au hasard.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Processus de stratification
Dans certaines enquêtes, nous pourrions vouloir nous assurer que certains sous-groupes de la population sont bien représentés dans l’échantillon; par exemple, le sous-groupe des élèves du cycle moyen et celui des élèves du cycle intermédiaire. La population est donc stratifiée, c’est-à-dire qu’elle est divisée en groupes mutuellement exclusifs. Chaque strate (groupe) doit être représentée dans l’échantillon.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 56.
Échantillonnage aléatoire stratifié
L’échantillonnage aléatoire stratifié consiste à diviser la population en strates, puis à prélever un échantillon aléatoire de chacune; par exemple, une population scolaire pourrait être divisée en deux sous-populations (strates) : l’une avec les élèves qui prennent l’autobus pour aller à l’école et l’autre avec celles et ceux qui ne le font pas. Un sondage pourrait ensuite être mené auprès de 10 % de la population choisie au hasard dans chacune de ces strates.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
CONNAISSANCE : SORTE DE DONNÉES
Il existe plusieurs types de données, et chacun peut avoir une influence sur la façon de les recueillir et de les organiser. À partir du cycle moyen, les élèves doivent comprendre la différence entre les données qualitatives et les données quantitatives, de même qu’entre les données primaires et les données secondaires. Cette compréhension fait en sorte qu’elles et ils peuvent déterminer le type de données qu’elles et ils comptent utiliser pour les besoins de l’enquête et planifier leur collecte en conséquence.
Données qualitatives et données quantitatives
Les données qualitatives sont représentées par des mots; par exemple, si, pour déterminer la répartition des anniversaires de naissance des élèves selon les saisons, nous procédons en posant la question « À quelle saison ton anniversaire de naissance a-t-il lieu? », les quatre réponses qualitatives seraient printemps, été, automne ou hiver. À la question « Quels sont tes loisirs préférés? », les réponses devraient être des noms d’activités. Dans ce cas, toutefois, si nous déterminons un trop grand nombre de réponses différentes en raison de la diversité des activités possibles, nous pouvons utiliser des catégories, comme des activités culturelles, sportives ou de détente. Les données qualitatives sont souvent représentées par un diagramme à bandes et, au cycle intermédiaire, plutôt par un diagramme circulaire.
Exemple
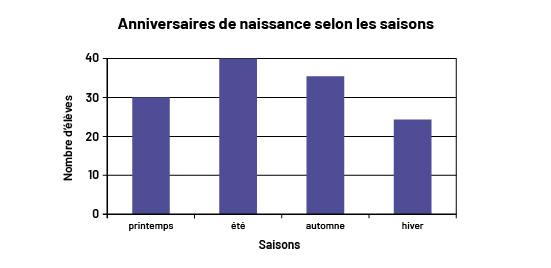
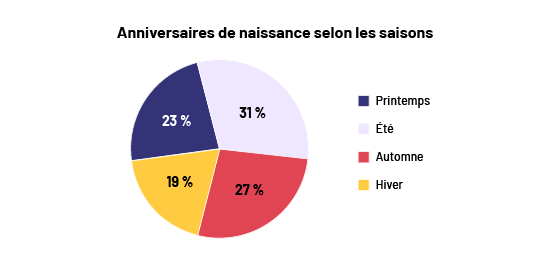
Les données quantitatives sont représentées par des nombres; par exemple, à la question « Quelle est la hauteur de la plante à la fin de chaque semaine? », la réponse devrait être quantitative, par exemple, 5 cm, 15 cm. Si nous déterminons un trop grand nombre de réponses différentes, nous pouvons utiliser des intervalles; par exemple, si nous mesurons la longueur des pieds des élèves du groupe-classe, nous pouvons regrouper les données selon des intervalles de 15 cm à 15,9 cm ou de 16 cm à 16,9 cm. Les données quantitatives sont souvent représentées par un diagramme à ligne brisée ou un diagramme à tiges et à feuilles.
Exemple
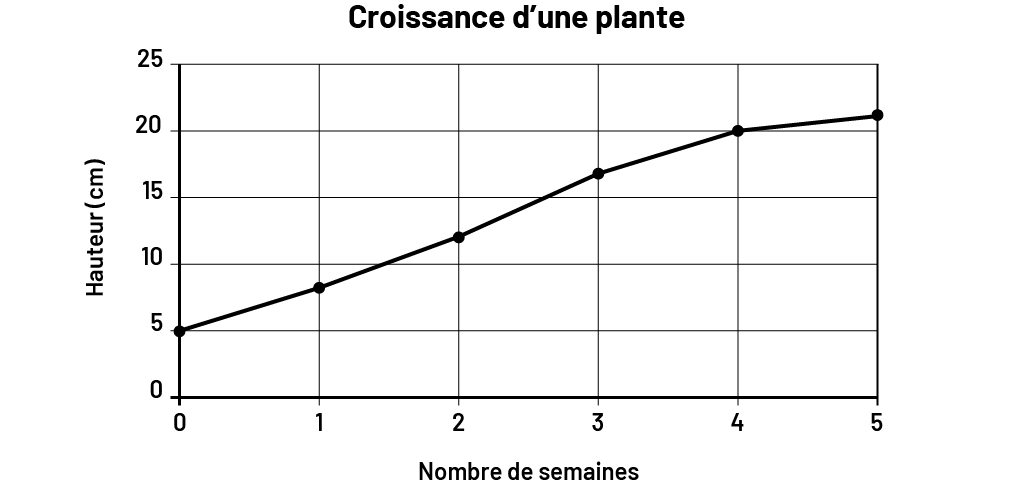 Image Le diagramme à ligne brisée s’intitule « Croissance d’une plante ». L’axe
horizontal se nomme « Nombre de semaines » et est gradué de zéro à cinq. L’axe vertical se nomme « Hauteur en
centimètres » et est gradué de zéro à 25. Le premier point est situé à zéro sur l’axe horizontal et à cinq sur l’axe
vertical. Le deuxième point est situé à un sur l’axe horizontal et entre cinq et dix sur l’axe vertical. Le
troisième point est situé à deux sur l’axe horizontal et entre dix et 15 sur l’axe vertical. Le quatrième point est
situé à trois sur l’axe horizontal et entre 15 et 20 sur l’axe vertical. Le cinquième point est situé à quatre sur
l’axe horizontal et à 20 sur l’axe vertical. Et le sixième point est situé à cinq sur l’axe horizontal et légèrement
au-dessus de 20 sur l’axe vertical.
Image Le diagramme à ligne brisée s’intitule « Croissance d’une plante ». L’axe
horizontal se nomme « Nombre de semaines » et est gradué de zéro à cinq. L’axe vertical se nomme « Hauteur en
centimètres » et est gradué de zéro à 25. Le premier point est situé à zéro sur l’axe horizontal et à cinq sur l’axe
vertical. Le deuxième point est situé à un sur l’axe horizontal et entre cinq et dix sur l’axe vertical. Le
troisième point est situé à deux sur l’axe horizontal et entre dix et 15 sur l’axe vertical. Le quatrième point est
situé à trois sur l’axe horizontal et entre 15 et 20 sur l’axe vertical. Le cinquième point est situé à quatre sur
l’axe horizontal et à 20 sur l’axe vertical. Et le sixième point est situé à cinq sur l’axe horizontal et légèrement
au-dessus de 20 sur l’axe vertical.
Longeur, en centimètres, des pieds des élèves de 7e année
| 15, | 7 8 8 9 |
| 16, | 3 5 6 7 7 9 |
| 17, | 0 3 6 7 8 8 9 |
| 18, | 0 0 1 3 3 3 5 6 6 9 9 |
| 19, | 1 2 2 4 4 4 4 5 |
| 20, | 1 2 4 4 5 |
| 21, | 1 3 |
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 49-50.
Les données quantitatives peuvent être discrètes ou continues.
Données discrètes
Données qui peuvent être comptées.
Exemple
Le nombre de billets vendus pour match de soccer.
Données continues
Données qui peuvent prendre n’importe quelle valeur à l’intérieur d’un intervalle choisi.
Exemple
La vitesse d’une athlète lors d’une course de 200 m ou la température de l’eau sur la cuisinière.
Source : En avant, les maths!, 7e année, CM, Données, p. 2.
Données primaires et données secondaires
Les données primaires sont recueillies par la personne qui mène l’enquête. Elles conviennent bien à l’étude de questions qui touchent des objets et des personnes de l’environnement immédiat des élèves. En effet, elles sont idéales pour les initier au traitement des données, puisqu’en général elles et ils s’intéressent davantage aux données qu’elles et ils ont recueillies elles-mêmes et eux-mêmes. Lorsque les élèves connaissent les réponses possibles, elles et ils peuvent faciliter l’enregistrement des données en utilisant un tableau de fréquences.
Les données secondaires sont recueillies par une personne ou un organisme, comme une chercheuse ou un chercheur, une entreprise ou une association, autre que la personne qui mène l’enquête. Ces données se trouvent dans des livres, des encyclopédies, des magazines, des journaux ainsi que dans Internet. Elles sont particulièrement utiles pour répondre à des questions d’intérêt pour lesquelles il est difficile ou impossible de recueillir des données primaires; par exemple, « Au fil des années, à combien se chiffrait la population francophone dans les principales grandes villes canadiennes? ». Elles peuvent aussi servir à interpréter d’autres données avec lesquelles elles sont mises en relation. Les élèves devraient être en mesure de choisir, selon le type d’enquête et la nature de la question d’intérêt posée, si elles et ils auront recours à des données primaires ou à des données secondaires.
Le personnel enseignant doit aider les élèves à développer leur aptitude à juger de la pertinence des données secondaires auxquelles elles et ils sont exposés quotidiennement. Pour ce faire, il doit continuellement les sensibiliser à l’importance de vérifier la fiabilité des diverses sources d’information ainsi qu’à l’importance de faire un usage judicieux des données présentées.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 50-52.
CONNAISSANCE : QUESTION D’INTÉRÊT
Après avoir cerné la situation et déterminé un élément à préciser ou une orientation à prendre, les élèves passent à la formulation de différents types de questions d’intérêt. Cette démarche aide les élèves à reconnaître l’importance de poser de bonnes questions qui ciblent bien la situation proposée.
Konold et Higgins (2001) soutiennent que le premier défi des élèves est de transformer une interrogation en une question d’intérêt. Selon le Guidelines for Assessment and Instruction in Statistics Education (GAISE) Report (Franklin et coll., 2005, p. 11), la formulation d’une question d’intérêt requiert une compréhension de la différence entre une question qui prévoit une réponse déterministe et une autre qui prévoit une réponse fondée sur des données variables; par exemple, la question « Quelle est la couleur de tes cheveux? » n’est pas une question d’intérêt, puisqu’elle demande une réponse précise. Cependant, la question « Quelle est la couleur des cheveux des élèves du groupe-classe? » est une question d’intérêt, puisqu’elle demande une réponse qui variera selon les données obtenues. Une question d’intérêt doit donc mener à une collecte de données pertinentes, à l’enregistrement de ces données et à la création d’outils pour les interpréter.
La formulation de questions d’intérêt aide à préciser l’intention de l’enquête et le type d’enquête qui suivra. Dans le cas d’une enquête au moyen d’un sondage, elle aide aussi à élaborer la ou les questions précises et objectives qui seront posées.
Intention de l’enquête
L’intention de l’enquête ressort habituellement du processus de formulation des questions d’intérêt. De fait, les questions d’intérêt et l’intention de l’enquête se précisent parallèlement, car les questions sont le reflet de l’intention. Chapin et ses collaborateurs (2002, p. 14) décrivent quatre intentions possibles :
- décrire ou résumer un ensemble de données;
- déterminer les préférences ou les opinions en partant d’un ensemble de données;
- comparer deux ensembles de données;
- généraliser en partant des données recueillies et faire des prédictions.
Voici des exemples de mots clés et de questions d’intérêt compatibles avec chacune de ces intentions.
Décrire ou résumer un ensemble de données
Mots clés :
Quelle ou quel…?
Combien…?
Laquelle ou lequel…?
Exemples de questions d’intérêt :
- Quelle taille de police de caractères est utilisée dans les livres de la section des romans policiers de la bibliothèque?
- Combien de voitures font un arrêt complet au coin de la rue?
- Laquelle des classes de 7e année a lu le plus de livres le mois dernier?
Déterminer les préférences ou les opinions en partant d’un ensemble de données
Mots clés :
Quels sont… préférés?
Quelle est la pire…? la meilleure…?
Exemples de questions d’intérêt :
- Quels sont les groupes de musique préférés des élèves du cycle intermédiaire?
- Quelles sont les qualités que recherchent les élèves chez une amie ou un ami?
- Quelle est la meilleure façon d’améliorer ses résultats en mathématiques?
Comparer deux ensembles de données
Mots clés :
Quelles sont les ressemblances entre…?
Y a-t-il une relation entre… et…?
Quel… le mieux? le plus? le moins?
Exemples de questions d’intérêt :
- Quelles sont les ressemblances et les différences entre les sports que pratiquent les élèves de 6e année et ceux que pratiquent les élèves de 7e année?
- Y a-t-il une relation entre le nombre d’heures d’ensoleillement et la croissance d’un plant de tomates?
- Quelle balle rebondit le mieux? La balle de tennis ou la balle de tennis de table?
Généraliser en partant des données recueillies et faire des prédictions
Mots clés :
Peut-on prédire…?
Quel sera…?
Exemples de questions d’intérêt :
- En comparant la longueur des bras et de la taille des élèves, peut-on prédire la taille d’une ou d’un élève de 7e année en mesurant la longueur de ses bras?
- Quelle sera la population de notre ville dans cinq ans?
Questions de sondage
Selon l’expérience et l’année d’études des élèves, le personnel enseignant devrait fournir une aide plus ou moins grande dans la formulation des questions de sondage. Il doit amener les élèves à comprendre l’importance de faire en sorte que ces questions soient compatibles avec la question d’intérêt et l’intention du sondage; par exemple, une question de sondage comme « Combien de sports pratiques-tu? » est incompatible avec la question d’intérêt « Quelles sont les ressemblances et les différences entre les sports que pratiquent les élèves de 6e année et ceux que pratiquent les élèves de 7e année? ». Les élèves doivent reconnaître qu’une question de sondage peut générer un grand nombre de réponses différentes, rendant ainsi la collecte, l’enregistrement et l’interprétation des données plus difficiles. Dans de tels cas, elles et ils doivent apprendre à formuler la question de façon à proposer un nombre limité de réponses, comme une question à choix multiple ou une question avec échelle.
Exemples
- Dans quel pays tes parents sont-ils nés?
Cette question peut générer une grande variété de réponses. Dans certains milieux, il risque même d’y avoir autant de réponses que de personnes ayant répondu au sondage.
Note : On pourrait toutefois choisir de conserver la question, mais d’enregistrer les réponses sous un nombre limité de catégories; par exemple, selon les continents.
- Parmi les activités sportives ci-dessous, laquelle préfères-tu?
- Gymnastique
- Badminton
- Soccer
- Hockey
- Aucune
Cette question à choix multiple présente un nombre limité de réponses parmi lesquelles doivent choisir les personnes répondant au sondage, ce qui facilite l’organisation et l’analyse des données.
- Aimerais-tu visiter un pays autre que le Canada?
- Pas du tout
- Un peu
- Beaucoup
Cette question avec échelle vise à aider les personnes répondant au sondage à situer leur préférence ou leur évaluation sur un continuum selon des catégories déjà établies, ce qui facilite l’organisation et l’analyse des données. Lors de la formulation des questions de sondage, il est important d’inciter les élèves à puiser dans leurs expériences personnelles afin de réfléchir à l’étendue des interprétations et des réponses possibles de leur question, ainsi qu’à l’importance des mots utilisés. Dans certains cas, le personnel enseignant peut leur suggérer de tester leur question auprès d’un groupe de répondantes et répondants pour obtenir un échantillon de réponses. Elles et ils pourront ainsi vérifier si la question génère le genre de réponse attendu et si la réponse est telle qu’il leur sera relativement simple de les organiser et de les interpréter. Selon les résultats, elles et ils pourront décider soit de procéder au sondage, soit de reformuler la question pour corriger une lacune relevée au cours de l’expérience.
Dans certaines situations, les élèves doivent rédiger un questionnaire de sondage comprenant plus d’une question en vue de collecter des données qui seront par la suite analysées, regroupées, comparées et interprétées.
La formulation d’une question de sondage et le choix des réponses suggérées peuvent influer sur les données recueillies et les résultats de l’enquête. C’est ce qui s’appelle un biais. Une question biaisée est dépourvue de l’objectivité requise pour assurer la fiabilité des résultats. Le personnel enseignant doit aider les élèves à comprendre le concept de biais et à le reconnaître dans la formulation d’une question; par exemple, toutes les questions ci-dessous sont plus ou moins biaisées parce qu’elles disent clairement ou laissent sous-entendre qu’il n’y a pas assez de ballons pour les activités à la récréation.
Exemples de questions de sondage biaisées
- Ne croyez-vous pas qu’il manque des ballons pour jouer pendant la récréation?
- Plusieurs élèves du cycle intermédiaire croient qu’il n’y a pas assez de ballons pour les activités pendant la récréation. Êtes-vous d’accord?
- Croyez-vous qu’il manque de ballons pour les activités pendant la récréation et que la direction d’école devrait agir pour régler le problème?
- L’école achètera 15 ballons pour les activités pendant la récréation. Combien de ballons l’école devrait-elle acheter pour qu’il y en ait assez?
Dans cette situation, une question objective ou non biaisée pourrait être la suivante :
- Le nombre de ballons disponibles pour les activités pendant la récréation est-il suffisant?
Qu’est-ce qu’un biais?
Un biais dans un sondage est un type d’erreur qui favorise ou défavorise une réponse en particulier et qui fait en sorte que les résultats du sondage ne sont pas fiables.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 32-37.
CONNAISSANCE : TABLEAU DE FRÉQUENCES RELATIVES
Un tableau de fréquences relatives présente la fraction, le nombre décimal ou le pourcentage des valeurs de données dans chaque catégorie. La somme des fréquences relatives est 1 ou 100 %.
Source : Curriculum de l'Ontario, Programme-cadre de mathématiques de la 1re à la 8e année, 2020, Ministère de l'Éducation de l'Ontario.
Exemple
Le nombre de réponses par catégorie est exprimé en proportion du nombre total de réponses (600) ainsi qu’en pourcentage.
Type d’actualité que lisent les adolescentes et les adolescents
| Type d’actualité | Fréquence | Fréquence relative (fraction) | Fréquence relative (nombre décimal) | Fréquence relative (%) |
|---|---|---|---|---|
| Enquêtes | 59 | \(\frac{59}{600}\) | 0,10 | 10 % |
| Marchés boursiers | 9 | \(\frac{9}{600}\) | 0,02 | 2 % |
| Sports | 137 | \(\frac{137}{600}\) | 0,23 | 23 % |
| Spectacles et culture | 122 | \(\frac{122}{600}\) | 0,20 | 20 % |
| Monde | 47 | \(\frac{47}{600}\) | 0,08 | 8 % |
| Santé | 32 | \(\frac{32}{600}\) | 0,05 | 5 % |
| Sciences et technologie | 68 | \(\frac{68}{600}\) | 0,11 | 11 % |
| Environnement | 31 | \(\frac{31}{600}\) | 0,05 | 5 % |
| Agriculture et alimentation | 24 | \(\frac{24}{600}\) | 0,04 | 4 % |
| Entreprises | 3 | \(\frac{3}{600}\) | 0,01 | 1 % |
| Nouvelles régionales | 68 | \(\frac{68}{600}\) | 0,11 | 11 % |
| Total | 600 | \(\frac{600}{600}\) | 1 | 100 % |
