D1.6 Examiner divers ensembles de données présentées de différentes façons, y compris à l’aide de diagrammes circulaires et de diagrammes trompeurs, en se posant des questions au sujet des données, en y répondant, en remettant en question des idées reçues et en tirant des conclusions, et ensuite formuler des arguments persuasifs et prendre des décisions éclairées.
HABILETÉ : EXAMINER ET ANALYSER DES DONNÉES REPRÉSENTÉES DANS DIVERS DIAGRAMMES, Y COMPRIS DES DIAGRAMMES CIRCULAIRES ET DES DIAGRAMMES TROMPEURS
L’habileté à interpréter des résultats est liée à l’habileté à raisonner dans la mesure où elle exige une certaine capacité de réflexion et d’analyse. Le personnel enseignant doit aider les élèves à développer cette habileté en leur proposant diverses activités qui portent sur l’interprétation des résultats et en posant des questions qui incitent les élèves à examiner ces résultats de près. Ce faisant, le personnel enseignant contribuera aussi au développement chez les élèves de compétences en matière de littératie statistique.
Gal (2002, p. 1-25) suggère que l’interprétation des résultats se fasse selon deux points de vue, soit celui de l’enquêteuse ou de l’enquêteur et celui de la lectrice ou du lecteur. Du point de vue de l’enquêteuse ou de l’enquêteur, les élèves examinent des données qu’elles et ils ont recueillies dans le cadre d’une enquête et qu’elles et ils ont résumées dans des diagrammes ou des tableaux. Elles et ils les interprètent ensuite pour répondre à la question d’intérêt qu’elles et ils ont posée au début de l’enquête. Du point de vue de la lectrice ou du lecteur, les élèves examinent des données qui proviennent de l’extérieur, c’est-à-dire qui ont été colligées par d’autres. Dans ce contexte, le personnel enseignant peut en profiter pour leur présenter des données liées à d’autres matières; par exemple, sciences et technologie, études sociales, éducation physique et santé.
Lorsque le personnel enseignant présente un tableau ou un diagramme aux élèves, il importe de leur accorder suffisamment de temps de réflexion pour qu’elles et ils examinent les données et s’en fassent une idée générale. La réflexion peut se faire individuellement ou en petits groupes. Le personnel enseignant devrait ensuite poser des questions ouvertes pour aider les élèves à communiquer leurs observations et leurs idées dans leurs propres mots et à élaborer des idées à partir de celles de leurs pairs; par exemple, elle ou il pourrait leur poser les questions suivantes :
- Que remarquez-vous au sujet de ce diagramme?
- Qu’est-ce que ce diagramme présente d’intéressant?
- Que pouvez-vous dire au sujet de ces données?
- Que pouvez-vous dire au sujet de ce diagramme?
Ces questions ouvertes suscitent une diversité de réponses, de sorte que tous les élèves peuvent communiquer de façon générale leurs observations, leurs descriptions et leurs conclusions. Par la suite, le personnel enseignant peut poser des questions plus précises afin d’aider les élèves à développer l’habileté à attribuer un sens aux données. En traitement des données, cette habileté implique trois niveaux de compréhension, soit la lecture des données, l’établissement de liens entre elles et la lecture au-delà des données.
| Niveau de compréhension | Description du niveau |
|---|---|
| Lecture des données | Cerner les données telles qu'elles sont représentées par le tableau ou le diagramme. |
| Établissement de liens entre les données | Comparer et combiner certaines données afin d'établir des relations entre elles. |
| Lecture au-delà des données | Inférer ou prédire des renseignements implicites ou explicites tirés d'un diagramme ou d'un tableau et émettre des conclusions. |
Le personnel enseignant s’attarde parfois surtout au premier niveau. Or, selon Friel et ses collaborateurs (2001, p. 124-158), il devrait toujours poser des questions relatives à chacun des trois niveaux de compréhension, et ce, quelles que soient la représentation ou l’organisation des données. C’est de cette façon que les élèves peuvent devenir autonomes dans l’interprétation des diagrammes et des tableaux, ainsi que dans l’utilisation des mesures statistiques.
Une explication plus détaillée de chacun de ces trois niveaux de compréhension est présentée ci-dessous, ainsi que des exemples de questions pertinentes que pourrait poser le personnel enseignant dans le cadre d’une activité d’interprétation des résultats.
Lecture des données
À ce premier niveau de compréhension, les élèves sont en mesure de déterminer :
- les composantes de la représentation, comme le titre du tableau ou du diagramme, l’échelle ou la légende, la désignation des axes et le choix des catégories;
- la valeur de certaines données représentées.
Exemples de questions pertinentes :
- De quoi est-il question dans ce diagramme? (titre)
- Combien de… dans la catégorie? Comment le sait-on?
- Combien y a-t-il de catégories?
- Quelle est l’échelle sur l’axe horizontal?
- Que représente l’axe vertical dans ce diagramme?
- Que représente le plus grand secteur?
Établissement de liens entre les données
Ce niveau de compréhension demande de considérer les données moins comme « […] un amalgame de données personnelles ayant chacune ses propres caractéristiques » que comme « […] un ensemble de données collectives avec de nouvelles propriétés » (Konold et Higgins, 2003, p. 202). Ce niveau est plus difficile à atteindre, car les élèves doivent analyser les données individuelles en les combinant ou en comparant des ensembles de données.
À ce deuxième niveau de compréhension, les élèves sont en mesure :
- de comparer des données en employant des expressions telles que plus que, moins que, autant que, le plus, le moins, un peu plus, trois fois moins, il y a une petite différence entre;
- de comparer les longueurs des bandes dans un diagramme à bandes ou des secteurs d’un diagramme circulaire;
- de faire les liens entre différentes façons de décrire une relation entre des données;
- de combiner certaines données selon certaines catégories et de comparer les fréquences de chacune;
- de décrire certains avantages et désavantages de deux représentations différentes des mêmes données;
- de déterminer la valeur de certaines mesures statistiques (mode, médiane, moyenne) d’un ensemble de données.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 89-93.
Exemple
Voici deux diagrammes circulaires liés aux heures de travail à temps partiel, par semaine, des élèves de deux écoles secondaires de la région. En tout, 690 élèves ont répondu au sondage à l’École secondaire de la Colline et 752 élèves à l’École secondaire des Cygnes.
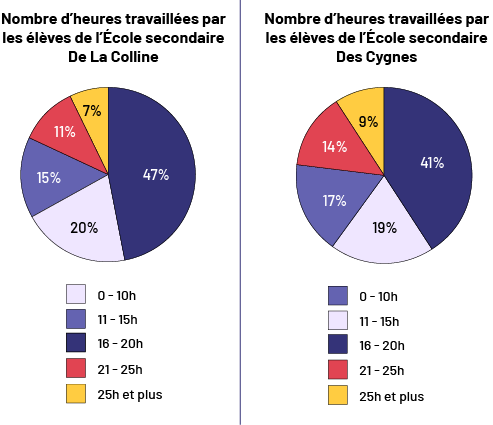 image Deux
diagrammes circulaires sont présentés.Le premier diagramme s’intitule Nombre d’heures travaillées par les élèves de
l’école secondaire De La Colline. Il est divisé en cinq parts. La part de zéro à dix heures fait 20 pourcent, en
violet pâle. La part d’onze à 15 heures fait 15 pourcent, en violet. La part de 16 à 20 heures fait 47 pourcent, en
bleu marine. La part de 21 à 25 heures fait onze pourcent, en rouge. Et la part de 25 heures et plus fait sept
pourcent, en jaune.Le deuxième diagramme s’intitule Nombre d’heures travaillées par les élèves de l’école secondaire
Des Cygnes. Il est divisé en cinq parts. La part de zéro à onze heures fait 17 pourcent, en violet. La part d’onze à
15 heures fait 19 pourcent, en violet pâle. La part de 16 à 20 heures fait 41 pourcent, en bleu marine. La part de 21
à 25 heures fait 14 pourcent, en rouge. Et la part de 25 heures et plus fait neuf pourcent, en jaune.
image Deux
diagrammes circulaires sont présentés.Le premier diagramme s’intitule Nombre d’heures travaillées par les élèves de
l’école secondaire De La Colline. Il est divisé en cinq parts. La part de zéro à dix heures fait 20 pourcent, en
violet pâle. La part d’onze à 15 heures fait 15 pourcent, en violet. La part de 16 à 20 heures fait 47 pourcent, en
bleu marine. La part de 21 à 25 heures fait onze pourcent, en rouge. Et la part de 25 heures et plus fait sept
pourcent, en jaune.Le deuxième diagramme s’intitule Nombre d’heures travaillées par les élèves de l’école secondaire
Des Cygnes. Il est divisé en cinq parts. La part de zéro à onze heures fait 17 pourcent, en violet. La part d’onze à
15 heures fait 19 pourcent, en violet pâle. La part de 16 à 20 heures fait 41 pourcent, en bleu marine. La part de 21
à 25 heures fait 14 pourcent, en rouge. Et la part de 25 heures et plus fait neuf pourcent, en jaune.
Voici des exemples de questions pertinentes à poser aux élèves :
- D’après ce sondage, à quelle école y a-t-il un plus haut pourcentage d’élèves qui travaillent de 11 h à 15 h par semaine? (15 % des élèves de l’École secondaire de la Colline travaillent de 11 h à 15 h par semaine, tandis que 19 % des élèves de l’École secondaire des Cygnes travaillent le même nombre d’heures. Donc, il y a plus d’élèves de l’École secondaire des Cygnes qui travaillent de 11 h à 15 h par semaine.)
- Dans les deux écoles, combien d’élèves travaillent jusqu’à 10 h par semaine? (138 élèves de l’École secondaire de la Colline travaillent jusqu’à 10 h par semaine comparativement à environ 128 élèves de l’École secondaire des Cygnes. Donc, 266 élèves en tout travaillent jusqu’à 10 h par semaine.)
- À l’École secondaire de la Colline, la majorité des élèves travaille combien d’heures par semaine? Qu’en est-il des élèves de l’École secondaire des Cygnes? (À l’École secondaire de la Colline, la majorité des élèves travaille de 16 h à 20 h par semaine. Il en est de même pour les élèves de l’École secondaire des Cygnes.)
- À quelle école les élèves travaillent-elles et travaillent-ils le plus d’heures par semaine? (Puisqu’on parle du nombre d’heures le plus élevé, je regarde la catégorie 25 h et plus. Je vois que 7 % des élèves (environ 48 élèves) de l’École secondaire de la Colline travaillent 25 h et plus contrairement à 9 % des élèves (environ 68 élèves) de l’École secondaire des Cygnes. Il y a donc plus d’élèves de l’École secondaire des Cygnes qui travaillent 25 h et plus par semaine.)
- Observe bien les deux diagrammes circulaires. Qu’est-ce qui pourrait être trompeur dans la comparaison des données? (Je remarque que certaines couleurs ont été utilisées dans les deux diagrammes, mais pas pour les mêmes catégories, ce qui pourrait être trompeur. De plus, le bleu a été utilisé deux fois dans les diagrammes, et les teintes pourraient porter à confusion dans l’interprétation des données. Finalement, il peut être trompeur de se fier strictement aux pourcentages des deux diagrammes pour comparer, puisque la population d’élèves n’est pas la même.)
- D’après toi, pourquoi l’auteure ou l’auteur du sondage a-t-elle ou a-t-il décidé de représenter les données à l’aide d’un diagramme circulaire? (Un diagramme circulaire aide à déterminer la plus grande catégorie ou la plus petite. Nous pouvons estimer le pourcentage qu’occupe chaque secteur selon l’amplitude de l’angle de chacun d’eux. De plus, nous pouvons utiliser les fractions pour décrire les catégories lorsque nous utilisons un diagramme circulaire pour représenter les données; par exemple, dans ce cas-ci, nous pouvons conclure que près de la moitié (\(\frac{1}{2}\)) des élèves de l’École secondaire de la Colline travaillent de 16 h à 20 h par semaine.)
- En analysant le diagramme circulaire de l’École secondaire de la Colline, détermine le mode des données représentées dans celui-ci. (Puisque plus d’élèves travaillent de 16 h à 20 h par semaine, le mode est alors « 16 h à 20 h ». Cette réponse constitue donc la plus populaire chez les élèves qui fréquentent l’École secondaire de la Colline.)
Source : adapté de En avant, les maths!, 7e année, ML, Données, p. 4-6.
Lecture au-delà des données
Bien que la lecture explicite et littérale des données représentées dans un diagramme ou un tableau soit une composante importante de l’habileté à lire des diagrammes, la lectrice ou le lecteur tire le plein potentiel du diagramme lorsqu’elle ou il est capable d’interpréter et de généraliser en partant de ces données (Kirk et coll., 1980, p. 382 [traduction libre]).
À ce troisième niveau de compréhension, les élèves font appel à plusieurs habiletés de la pensée critique et statistique. Elles et ils sont en mesure :
- de reconnaître ce que le diagramme ou le tableau ne « dit pas » directement;
- de préciser la tendance d’un ensemble de données;
- de faire des inférences et des prédictions;
- de tirer des conclusions et de les justifier;
- d’évaluer la crédibilité et la logique des prédictions et des conclusions;
- d’évaluer la représentativité de l’étendue, du mode, de la médiane et de la moyenne;
- de faire un retour sur les étapes du processus d’enquête.
Questions pertinentes :
- Pensez-vous que… est le plus commun dans toutes les villes? Pourquoi?
- Si le sondage est présenté avec d’autres choix de réponse, pensez-vous que les résultats seront semblables?
- Comment organiser les données pour découvrir d’autres renseignements? (par exemple, en regroupant les données des élèves du cycle moyen et celles des élèves du cycle intermédiaire, nous pouvons analyser la préférence des élèves en général)
- Quelles autres questions pouvez-vous poser en partant de ce diagramme?
Source : adapté de Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 96-98.
HABILETÉ : À PARTIR D’UN DIAGRAMME, TIRER DES CONCLUSIONS, FORMULER DES ARGUMENTS ET PRENDRE DES DÉCISIONS
À la suite de l’examen et de l’analyse des données (trois niveaux de compréhension, soit la lecture des données, l’établissement de liens entre elles et la lecture au-delà des données), les élèves sont amenées et amenés à tirer des conclusions, à formuler des arguments et à prendre des décisions.
L’interprétation des résultats aide à tirer des conclusions pertinentes afin de répondre à des questions d’intérêt et de prendre des décisions réfléchies.
« L’étude de la statistique comprend la collecte, l’organisation, la représentation, l’analyse et l’interprétation de données. Ces données sont ensuite utilisées pour prédire, faire des inférences et prendre des décisions. […] Les élèves ont besoin de développer les habiletés qui les aideront à vivre dans une société où les statistiques sont omniprésentes, sans être induites et induits en erreur. Sans ces habiletés, leurs connaissances pour comprendre le monde seront insuffisantes. » [traduction libre]
(Burns, 2000, p. 59)
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 89.
La prise de décision est très importante dans le processus d’enquête, puisque sans prise de décision, le processus perd tout son sens. En effet, pourquoi mettre sur pied une enquête, puis recueillir, organiser et analyser des données si nous n’avons pas l’intention d’en tirer des conclusions? Dans plusieurs cas, la prise de décision se limite à donner une réponse à la question que nous nous posions initialement. Dans d’autres cas, il s’agit d’utiliser cette réponse pour décider si nous devons agir dans tel ou tel sens. Le personnel enseignant doit donc amener les élèves à répondre à la question d’intérêt qui est à l’origine de l’enquête ou à prendre une décision en se basant :
- sur les relations établies entre les données;
- sur le sens des données;
- sur les conclusions qu’en ont tirées les élèves.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 101.
CONNAISSANCE : DIAGRAMME TROMPEUR
Diagramme affichant des renseignements qui faussent les données.
Exemples
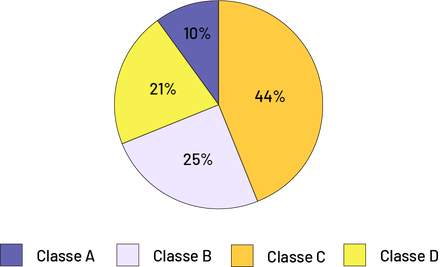 image Le
diagramme circulaire est divisé en quatre parts. La part de la classe « A » est de dix pourcent, en violet. La part de
la classe « B » est de 25 pourcent, en violet pâle. La part de la classe « C » est de 44 pourcent, en orange. Et la
part de la classe « D » est de 21 pourcent, en jaune.
image Le
diagramme circulaire est divisé en quatre parts. La part de la classe « A » est de dix pourcent, en violet. La part de
la classe « B » est de 25 pourcent, en violet pâle. La part de la classe « C » est de 44 pourcent, en orange. Et la
part de la classe « D » est de 21 pourcent, en jaune.
Note : Ce diagramme est trompeur, puisque le jaune a été utilisé deux fois dans le diagramme, et les teintes pourraient porter à confusion dans l’interprétation des données. Au moment de créer un diagramme, il est préférable d’utiliser des couleurs distinctes pour chaque catégorie afin de bien les reconnaître.
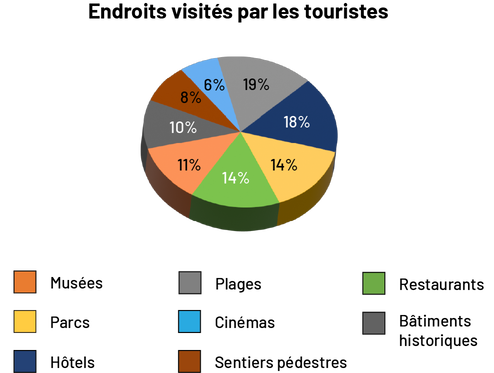 image Le
diagramme circulaire s’intitule Endroits visités par les touristes. Il est divisé en huit parts. La part des musées
fait onze pourcent, en orange. La part des parcs fait 14 pourcent, en jaune. La part des hôtels fait 18 pourcent, en
bleu marine. La part des plages fait 19 pourcent, en gris. La part des cinémas fait six pourcent, en bleu pâle. La
part des sentiers pédestres fait huit pourcent, en marron. La part des restaurants fait 14 pourcent, en vert. Et la
part des bâtiments historiques fait dix pourcent, en gris foncé.
image Le
diagramme circulaire s’intitule Endroits visités par les touristes. Il est divisé en huit parts. La part des musées
fait onze pourcent, en orange. La part des parcs fait 14 pourcent, en jaune. La part des hôtels fait 18 pourcent, en
bleu marine. La part des plages fait 19 pourcent, en gris. La part des cinémas fait six pourcent, en bleu pâle. La
part des sentiers pédestres fait huit pourcent, en marron. La part des restaurants fait 14 pourcent, en vert. Et la
part des bâtiments historiques fait dix pourcent, en gris foncé.
Note : Ce diagramme est trompeur, puisque le pourcentage de personnes qui ont visité des hôtels ou des restaurants semble être le même si l’on se fie uniquement à la taille des portions. Pourtant, 18 % des touristes ont visité un ou des hôtels comparativement à 14 % qui sont allés au restaurant. Une différence de 4 % sépare les deux endroits visités. Cela étant dit, au premier coup d’œil, nous devrions être en mesure de voir qu’un plus grand pourcentage de touristes a visité un ou des hôtels et qu’un plus faible pourcentage de gens est allé dans un ou des restaurants.
Il importe de souligner que, tout le long de l’étape de l’interprétation des résultats, le personnel enseignant doit inciter les élèves à exercer un jugement critique quant aux données présentées afin qu’elles et ils prennent conscience des limites éventuelles de cette interprétation. L’habileté à exercer ce jugement critique constitue une composante importante de la pensée statistique. Pour les aider à développer cette habileté, le personnel enseignant doit les habituer :
- à remettre en question la représentativité et la fiabilité des données primaires ou secondaires en se posant des questions telles que les suivantes : La collecte de données a-t-elle été faite sans biais? La source des données secondaires est-elle fiable?
- à vérifier si la représentation donne un portrait juste des données en se posant des questions telles que la suivante : Les données sont-elles représentées sans laisser de fausses impressions?
Exemple
Le personnel enseignant présente le diagramme ci-dessous tiré d’un magazine commercial.
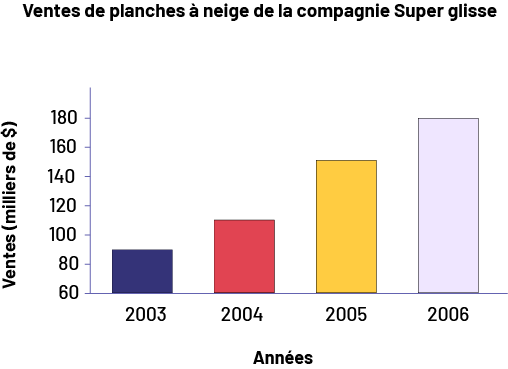 image Le
diagramme à bande s’intitule Ventes de planches à neige de la compagnie Super Glisse. L’axe horizontal correspond aux
années tandis que l’axe vertical, gradué de 60 à 180, correspond aux ventes en milliers de dollars.La bande de 2003,
en bleu marine, s’élève à 90. La bande de 2004, en rouge, s’élève à 110. La bande de 2005, en jaune, s’élève à 150. Et
la bande de 2006, en violet pâle, s’élève à 180.
image Le
diagramme à bande s’intitule Ventes de planches à neige de la compagnie Super Glisse. L’axe horizontal correspond aux
années tandis que l’axe vertical, gradué de 60 à 180, correspond aux ventes en milliers de dollars.La bande de 2003,
en bleu marine, s’élève à 90. La bande de 2004, en rouge, s’élève à 110. La bande de 2005, en jaune, s’élève à 150. Et
la bande de 2006, en violet pâle, s’élève à 180.
Au cours de l’interprétation des résultats, le personnel enseignant incite les élèves à remettre en question la représentation des données en leur disant : « D’après le diagramme, les ventes semblent avoir doublé de 2004 à 2005. Qu’en est-il? » Après analyse, les élèves devraient être en mesure de reconnaître que, même si la bande jaune est deux fois plus longue que la bande rouge, en réalité, les ventes de 2004 sont d’environ 110 000 $ et celles de 2005 sont d’environ 155 000 $; elles n’ont donc pas doublé. Il importe de souligner que ce diagramme n’est pas incorrect en tant que tel, puisqu’il représente les données de façon exacte. Cependant, il peut laisser de fausses impressions et induire en erreur si nous ne l’analysons pas attentivement.
Le personnel enseignant peut ensuite amener les élèves à reconnaître que, pour représenter les données sans induire personne en erreur, il suffirait de graduer l’axe vertical selon une échelle de 0 à 180 comme suit.
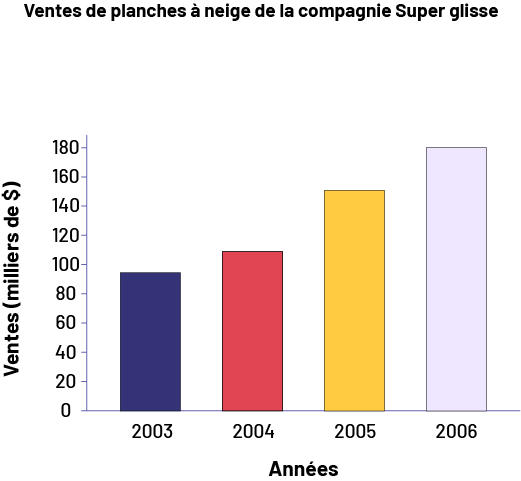 image Le
diagramme à bande s’intitule Ventes de planches à neige de la compagnie Super Glisse. L’axe horizontal correspond aux
années tandis que l’axe vertical, gradué de zéro à 180, correspond aux ventes en milliers de dollars.La bande de 2003,
en bleu marine, s’élève à 90. La bande de 2004, en rouge, s’élève à 110. La bande de 2005, en jaune, s’élève à 150. Et
la bande de 2006, en violet pâle, s’élève à 180.
image Le
diagramme à bande s’intitule Ventes de planches à neige de la compagnie Super Glisse. L’axe horizontal correspond aux
années tandis que l’axe vertical, gradué de zéro à 180, correspond aux ventes en milliers de dollars.La bande de 2003,
en bleu marine, s’élève à 90. La bande de 2004, en rouge, s’élève à 110. La bande de 2005, en jaune, s’élève à 150. Et
la bande de 2006, en violet pâle, s’élève à 180.
Dans ce nouveau diagramme, puisque les longueurs des bandes sont proportionnelles aux ventes, on obtient un portrait plus juste des données. On voit maintenant mieux que les ventes n’ont pas doublé de 2004 à 2005 et on peut noter qu’elles ont presque doublé de 2003 à 2006.
Source : Guide d’enseignement efficace des mathématiques, de la 4e à la 6e année, p. 105-106.
