D2. Probabilité :
Décrire la probabilité que des événements se produisent et utiliser cette information pour faire des prédictions.
Situation d’apprentissage : on pige des cubes!
Durée totale : environ 2 heures
Déterminer et comparer les probabilités théoriques et expérimentales à l’aide d’événements indépendants et événements dépendants en pigeant des cubes d’un contenant au hasard.
| Attentes et contenus d'apprentissage |
|---|
|
Apprentissage socioémotionnel en mathématiques et processus mathématiques A1. Mettre en application, au mieux de ses capacités, diverses habiletés socioémotionnelles pour appuyer son utilisation des processus mathématiques et son apprentissage lié aux attentes et aux contenus d’apprentissage des cinq autres domaines d’étude du programme-cadre de mathématiques. Dans cette leçon, l’élève apprend, au mieux de ses capacités, à développer la conscience de soi et un sentiment d’identité personnelle et à penser de façon critique et créative en appliquant les processus mathématiques de réflexion (montrer qu’elle ou il prend le temps de réfléchir, tient compte des expériences antérieures et fait le suivi de ses réflexions pour aider à clarifier sa compréhension à mesure qu’elle ou il résout des problèmes) et de représentation (sélectionner et créer diverses représentations d’idées mathématiques et les appliquer à la résolution de problèmes) afin de se voir comme étant capable d’apprendre les mathématiques et de s’approprier son apprentissage, dans le cadre du développement de son sens de l’identité et de l’appartenance, et pouvoir établir des liens entre les mathématiques et des situations de la vie quotidienne pour être capable de former des opinions réfléchies et de prendre des décisions éclairées. Données D2. Décrire la probabilité que des événements se produisent et utiliser cette information pour faire des prédictions. D2.1 Décrire la différence entre des événements indépendants et des événements dépendants, et expliquer pourquoi leurs probabilités respectives diffèrent, en fournissant des exemples. D2.2 Déterminer et comparer les probabilités théoriques et expérimentales que deux événements indépendants se produisent et que deux événements dépendants se produisent. |
Présenter la situation suivante :
- Au moyen de deux différentes stratégies (dont l’une est le diagramme en arbre), représenter les probabilités théoriques des deux événements suivants :
- le premier cube est remis dans le contenant avant d’en tirer un autre (événements indépendants);
- le premier cube est conservé avant d’en tirer un autre (événements dépendants).
Voici quelques stratégies que peut utiliser l’élève pour résoudre le problème :
Stratégie 1 – Diagramme en arbre
J’énumère toutes les possibilités, à la suite de deux tirages consécutifs, dans un diagramme en arbre concernant les événements indépendants et les événements dépendants.
 Image « Indépendant, avec la remise. La probabilité de piger deux cubes rouges consécutifs
lorsque le premier est remis dans le contenant est de 9 sur 49 ou zéro virgule 184 ou 18 virgule 4 pourcent. » Le
diagramme en arbre présente les scénarios suivants. Si, à la première pige, on a « cube bleu deux probabilités sur
sept », et qu’à la deuxième pige, on a « cube bleu deux probabilités sur sept », le résultat est : cube bleu deux
probabilités sur sept multiplié par cube bleu deux probabilités sur sept égale quatre probabilités sur 49. Si à la
deuxième pige on a « cube rouge trois probabilités sur sept », le résultat est : cube bleu deux probabilités sur
sept multiplié par cube rouge trois probabilités sur sept égale six probabilités sur 49. Si à la deuxième pige on a
« cube vert deux probabilités sur sept », le résultat est : cube bleu deux probabilités sur sept multiplié par cube
vert deux probabilités sur sept égale 4 probabilités sur 49. Si, à la première pige, on a « cube rouge trois
probabilités sur sept », et qu’à la deuxième pige, on a « cube bleu deux probabilités sur sept », le résultat est :
cube rouge trois sur sept multiplié par cube bleu trois sur sept égale six probabilités sur 49.Si à la deuxième pige
on a « cube rouge trois probabilités sur sept », le résultat est : cube rouge trois probabilités sur sept multiplié
par cube rouge trois probabilités sur sept, égale 9 probabilités sur 49. Cette équation est la seule à être
surlignée de violet.Si à la deuxième pige on a « cube vert deux probabilités sur sept », le résultat est : cube
rouge trois probabilités sur sept multiplié par cube vert deux probabilités sur sept égale 6 probabilités sur 49.Si
à la première pige on a « cube vert deux probabilités sur sept », et qu’à la deuxième pige, on a « cube bleu deux
probabilités sur sept », le résultat est : cube vert deux probabilités sur sept multiplié par cube bleu deux
probabilités sur sept égale quatre probabilités sur 49. Si à la deuxième pige on a « cube rouge trois probabilités
sur sept », le résultat est : cube vert deux probabilités sur sept multiplié par cube rouge trois probabilités sur
sept égale six probabilités sur 49. Si à la deuxième pige on a « cube vert deux probabilités sur sept », le résultat
est : cube vert deux probabilités sur sept multiplié par cube vert deux probabilités sur sept égale quatre
probabilités sur 49.
Image « Indépendant, avec la remise. La probabilité de piger deux cubes rouges consécutifs
lorsque le premier est remis dans le contenant est de 9 sur 49 ou zéro virgule 184 ou 18 virgule 4 pourcent. » Le
diagramme en arbre présente les scénarios suivants. Si, à la première pige, on a « cube bleu deux probabilités sur
sept », et qu’à la deuxième pige, on a « cube bleu deux probabilités sur sept », le résultat est : cube bleu deux
probabilités sur sept multiplié par cube bleu deux probabilités sur sept égale quatre probabilités sur 49. Si à la
deuxième pige on a « cube rouge trois probabilités sur sept », le résultat est : cube bleu deux probabilités sur
sept multiplié par cube rouge trois probabilités sur sept égale six probabilités sur 49. Si à la deuxième pige on a
« cube vert deux probabilités sur sept », le résultat est : cube bleu deux probabilités sur sept multiplié par cube
vert deux probabilités sur sept égale 4 probabilités sur 49. Si, à la première pige, on a « cube rouge trois
probabilités sur sept », et qu’à la deuxième pige, on a « cube bleu deux probabilités sur sept », le résultat est :
cube rouge trois sur sept multiplié par cube bleu trois sur sept égale six probabilités sur 49.Si à la deuxième pige
on a « cube rouge trois probabilités sur sept », le résultat est : cube rouge trois probabilités sur sept multiplié
par cube rouge trois probabilités sur sept, égale 9 probabilités sur 49. Cette équation est la seule à être
surlignée de violet.Si à la deuxième pige on a « cube vert deux probabilités sur sept », le résultat est : cube
rouge trois probabilités sur sept multiplié par cube vert deux probabilités sur sept égale 6 probabilités sur 49.Si
à la première pige on a « cube vert deux probabilités sur sept », et qu’à la deuxième pige, on a « cube bleu deux
probabilités sur sept », le résultat est : cube vert deux probabilités sur sept multiplié par cube bleu deux
probabilités sur sept égale quatre probabilités sur 49. Si à la deuxième pige on a « cube rouge trois probabilités
sur sept », le résultat est : cube vert deux probabilités sur sept multiplié par cube rouge trois probabilités sur
sept égale six probabilités sur 49. Si à la deuxième pige on a « cube vert deux probabilités sur sept », le résultat
est : cube vert deux probabilités sur sept multiplié par cube vert deux probabilités sur sept égale quatre
probabilités sur 49.
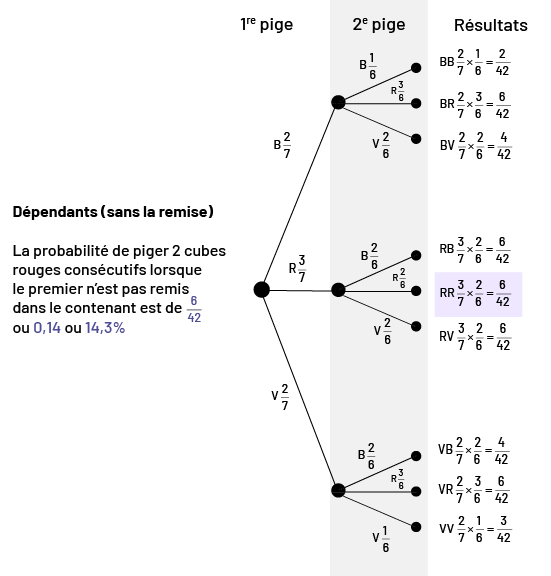 Image « Dépendant, sans la remise. La probabilité de piger deux cubes rouges consécutifs lorsque
le premier n’est pas remis dans le contenant est de six sur 42 ou zéro virgule 14 ou 14 virgule trois pourcent. » Le
diagramme en arbre présente les scénarios suivants. Si, à la première pige, on a « cube bleu deux probabilités sur
sept », et qu’à la deuxième pige, on a « cube bleu une probabilité sur six », le résultat est : cube bleu deux
probabilités sur sept multiplié par cube bleu une probabilité sur six égale deux probabilités sur 42. Si à la
deuxième pige on a « cube rouge trois probabilités sur six », le résultat est : cube bleu deux probabilités sur sept
multiplié par cube rouge trois probabilités sur six égale six probabilités sur 42. Si à la deuxième pige on a « cube
vert deux probabilités sur six », le résultat est : cube bleu deux probabilités sur sept multiplié par cube vert
deux probabilité sur six égale quatre probabilités sur 42. Si à la première pige on a « cube rouge trois
probabilités sur sept », et qu’à la deuxième pige, on a « cube bleu deux probabilités sur six », le résultat est :
cube rouge trois probabilités sur sept multiplié par cube bleu deux probabilités sur six égale six probabilités sur
42. Si à la deuxième pige on a « cube rouge deux probabilités sur six », le résultat est : cube rouge trois
probabilités sur sept multiplié par cube rouge deux probabilités sur six égale six probabilités sur 42. Ce résultat
est le seul à être surligné en violet. Si à la deuxième pige on a « cube vert deux probabilités sur six », le
résultat est : cube rouge trois probabilités sur sept multiplié par cube vert deux probabilités sur six égale six
probabilités sur 42. Si à la première pige on a « cube vert deux probabilités sur sept », et qu’à la deuxième pige
on a « cube bleu deux probabilité sur six », le résultat est : cube vert deux probabilités sur sept multiplié par
cube bleu deux probabilités sur six égale quatre probabilités sur 42. Si à la deuxième pige on a « cube rouge trois
probabilités sur six », le résultat est : cube vert deux probabilités sur sept multiplié par cube rouge trois
probabilités sur six égale six probabilités sur 42. Si à la deuxième pige on a « cube vert une probabilité sur six
», le résultat est : cube vert deux probabilités sur sept multiplié par cube vert une probabilité sur six égale
trois probabilités sur 42.
Image « Dépendant, sans la remise. La probabilité de piger deux cubes rouges consécutifs lorsque
le premier n’est pas remis dans le contenant est de six sur 42 ou zéro virgule 14 ou 14 virgule trois pourcent. » Le
diagramme en arbre présente les scénarios suivants. Si, à la première pige, on a « cube bleu deux probabilités sur
sept », et qu’à la deuxième pige, on a « cube bleu une probabilité sur six », le résultat est : cube bleu deux
probabilités sur sept multiplié par cube bleu une probabilité sur six égale deux probabilités sur 42. Si à la
deuxième pige on a « cube rouge trois probabilités sur six », le résultat est : cube bleu deux probabilités sur sept
multiplié par cube rouge trois probabilités sur six égale six probabilités sur 42. Si à la deuxième pige on a « cube
vert deux probabilités sur six », le résultat est : cube bleu deux probabilités sur sept multiplié par cube vert
deux probabilité sur six égale quatre probabilités sur 42. Si à la première pige on a « cube rouge trois
probabilités sur sept », et qu’à la deuxième pige, on a « cube bleu deux probabilités sur six », le résultat est :
cube rouge trois probabilités sur sept multiplié par cube bleu deux probabilités sur six égale six probabilités sur
42. Si à la deuxième pige on a « cube rouge deux probabilités sur six », le résultat est : cube rouge trois
probabilités sur sept multiplié par cube rouge deux probabilités sur six égale six probabilités sur 42. Ce résultat
est le seul à être surligné en violet. Si à la deuxième pige on a « cube vert deux probabilités sur six », le
résultat est : cube rouge trois probabilités sur sept multiplié par cube vert deux probabilités sur six égale six
probabilités sur 42. Si à la première pige on a « cube vert deux probabilités sur sept », et qu’à la deuxième pige
on a « cube bleu deux probabilité sur six », le résultat est : cube vert deux probabilités sur sept multiplié par
cube bleu deux probabilités sur six égale quatre probabilités sur 42. Si à la deuxième pige on a « cube rouge trois
probabilités sur six », le résultat est : cube vert deux probabilités sur sept multiplié par cube rouge trois
probabilités sur six égale six probabilités sur 42. Si à la deuxième pige on a « cube vert une probabilité sur six
», le résultat est : cube vert deux probabilités sur sept multiplié par cube vert une probabilité sur six égale
trois probabilités sur 42.
Stratégie 2 – Tableau des probabilités
J’énumère toutes les probabilités dans un tableau des probabilités.
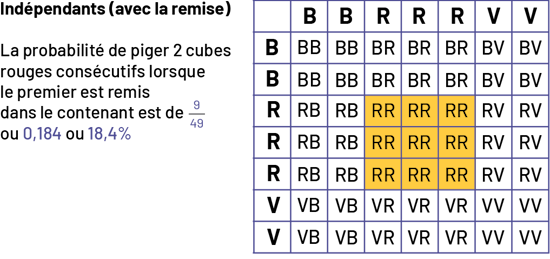 Image « Indépendant, avec la remise. La probabilité de piger deux cubes rouges consécutifs lorsque
le premier est remis dans le contenant est de 9 sur 40 ou zéro virgule 184 ou 18 virgule quatre pourcent. » Le
tableau illustre les combinaisons possibles en pigeant deux cubes lorsqu’on a dans un contenant deux cubes bleus,
trois cubes rouges et deux cubes verts. On utilise la première lettre de chaque couleur pour les nommer dans le
tableau : B, R et V. Les colonnes sont nommées comme suit : B, B, R, R, R, V, V. Les rangées sont nommées comme suit
: B, B, R, R, R, V, V. Chaque case de rencontre entre la rangée et la colonne inscrit les deux lettres
correspondantes. Les 9 cases où l’on retrouve la combinaison R R sont regroupées en plein centre du tableau
Image « Indépendant, avec la remise. La probabilité de piger deux cubes rouges consécutifs lorsque
le premier est remis dans le contenant est de 9 sur 40 ou zéro virgule 184 ou 18 virgule quatre pourcent. » Le
tableau illustre les combinaisons possibles en pigeant deux cubes lorsqu’on a dans un contenant deux cubes bleus,
trois cubes rouges et deux cubes verts. On utilise la première lettre de chaque couleur pour les nommer dans le
tableau : B, R et V. Les colonnes sont nommées comme suit : B, B, R, R, R, V, V. Les rangées sont nommées comme suit
: B, B, R, R, R, V, V. Chaque case de rencontre entre la rangée et la colonne inscrit les deux lettres
correspondantes. Les 9 cases où l’on retrouve la combinaison R R sont regroupées en plein centre du tableau
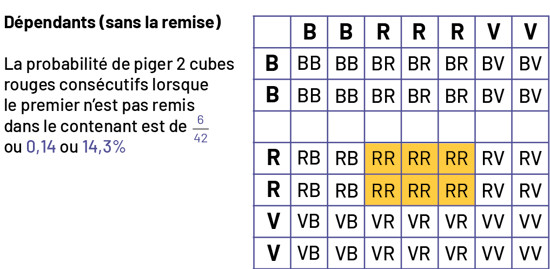 Image «
Dépendant, sans la remise. La probabilité de piger deux cubes rouges consécutifs lorsque le premier n’est pas remis
dans le contenant est de six sur 42 ou zéro virgule 14 ou 14 virgule trois pourcent. » Le tableau illustre les
combinaisons possibles en pigeant deux cubes lorsqu’on a dans un contenant deux cubes bleus, trois cubes rouges et
deux cubes verts. On utilise la première lettre de chaque couleur pour les nommer dans le tableau : B, R et V. Les
colonnes sont nommées comme suit : B, B, R, R, R, V, V. Les rangées sont nommées comme suit : B, B, R, R, V, V. La
troisième ligne du tableau est constituée de cases vides. Chaque case de rencontre entre la rangée et la colonne
inscrit les deux lettres correspondantes. Les six cases où l’on retrouve la combinaison R R sont regroupées vers le
centre du tableau, sous la rangée de cases vides.
Image «
Dépendant, sans la remise. La probabilité de piger deux cubes rouges consécutifs lorsque le premier n’est pas remis
dans le contenant est de six sur 42 ou zéro virgule 14 ou 14 virgule trois pourcent. » Le tableau illustre les
combinaisons possibles en pigeant deux cubes lorsqu’on a dans un contenant deux cubes bleus, trois cubes rouges et
deux cubes verts. On utilise la première lettre de chaque couleur pour les nommer dans le tableau : B, R et V. Les
colonnes sont nommées comme suit : B, B, R, R, R, V, V. Les rangées sont nommées comme suit : B, B, R, R, V, V. La
troisième ligne du tableau est constituée de cases vides. Chaque case de rencontre entre la rangée et la colonne
inscrit les deux lettres correspondantes. Les six cases où l’on retrouve la combinaison R R sont regroupées vers le
centre du tableau, sous la rangée de cases vides.
- Représente les probabilités expérimentales des deux événements à la suite de 10 essais, puis à la suite de 20 essais afin de les comparer avec les probabilités théoriques énumérées en a).
Stratégie
J’effectue maintenant les deux expériences (avec et sans la remise du premier cube dans le contenant) selon le nombre de fois demandées.
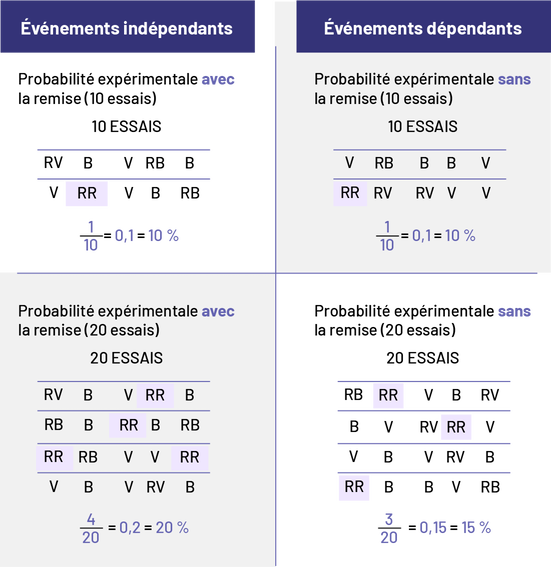 Image
Événements indépendants. Probabilité expérimentale avec la remise, dix essais. Première rangée : RV, B, V, RB, B.
Deuxième rangée : V, RR, B, RB. La combinaison RR est surligné en violet. Un sur dix égale zéro virgule un égale dix
pourcent. Événements dépendants. Probabilité expérimentale sans la remise, dix essais. Première rangée : V, RB, B, B,
V. Deuxième rangée : RR, RV, RV, V, V. La combinaison RR est surlignée en violet. Un sur dix égale zéro virgule un
égale dix pourcent.Probabilité expérimentale avec la remise, vingt essais. Première rangée. RV, B, V, RR. B. Deuxième
rangée : RB, B, RR, B, RB. Troisième rangée : RR, RB, V, V, RR. Quatrième rangée : V, B, V, RV, B. Toutes les
combinaisons RR sont surlignées en violet. Quatre sur vingt égale zéro virgule deux égale vingt pourcent. Probabilité
expérimentale sans la remise, vingt essais. Première rangée : RB, RR, V, B, RV. Deuxième rangée : B, V, RV, RR, V.
Troisième rangée : V, B, V, RV, B. Quatrième rangée : B, B, V, RB. Toutes les combinaisons RR sont surlignées en
violet. Trois sur vingt égale zéro virgule quinze égale quinze pourcent.
Image
Événements indépendants. Probabilité expérimentale avec la remise, dix essais. Première rangée : RV, B, V, RB, B.
Deuxième rangée : V, RR, B, RB. La combinaison RR est surligné en violet. Un sur dix égale zéro virgule un égale dix
pourcent. Événements dépendants. Probabilité expérimentale sans la remise, dix essais. Première rangée : V, RB, B, B,
V. Deuxième rangée : RR, RV, RV, V, V. La combinaison RR est surlignée en violet. Un sur dix égale zéro virgule un
égale dix pourcent.Probabilité expérimentale avec la remise, vingt essais. Première rangée. RV, B, V, RR. B. Deuxième
rangée : RB, B, RR, B, RB. Troisième rangée : RR, RB, V, V, RR. Quatrième rangée : V, B, V, RV, B. Toutes les
combinaisons RR sont surlignées en violet. Quatre sur vingt égale zéro virgule deux égale vingt pourcent. Probabilité
expérimentale sans la remise, vingt essais. Première rangée : RB, RR, V, B, RV. Deuxième rangée : B, V, RV, RR, V.
Troisième rangée : V, B, V, RV, B. Quatrième rangée : B, B, V, RB. Toutes les combinaisons RR sont surlignées en
violet. Trois sur vingt égale zéro virgule quinze égale quinze pourcent.
Dans les 10 essais, je ne vois pas de différence entre les probabilités expérimentales des événements indépendants et dépendants, même si, en théorie, je sais qu’il devrait y en avoir une. C’est une expérience, et les résultats sont aléatoires. Toutefois, je vois la différence entre les probabilités expérimentales des événements indépendants et dépendants lorsque je fais 20 essais. Avec plus d’essais, les résultats expérimentaux se rapprochent des probabilités théoriques.
Source : En avant, les maths!, 7e année, CM, Données, p. 4-8.
