D2.2 déterminer et comparer les probabilités théoriques et expérimentales que plusieurs événements indépendants se produisent et que plusieurs événements dépendants se produisent.
ACTIVITÉ 1 : ÉVÉNEMENTS INDÉPENDANTS
Les élèves de la 8e année cherchent à déterminer quelle équipe commencera avec le ballon lors de la prochaine joute de ballon-chasseur. Un élève propose alors de lancer trois dés à 4 faces pour déterminer l’équipe gagnante. L’équipe qui débutera la partie avec le ballon est celle qui obtiendra le plus grand nombre de points.
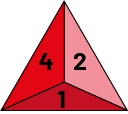
Sachant que l’équipe A a roulé un total de six points, quelle est la probabilité que l’équipe B :
- obtienne plus de points que l’équipe A?
- obtienne moins de points que l’équipe A?
- obtienne le même nombre de points que l’équipe A?
On s’intéresse à la probabilité des résultats combinés lorsqu’on lance les trois dés. Il faut d’abord déterminer et énumérer les résultats équiprobables possibles. Si le premier dé lancé s’arrête sur « 1 », le deuxième dé lancé peut s’arrêter sur «1 », «2 », «3» ou «4 ». Il en est de même pour le troisième dé lancé. Les mêmes combinaisons peuvent être représentées à l’aide d’un diagramme en arbre :
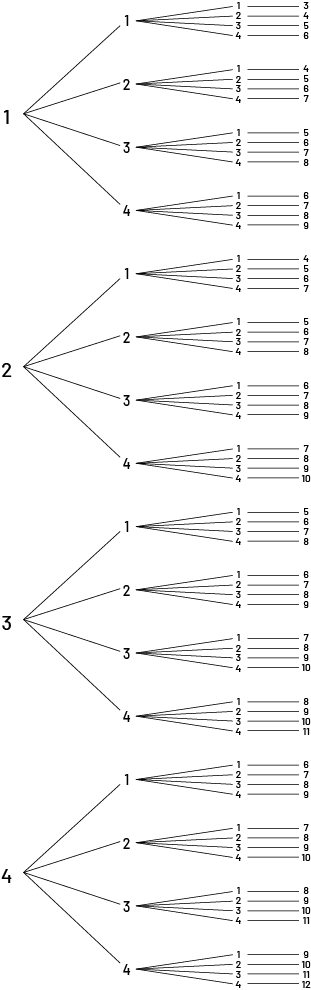image Le diagramme en arbre va comme suit. Les chiffres un à quatre sont placés l’un sous l’autre. À partir de chacun d’eux, quatre branches se déploient chiffrées respectivement un, deux, trois, quatre. À partir de chacune d’elles, quatre autres branches se déploient chiffrées respectivement un, deux, trois, quatre.Chacun des scénarios additionne ses chiffres. Un plus un plus un égale trois. Un plus un plus deux égale quatre. Un plus un plus trois égale cinq. Un plus un plus quatre égale six.Un plus deux plus un égale quatre. Un plus deux plus deux égale cinq. Un plus deux plus trois égale six. Un plus deux plus quatre égale sept.Un plus trois plus un égale cinq. Un plus trois plus deux égale six. Un plus trois plus trois égale sept. Un plus trois plus quatre égale huit.Un plus quatre plus un égale six. Un plus quatre plus deux égale sept. Un plus quatre plus trois égale huit. Un plus quatre plus quatre égale neuf.Deux plus un plus un égale quatre. Deux plus un plus deux égale cinq. Deux plus un plus trois égale six. Deux plus un plus quatre égale sept.Deux plus deux plus un égale cinq. Deux plus deux plus deux égale six. Deux plus deux plus trois égale sept. Deux plus deux plus quatre égale huit.Deux plus trois plus un égale six. Deux plus trois plus deux égale sept. Deux plus trois plus trois égale huit. Deux plus trois plus quatre égale neuf.Deux plus quatre plus un égale sept. Deux plus quatre plus deux égale huit. Deux plus quatre plus trois égale neuf. Deus plus quatre plus quatre égale dix.Trois plus un plus un égale cinq. Trois plus un plus deux égale six. Trois plus un plus trois égale sept. Trois plus un plus quatre égale huit.Trois plus deux plus un égale six. Trois plus deux plus deux égale sept. Trois plus deux plus trois égale huit. Trois plus deux plus quatre égale neuf.Trois plus trois plus un égale sept. Trois plus trois plus deux égale huit. Trois plus trois plus trois égale neuf. Trois plus trois plus quatre égale dix.Trois plus quatre plus un égale huit. Trois plus quatre plus deux égale neuf. Trois plus quatre plus trois égale 10. Trois plus quatre plus quatre égale onze.Quatre plus un plus un égale six. Quatre plus un plus deux égale sept. Quatre plus un plus trois égale huit. Quatre plus un plus quatre égale neuf.Quatre plus deux plus un égale sept. Quatre plus deux plus deux égale huit. Quatre plus deux plus trois égale neuf. Quatre plus deux plus quatre égale dix.Quatre plus trois plus un égale huit. Quatre plus trois plus deux égale neuf. Quatre plus trois plus trois égale dix. Quatre plus trois plus quatre égale onze.Quatre plus quatre plus un égale neuf. Quatre plus quatre plus deux égale dix. Quatre plus quatre plus trois égale onze. Quatre plus quatre plus quatre égale douze.
Inviter les élèves à remarquer qu’il y a un total de 64 résultats possibles.
Puisque l’équipe A a roulé six points, l’équipe B doit obtenir plus de six points si elle veut commencer la prochaine joute de ballon-chasseur avec le ballon. En analysant le diagramme en arbre ci-dessus, on remarque qu’il y a 44 possibilités d’obtenir plus de six points. La probabilité est donc égale à \(\frac{44}{64}\).
Toutefois, il y a 10 possibilités d’obtenir moins de six points. La probabilité que l’équipe B ne puisse guère commencer la joute de ballon-chasseur avec le ballon est donc égale à \(\frac{10}{64}\).
La probabilité que l'équipe B obtienne le même nombre de points que l’équipe A s’élève également à \(\frac{10}{64}\) puisqu’il y a 10 possibilités d’obtenir six points.
En analysant les probabilités théoriques, on remarque alors qu’il est très probable que ce soit l’équipe B qui débutera la partie avec le ballon lors de la prochaine joute de ballon-chasseur.
Afin de permettre la réalisation de la probabilité expérimentale, prévoir du matériel similaire pour effectuer l’expérience avec 100 essais dans la salle de classe. Si un dé à 4 faces n’est pas disponible, faire l’activité à partir d’un dé à 6 faces.
ACTIVITÉ 2 : ÉVÉNEMENTS DÉPENDANTS
Voici les cartes disponibles pour effectuer des piges lors d’un jeu de cartes :
Sachant que l’élève doit piger trois cartes les unes après les autres sans les remettre dans le paquet, quelle est la probabilité que l’élève obtienne:
- trois as (AAA)?
- un roi suivi de deux as?
- un roi parmi les trois cartes pigées?
Afin de déterminer l’ensemble des résultats possibles, les élèves peuvent utiliser un diagramme en arbre :
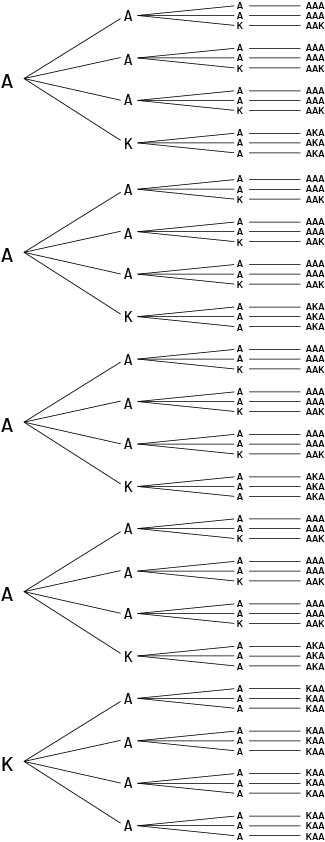image Le diagramme en arbre va comme suit. Quatre lettres « A » et une lettre « K », représentant quatre as et un roi, sont placées l’une sous l’autre. À partir de chacune d’elles, quatre branches se déploient avec les mêmes lettres : A, A, A, K. À partir de chacune d’elles, quatre autres branches se déploient avec encore les mêmes lettres : A, A, A, K.Chacun des scénarios crée un ensemble de lettres.
À partir de ces résultats, les élèves peuvent déterminer que la probabilité d’obtenir :
a) trois as est égale à \(\frac{24}{60}\);
b) un roi suivi de deux as est égale à \(\frac{12}{60}\);
c) un roi parmi les trois cartes est égale à \(\frac{36}{60}\).
Afin de permettre la réalisation de la probabilité expérimentale, prévoir du matériel similaire pour effectuer l’expérience avec 100 essais dans la salle de classe.